These movies show the evolution of chaos synchronization
in a system of coupled maps. In particular, the periodic
orbit structure of the following map is shown:
\(x -> cf(x),
y -> cf(x) + (1-c)g(y),
f(x) = a - x^2,
g(y) = b - y^2\).
In each case, \(x\) vs. \(y\) is plotted, and as the coupling is changed in time from \(c=0.5\) to \(0.0\). The yellow points depict the attractor, and the crosses are periodic orbits of periods 1-20 (cross colors refer to stability
properties). By design, the map exhibits identical sychronization for
\(c=1.0\). This persists (roughly for the nonidentical case) through
\(c=0.5\). As \(c\) is further decreased, bifurcations create additional
periodic orbits outside the original synchronziation manifold.
In the case of coupled identical maps, the "blowout bifucation,"
is immediately apparent as the attractor explodes to include
these additional orbits. For the case of coupled nonidentical
maps, this transition is is more gradual.
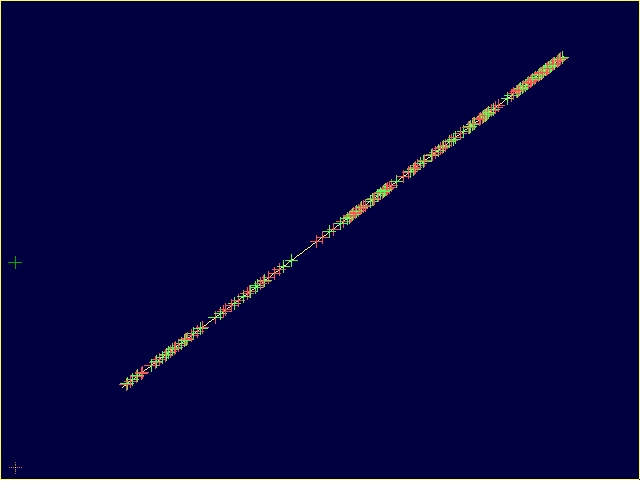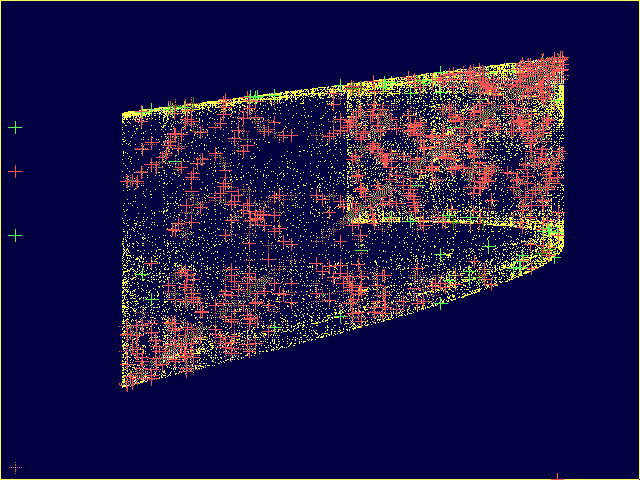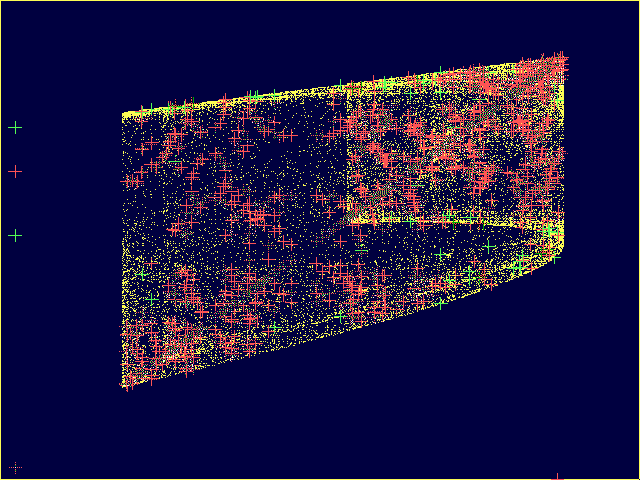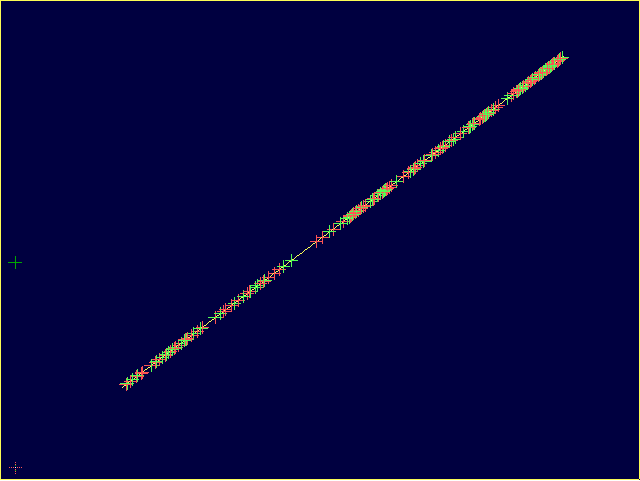
Coupled Identical Maps: \((a, b)=(1.7, 1.7)\).

Coupled Nonidentical Maps: \((a, b)=(1.9, 1.45)\).
| Author Institutional Affiliation | Dept. of Physics & Astronomy, Krasnow Institute for Advanced Study George Mason University |
| Author Email | |
| Author Postal Mail | Mail Stop 2A1 George Mason University Fairfax, VA 22030 USA Tel.: (703) 993-4431 |
| Keywords | Chaos, Synchronization, Coupled Maps |