If all the components of a metal alloy are heated to a high enough
temperature, they will quickly form an almost perfect homogeneous
mixture. If this mixture is then rapidly quenched below a certain
temperature, the solution solidifies. Depending on the concentrations
of the involved metals, different processes of phase separation may
set in. During a process called spinodal decomposition, the components
immediately start to separate again, thereby forming a highly
inhomogeneous fine-grained structure exhibiting a characteristic
length scale. Depending on the relative concentrations of the
involved metals, one can observe connected snake-like patterns, or
disconnected patterns. The included pictures and movies show the
decomposition process and observed patterns for a binary alloy, i.e.,
an alloy consisting of two metals. The underlying mathematical model
is the Cahn-Hilliard partial differential equation.

Pattern in 2D, equal mass: A sample pattern observed on a square domain. The two involved components have equal mass.

Pattern in 2D, different mass: A sample pattern observed on a square domain. The two involved components have different mass.
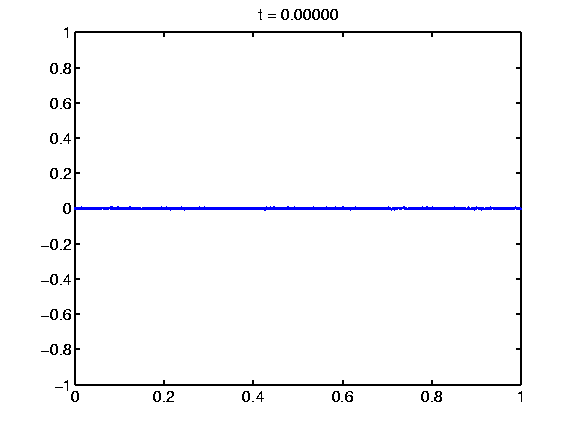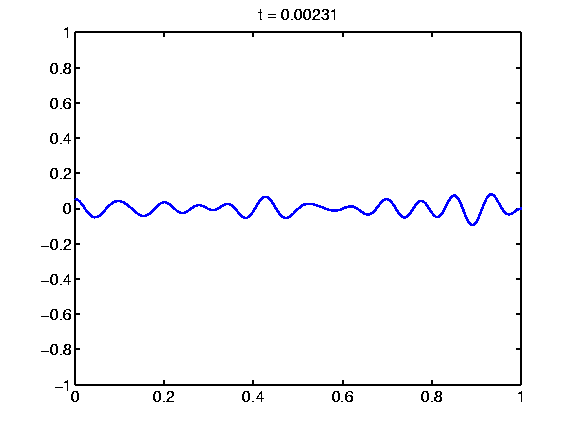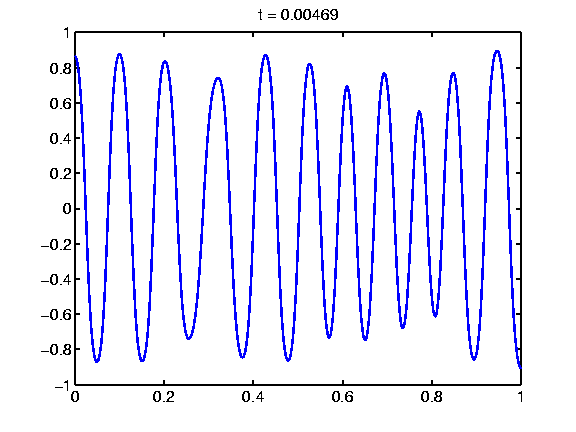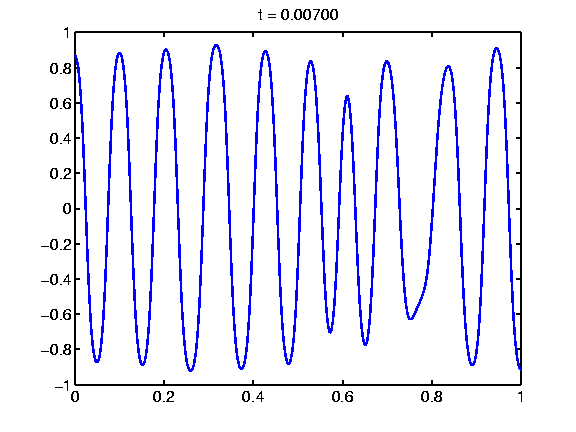
Evolution in 1D, equal mass: A sample decomposition movie observed for a 1D domain. The two involved components have equal mass.
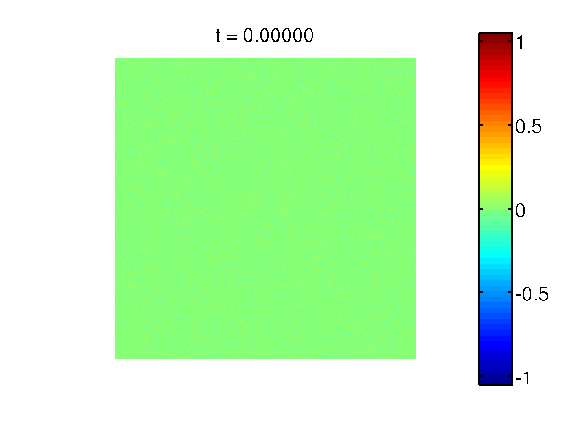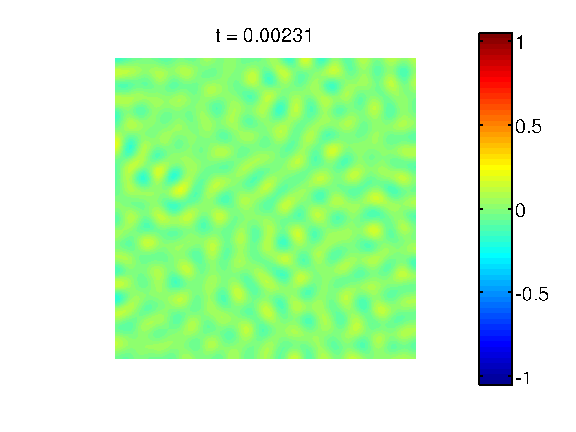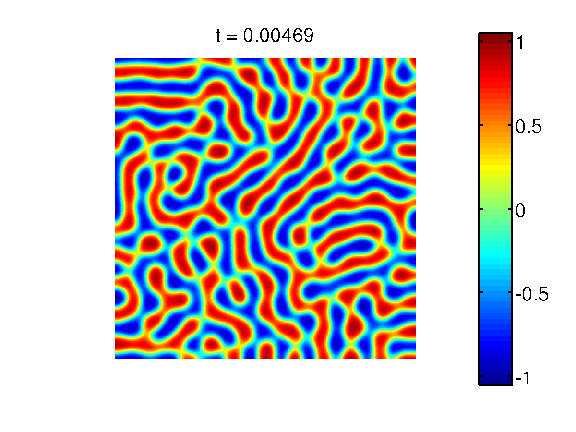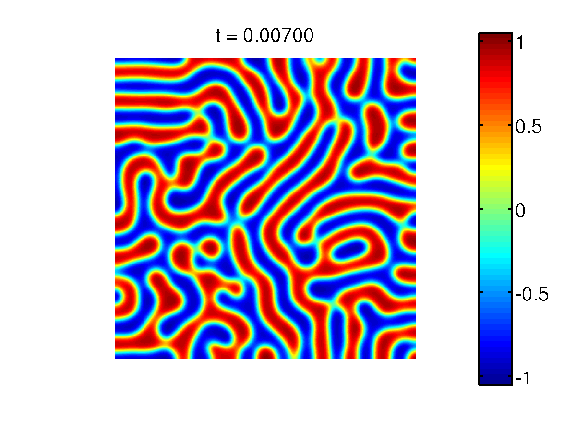
Evolution in 2D, equal mass: A sample decomposition movie observed on a square domain. The two involved components have equal mass.
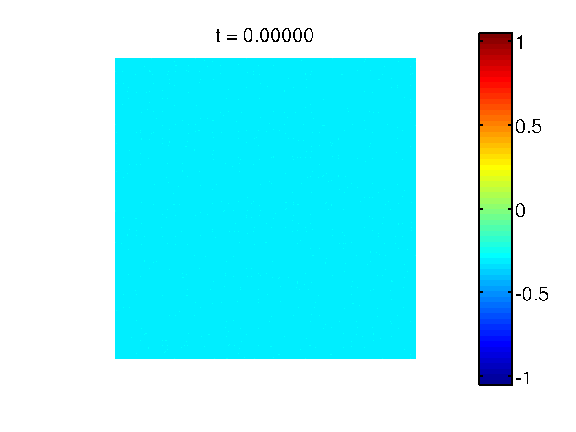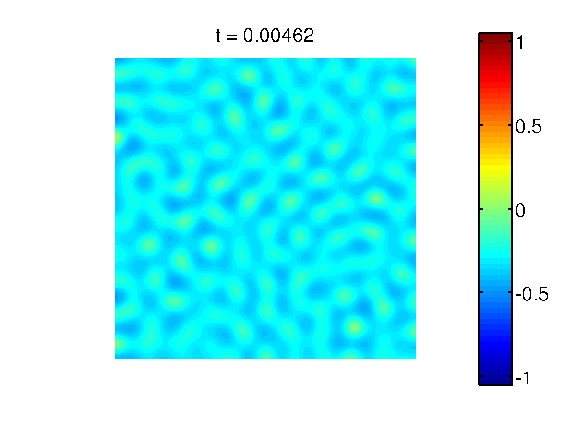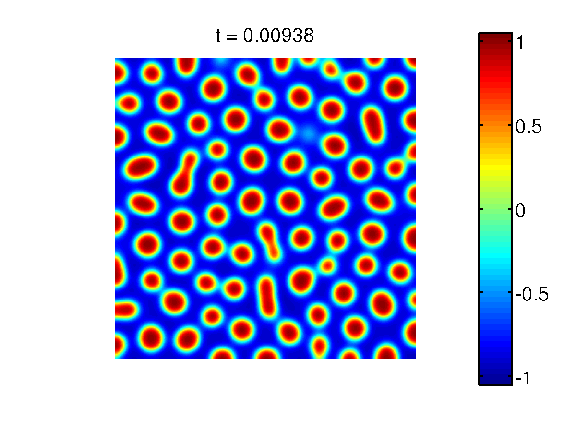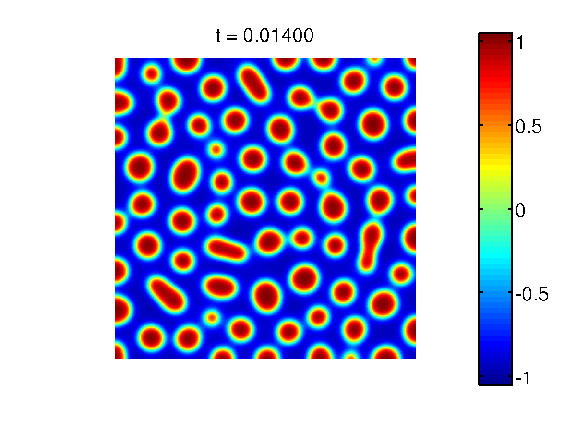
Evolution in 2D, different mass: A sample decomposition movie observed on a square domain. The two involved components have different mass.
| Author Institutional Affiliation | George Mason University |
| Author Email | |
| Author Postal Mail | Department of Mathematical Sciences George Mason University, MS 3F2 Fairfax, VA 22030 |
| Notes | Based on joint work with Stanislaus Maier-Paape and Evelyn Sander. |
| Keywords | Spinodal decomposition, Cahn-Hilliard equation |