A recent article in Chaos [Barreto et al., Chaos, 13(1):151-164, 2003] describes a drive-response system coupling a parametrized family of noninvertible modified baker maps with a nonlinear response. The article describes the effect of noninvertibility on the synchronization set (i.e. the attractor). Namely, at the bifurcation parameter, the synchronization set has a cusp. For every parameter after the bifurcation, there is a
multivalued synchronization set with self-intersections, or loops.
See the first animation. This example is a special case in which the
noninvertibility occurs at a critical point of the synchronization
set. In contrast, the synchronization set generically continues to be
a smooth nonintersecting curve even after the onset of
noninvertibility. See Animations 2 and 3. This is described more
fully in an upcoming article by Josic and Sander.
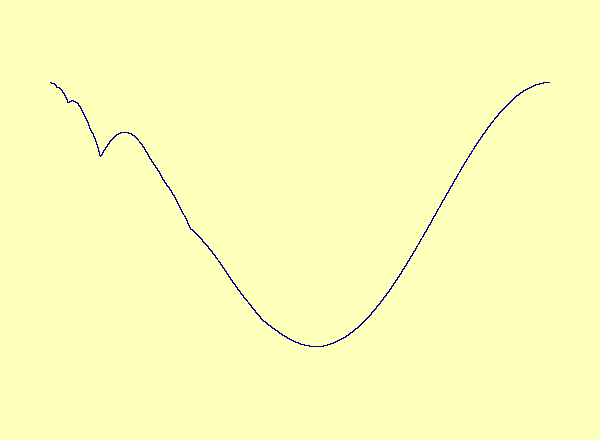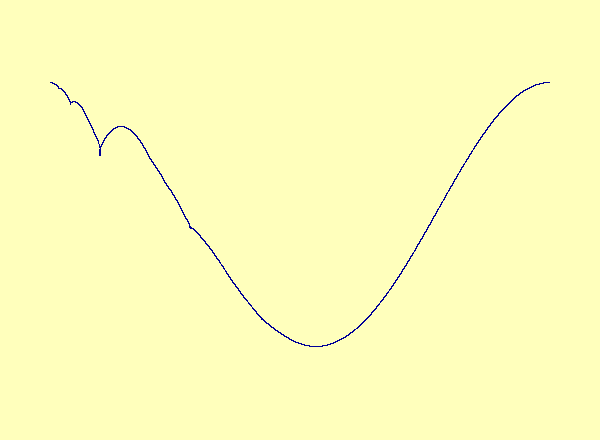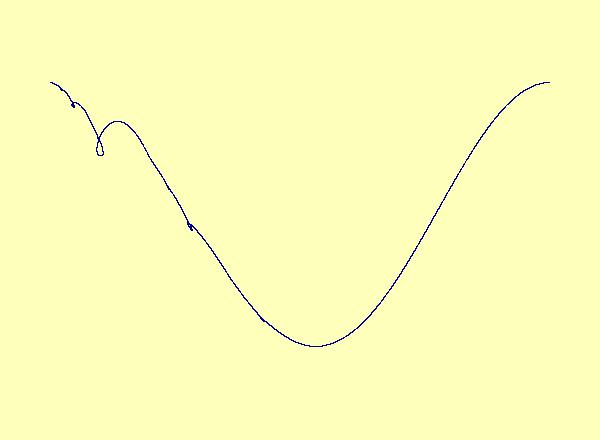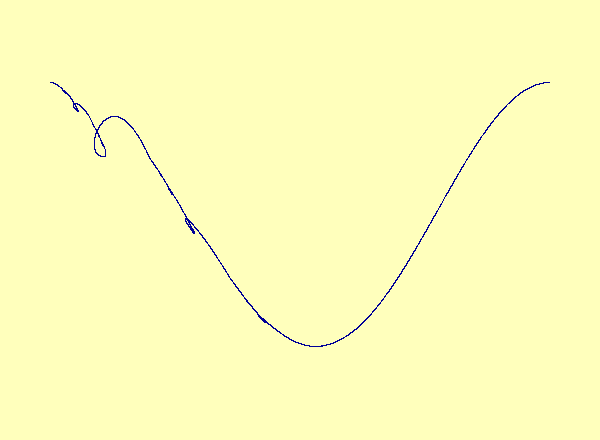
\(u\) versus \(y\) in the exceptional case of Barreto et al. As the parameter varies, a smooth manifold forms a cusp, which turns into a loop.
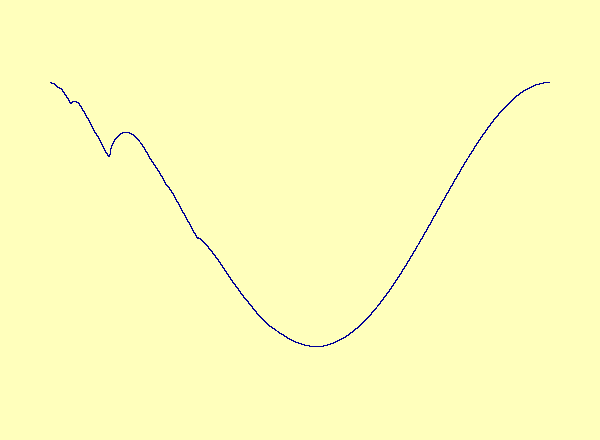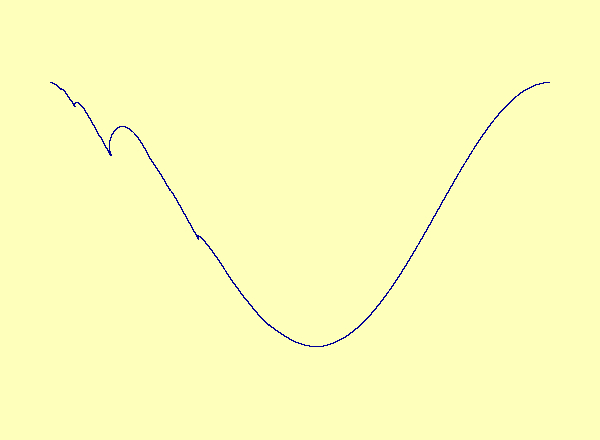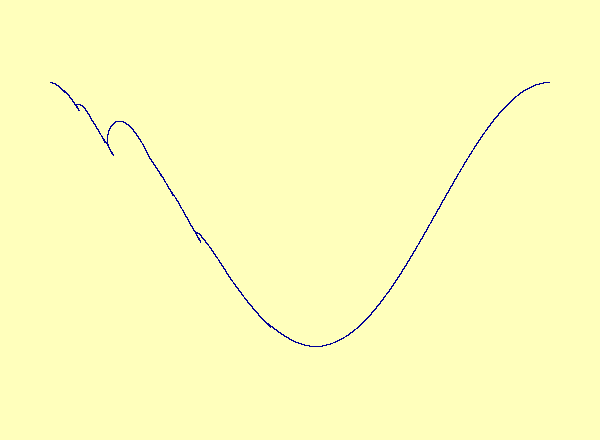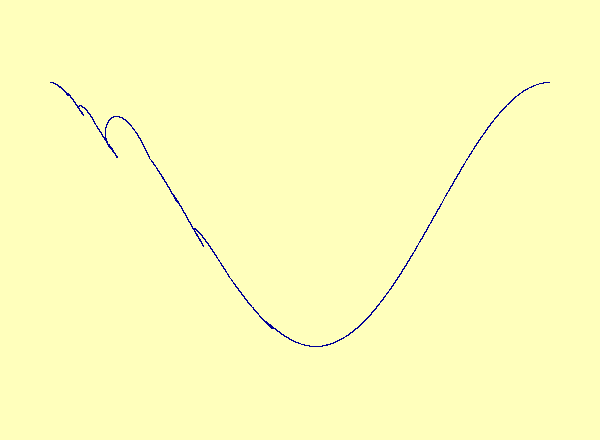
\(u\) versus \(y\) in the typical case; the noninvertibility does not occur at a critical point. Therefore the synchronization set becomes multivalued as a graph but retains its smooth manifold structure.
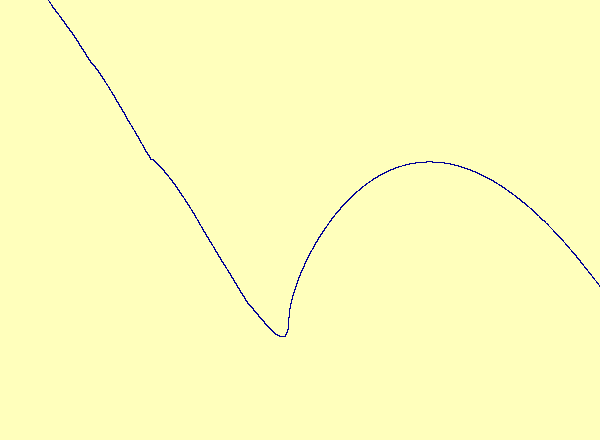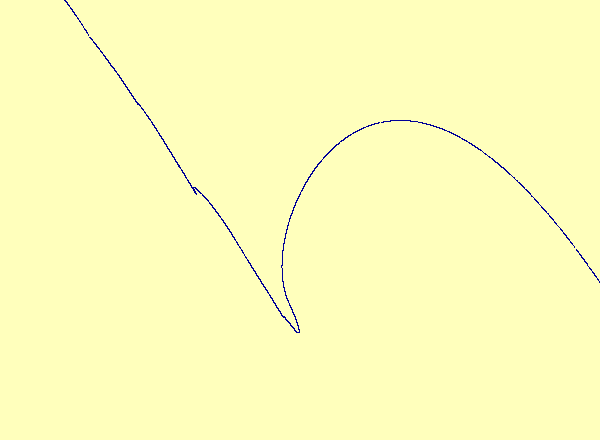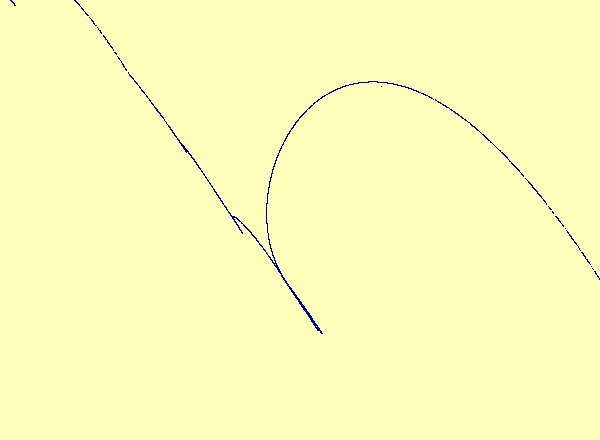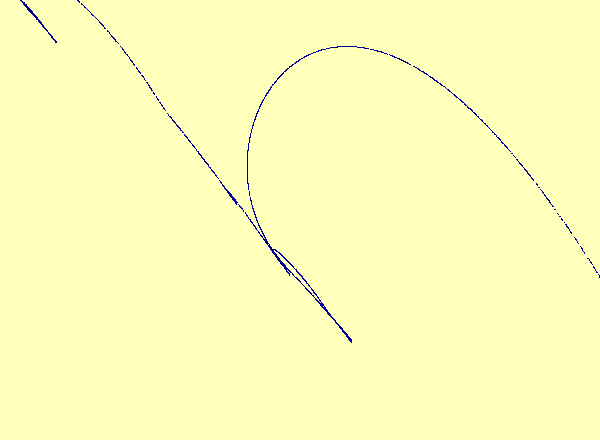
A closeup view of the main loop in the previous animation.
| Author Institutional Affiliation | George Mason University, University of Houston |
| Author Email | |
| Author Postal Mail | Department of Mathematical Sciences, George Mason University, 4400 University Drive, MS 3F2, Fairfax, VA 22030 |
| Keywords | drive-response system, synchronization |