Golden mean orchid in a generalized Harper equation: The special case of the discrete Schrödinger equation known as the Harper equation (also known as the almost Mathieu equation) is important in studying the localization transition in incommensurate systems. In the strong coupling regime the exponentially localized eigenstates possess universal self-similar fluctuations. Renormalization explains these fluctuations, and we now have a rigorous description of the existence and properties of the underlying golden mean renormalization operator, its fixed point, and strange set - Ketoja-Satija orchid - occuring in a generalised Harper equation. Mathematically this description boils down to a detailed analysis of a particular functional recurrence. In a generalised Harper equation which includes the effect of next-nearest neighbour interactions, the strong-coupling regime is characterised by a universal strange attractor (the Ketoja-Satija Orchid) for the recurrence.
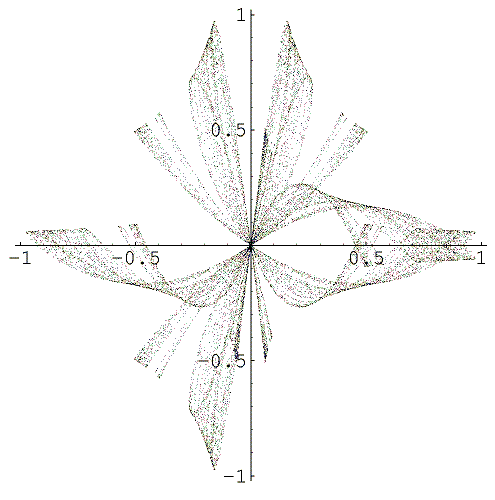
In a generalised Harper equation which includes the effect of next-nearest neighbour interactions the strong-coupling regime is characterised by a universal strange attractor called the Ketoja-Satija Orchid.
| Author Institutional Affiliation | University of Portsmouth |
| Author Email | |
| Notes | References: J. A. Ketoja and I. I. Satija, Phys. Rev. Lett. 75 (1995), 2762-2765.
B. D. Mestel and A. H. Osbaldestin, J. Math. Phys. 45 (2004) 5042-5075. |
| Keywords | Renormalisation, Golden Mean, Functional Recurrence, Strange Set, Harper Equation |