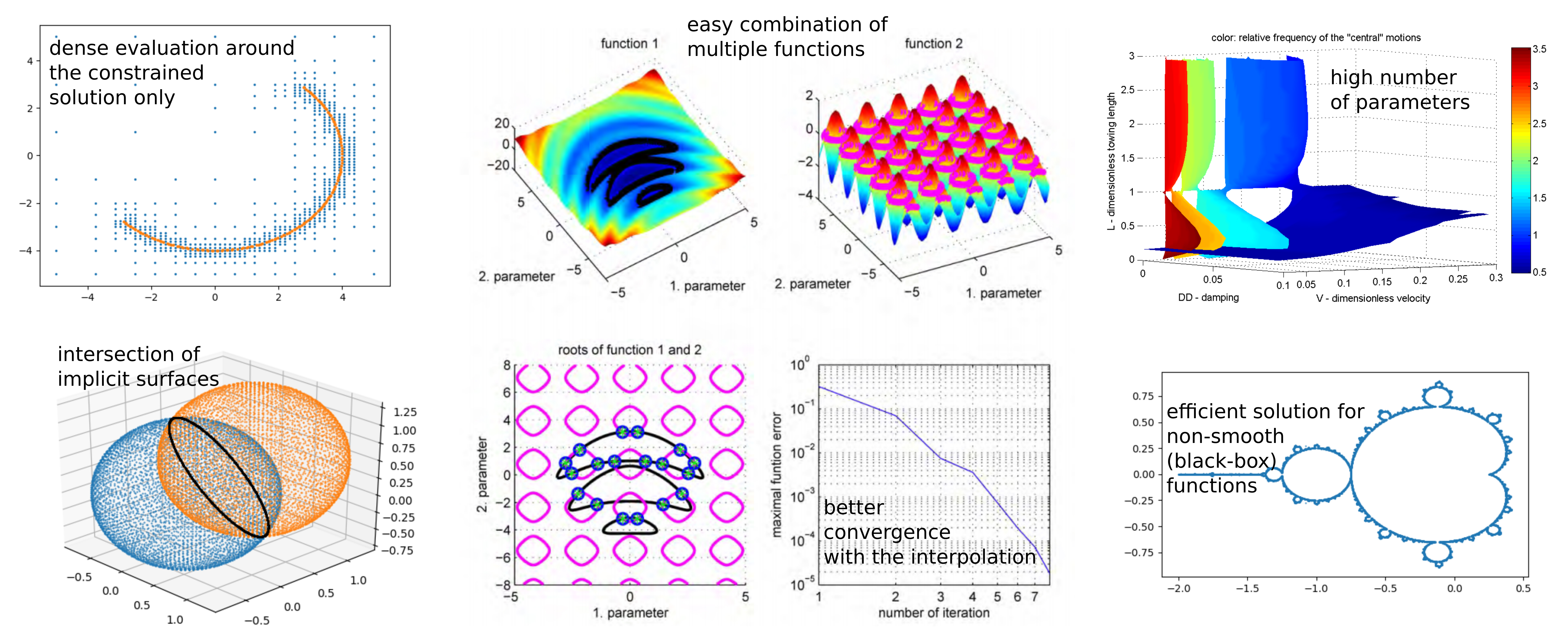
Overview
Multi-Dimensional Bisection Method (MDBM) is an efficient and robust root-finding algorithm, which can be
used to determine whole high-dimensional submanifolds (points, curves, surfaces…) of the roots of implicit
non-linear equation systems, even in cases, where the number of unknowns surpasses the number of
equations.
\(fi(x_j)=0 \quad i=1...k \quad j=1...l, \quad k \leq l\)
This method is an alternative to the contour plot or to isosurfaces in higher dimension, however, it has as the
advantage of being able to handle multiple functions at once.
In addition, it uses far less function evaluation than the brute-force approach, making it much faster and more
memory efficient, especially for complex tasks.
Currently a Matlab package and a Julia package is available:
Introduction
The bisection method—or the so-called interval halving method—is one of the simplest root-finding algorithms
which is used to find zeros of continuous non-linear functions. This method is very robust and it always tends
to the solution if the signs of the function values are different at the borders of the chosen initial interval.
Geometrically, root-finding algorithms of \(f(x)=0\) find one intersection point of the graph of the function with the
axis of the independent variable. In many applications, this 1-dimensional intersection problem must be
extended to higher dimensions, e.g.: intersections of surfaces in a 3D space (volume), which can be
described as a system on non-linear implicit equations. In higher dimensions, the existence of multiple
solutions becomes very important, since the intersection of two surfaces can create multiple intersection
curves.
MDBM algorithm can handle automatically:
- multiple solutions
- arbitrary number of parameters (typically: 3-6)
- arbitrary number implicit equations
- constraints in the parameter space
- handle degenerated functions
- first and second order interpolation (and convergence rate)
- provides the gradients of the equations for the roots
- refinement the selected region only
- interpolation for higher resolution plotting
Motivation: Compute the stability chart of a Dynamical System
During my studies and research, I have to determine stability charts of models described by delayed
differential equations, which are typically formed as a "2 implicit equation / 3 parameter" problem. The two
equations are related to the real and imaginary part of the characteristic equation. Two parameters determine
the stability chart and the third parameter is the vibration frequency (of the trial function).
I have faced the difficulty that there is no applicable solution in any available software (e.g.: Mathematica,
Matlab,...) which could easily be used in engineering problems. The continuation method in a bifurcation
analysis could be a good solution, however, it is not automatic, requires considerable human interaction, and fails to find
closed curves. Due to this reason, I have started to develop the Multi-Dimensional Bisection Method in 2006
in Matlab, and I have been improving it since, by adding new features from time to time. The combination of
the MDBM with the Semi-Discretization method, Multi-Frequency solution of other spectral methods can lead
to an efficient stability chart calculation.
Further more, higher dimensional rooth-finding problems can be found in many different field of science, just
to mention a few published application the the MDBM:
- stability chart computation
- stabilizability diagram
- robust stability calculation
- differential geometry (isolines, isosurfaces in higher dimensions)
- analysis of linkages (mechanical: workspace of robots)
Citing
The software in this ecosystem was developed as part of academic research. If you use the MDBM.jl
package as part of your research, teaching, or other work, I would be grateful if you could cite my
corresponding publication: https://pp.bme.hu/me/article/view/1236/640
Bachrathy Dániel, Stépán Gábor, Bisection method in higher dimensions and the efficiency number.
PERIODICA POLYTECHNICA-MECHANICAL ENGINEERING 56:(2) pp. 81-86. (2012) DOI:
10.3311/pp.me.2012-2.01
| Model | |
| Software Type | |
| Language | |
| Platform | |
| Availability | Currently a Matlab package and a Julia package is available:
|
| Contact Person | |
| References to Papers | The software in this ecosystem was developed as part of academic research. If you use the MDBM.jl
package as part of your research, teaching, or other work, I would be grateful if you could cite my
corresponding publication: https://pp.bme.hu/me/article/view/1236/640
Bachrathy Dániel, Stépán Gábor, Bisection method in higher dimensions and the efficiency number.
PERIODICA POLYTECHNICA-MECHANICAL ENGINEERING 56:(2) pp. 81-86. (2012) DOI:
10.3311/pp.me.2012-2.01 |