One-Dimensional Strong Stable and Unstable Manifolds
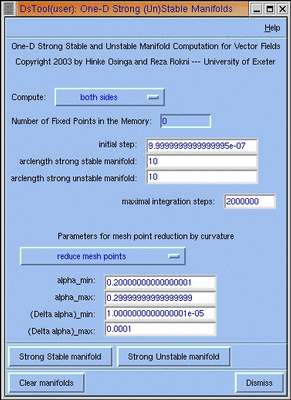
SSMan1D is a software package for one-dimensional strong (un)stable manifold computation that can be linked to the Tcl/Tk version of DsTool
When downloading the Strong (Un)Stable Manifold 1D code, please see the Readme file for instructions. Then download:
SSMan1D.tgz (15Kb)
Motivation for SSMan1D
The motivation for writing the Strong (Un)Stable Manifold 1D code comes from Control Theory. When using adaptive control, the system typically transforms into a dynamical system that has amanifold of equilibria. Hence, all these equilibria are non-hyperbolic. With this kind of control design it is important to understand the qualitative behaviour of the adaptive system, and in particular the asymptotic stability properties. In other words, one is interested in the geometry of the strong stable and unstable manifolds of these non-hyperbolic equilibria.
DsTool offers the possibility to compute equilibria of a vector field and the associated one-dimensional stable and unstable manifolds if the equilibria are hyperbolic. However, the algorithm that is used is not restricted to hyperbolic equilibria. Since a non-hyperbolic equilibrium can still have well-defined one-dimensional strong stable or unstable manifolds, SSMan1D was designed to compute and visualise them in the DsTool environment.
The Strong (Un)Stable Manifold 1D code computes one-dimensional strong stable and unstable manifolds of both hyperbolic and non-hyperbolic equilibria up to a pre-specified arclength. The extension module uses the algorithm of DsTool to compute the manifolds, but then reduces the number of points to represent the manifold using curvature accuracy conditions.
| Keywords | Dynamics (phase diagrams), Visualization |
| Model | |
| Software Type | |
| Language | |
| Platform | |
| Availability | |
| Contact Person | |
| References to Papers |
- H.M. Osinga and G.R. Rokni Lamooki (2003)
"Numerical study of manifold computations"
to appear in Proceedings of the International Conference on Differential Equations, Equadiff 2003.
- H.M. Osinga, G.R. Rokni Lamooki, and Stuart Townley (2004)
"Numerical approximations of strong (un)stable manifolds"
to appear in Dynamical Systems.
|