Dynamical Systems in Jet Engines: A Symmetry-Based Approach

by
Prashant G. Mehta Department of Mechanical & Industrial Engineering University of Illinois at Urbana-Champaign 1206 W. Green Street Urbana, IL 61801 [email protected]	Gregory Hagen Components Department United Technologies Research Center 411 Silver Lane East Hartford, CT 06040 [email protected]	Andrzej Banaszuk Systems Department United Technologies Research Center 411 Silver Lane East Hartford, CT 06040 [email protected]

		Jet engines are among the most complex systems, with part counts ranging in the thousands, engineered by specialists drawn from diverse core disciplines such as fluid dynamics, combustion, acoustics, structures, and materials. Advanced diagnostics and automatic control serve to maximize performance and ensure stability in the engines. Static descriptors, such as part counts, form the typical metrics of complexity in these systems. However, there is another kind of complexity pertaining to the range of non-equilibrium dynamic phenomena, turbulence being only one of the many observed.
United Technologies Research Center

Given the parameter regimes of the physics, e.g. very high Reynolds numbers, it is perhaps not surprising to the Dynamical Systems community that the behavior is very rich dynamically. It may, however, come as a bit of a surprise that some of the non-equilibrium unsteady behavior is non-detrimental, even desirable. An example is the turbulent mixing that is critical for combustion. Nevertheless, a lot of the dynamic behavior, typically deemed instabilities, is detrimental. Examples include combustion instabilities leading to structural damage, turbulent jet noise leading to environmental noise pollution, structural vibrations leading to fan blade fatigue and fracture, and flow separation and instabilities leading to compressor surge and stall.

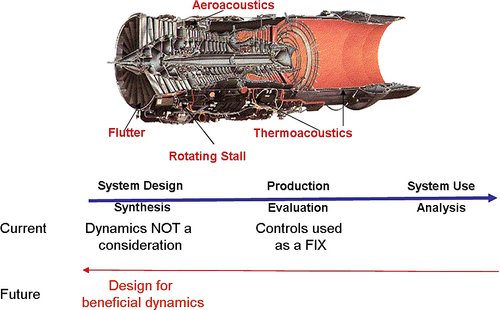Figure 1: Current and future strategies for tackling instability problems in a jet engine

Jet engines are high-energy devices and the effects of these instabilities range from reduced performance to catastrophic engine damage. A number of NASA films from the sixties show rocket engines exploding on test stands, testifying to the potential perils of combustion instabilities. Current fixes include
a)	operating in design space where these instabilities are mild,
b)	using diagnostics such as monitoring for blade fatigue,
c)	passive fixes such as weighty liners that serve to dissipate acoustic energy in the case of combustion instability, and
d)	some active feedback control approaches.
The passive approaches are at best a 'band-aid' on the problem, and come with increased weight and cost, and decreased performance. Active control approaches require accurate models for controller design, and most importantly suffer from fundamental performance limitations due to physical factors such as delay, actuator bandwidth, etc.
			East Hartford

The fundamental problem here is that while the engine is designed to be optimal with respect to the static performance metrics, it is not designed so with respect to any dynamical behavior that may arise. For example, even though combustion in a confined engine cavity is good for thrust, the feedback coupling between resonant acoustic modes of the cavity and heat released due to combustion can lead to undesirable thermo-acoustic oscillations. What is needed is a design approach that integrates the design of dynamics together with other design objectives.

Figure 2: Schematic of an interconnected system where a wave equation is in feedback with a dynamic model

Two key technical barriers to analysis and design of dynamics are

1. the complexity of the observed phenomenon, and
2. the lack of suitable models.

This motivates our approach to utilize the structure in the problem, namely its equivariance or symmetry properties. In the remainder of this article, we outline some key ideas with the aid of a wave equation on a circle in feedback with a dynamic model, of which only the structure is assumed to be known. Figure 2 depicts the schematic of the interconnection. Examples of wave phenomena in jet engines include both acoustics and structures. Feedback may arise as a result of combustion, leading to combustion instability, or from fluid dynamics, leading to blade flutter. Even though the observed instability phenomenon is robust and large scale, the feedback models are generally very complex with spatio-temporal uncertain dynamics on multiple scales. Traditional approaches approximate these complex feedback models with either very coarse models such as lumped delay, or with very fine-scale CFD descriptions, which are not amenable to analysis or design.

Our approach, in contrast, is not to focus on the precise dynamics of the feedback model, but to work instead with its structural properties, such as symmetry. Our two main ideas are:

1. the structure of the feedback can be used to explain the instability, and
2. manipulation of the structure can be used to control the instability.

These ideas are almost without precedents in the aerospace research community. After all, it is difficult to imagine symmetry in engines. However, these ideas have been applied successfully to

a)	develop a set of computational tools to identify and analyze time-series instability data from experiments, and
b)	design changes on one of the engines.

The mathematics of these ideas is outlined below.

The first idea, based on methods of equivariant bifurcation theory, is to use only the symmetry properties of the feedback model in Fig. 2 to explain the instability. The wave equation has the so-called spatial symmetry group O(2), whereby the partial differential equation is equivariant with respect to rotations and reflections. As a result of this, the individual eigenvalues are double. Moreover, because of physical consideration, these eigenvalues are lightly damped and close to the imaginary axis. The double eigenvalues correspond to the fact that a clockwise-rotating eigenmode is accompanied by its counter-clockwise-rotating symmetric counterpart. The instability phenomenon is related to the migration of one of these eigenvalues into the right half complex plane because of the dynamics of the feedback model.

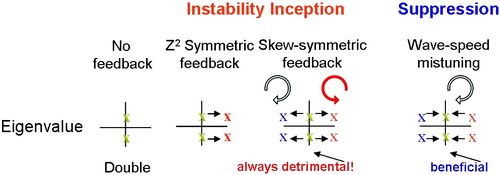Figure 3: The different types of impact that symmetric and skew-symmetric heat release feedbacks have on double eigenvalues of the acoustics.

To derive results on stability, we showed that under the assumption of identical feedback elements (identical combustion flameholders, identical fan blades, etc.), any feedback model can be decomposed as a sum of symmetric and a skew-symmetric feedback. Conceptually, the symmetric feedback corresponds to dynamics that have reflection (about centerline) symmetry while the skew-symmetry is a result of local asymmetry in feedback. Figure 3 shows the impact of symmetric and skew-symmetric heat release feedbacks on any double eigenvalues of the acoustics. The symmetric feedback causes the two eigenvalues to move as a pair in the same direction. It can either stabilize or de-stabilize depending upon the feedback model. The skew-symmetric feedback, on the other hand, is always detrimental regardless of the feedback model. It splits the eigenvalues, causing one rotating mode to gain damping while the other rotating mode loses the same amount of damping. Using only the time-series data from experiments, the instability seen in experiments can be explained as a consequence of the skew-symmetric feedback.

The second idea is to modify the structural aspects of the model in order to control the instability. This can be accomplished by introducing precise spatial variations (mistuning) in the "mean properties" such as wave speed of the wave equation. While the skew-symmetric feedback causes the two eigenvalues to move apart, mistuning causes the eigenvalues to move closer as shown in Fig. 3. In either case, the net amount of damping in the system remains the same. This net damping depends upon the net symmetric feedback due to the presence of liner etc. and is not affected by spatial variation in mean. In effect, the mistuning utilizes the more heavily damped system modes to augment the damping of the lightly damped modes.

		For a given skew-symmetric feedback (split of eigenvalues), there is an optimal amount of mean variations that reverses the detrimental effect of skew-symmetric feedback. This optimal amount corresponds to the eigenvalue diagram where the nominally double eigenvalues are the closest. Decreasing the amount of mistuning from the optimal amount causes one of the modes to become more damped at the expense of the other mode, which becomes less damped. On the other hand, increasing the mistuning beyond the optimal amount causes the frequencies of the two counter-rotating modes to shift without any additional damping augmentation.
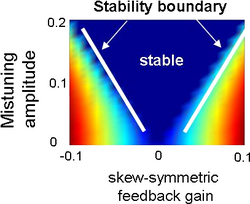
Figure 4: Model-independent stability boundary as a function of skew-symmetry and mistuning.

The innovation lies in using only the symmetry structure of the feedback model to carry out both the analysis of the instability and design for its suppression. Skew-symmetry in feedback gives feedback model-independent conclusion on stability, while mistuning of the mean properties yields model-independent control of the instability. Figure 4 shows a model-independent stability boundary as a function of skew-symmetry and mistuning. The optimal pattern for the mistuning is related to the dynamics of the wave operator. However, one can show that the conclusions are robust with respect to mistuning characteristics.

Validity of the analysis and design ideas can be demonstrated in full scale devices. These ideas borrow heavily from Dynamical Systems concepts, and result in a paradigm shift in both the analysis of instability and the design for instability mitigation in a class of jet engines. The success story highlights the role that the Dynamical Systems community can play in analysis and design of complex engineered systems such as jet engines. It is our sincere belief that the results summarized in this article only reflect the tip of the iceberg and "Design of Dynamics" will come to play an ever-increasing role in the complex systems of the future.
		Connecticut around Halloween