Sofia H. Piltz, May the Piecewise-Smooth, Smooth, and Slow-Fast Plankton be with You.

I am an applied mathematician with enthusiasm in bridging the fields of mathematics and biology via ordinary differential equation models. Below, I give an expository account of my doctoral work and its follow-up, namely, on developing piecewise-smooth, smooth, and slow-fast models for plankton population dynamics and comparing them to each other. I did my PhD in the Life Sciences Interface Doctoral Training Centre at the University of Oxford, UK. After finishing my degree, I continued developing models for plankton blooms as a postdoctoral fellow at the Technical University of Denmark. Currently, I'm a postdoctoral assistant professor at the University of Michigan where I apply mathematiconal models to human sleep and wake cycles.

I chose to do a PhD project on plankton population dynamics based on my childhood interest in marine mammals. Due to unexpected circumstances, my decision had to be made in a short time and there was no previous work upon which the project would have been easily built. Luckily, my choice turned out to be an intriguing example of using different kinds of differential equation models to gain biological insight -- which was exactly what I wanted to do, and continues to keep me intrigued and busy even after finishing my PhD.

During the first year, I obtained access to an observational data set including measurements of population densities of ciliates, i.e., eukaryotic single cells with animal-like behavior, and their algal prey in Lake Constance on the German-Swiss-Austrian border. As subgroups of plankton, these organisms are an important link between the bottom and higher levels of the aquatic food chain. Because of their large population size, short lifespan, and small size, the ciliate-algae predator-prey system serves as an excellent model for other complex (eco)systems. In addition, these organisms are often found in the well-mixed upper part of the water column, which makes the use of ordinary differential equations well-founded.

My PhD research question was inspired by earlier studies of ciliates in Lake Constance suggesting that adaptive feeding (i.e., a predator changing its diet based on the current prey abundances) and predator-prey interaction were the main driving forces of the population dynamics in spring. However, there would have been little to be done analytically, had I chosen the path of analysing a high-dimensional ODE model (including a large number of unknown parameters) constructed for a "simple'' network of adaptively feeding ciliates and their different types of algal prey in Lake Constance. In addition, the existing literature on predator-prey models seemed so colossal that taking a different modeling framework from smooth ODEs sounded like a fresh direction that could be both biologically and mathematically interesting to pursue. As a result, I incorporated adaptive feeding into a model for one predator and two prey by using piecewise-smooth dynamical systems. In addition to its use for studying plankton, the system I developed turned out to be very rich mathematically: it exhibits a novel bifurcation, suggests a mechanistic explanation for the observed dynamics, and works as a motivating example of how traveling from one modeling framework to another can greatly increase both the mathematical and applicational understanding of an interdisciplinary research question.

Assuming that the predator behaves as an optimal forager that chooses its diet based on whichever prey choice maximizes its energy intake, I wrote down a piecewise-smooth dynamical system in which the predator switches between its two prey types (for an illustration, see Figure 1, left) [2]. In such a system, the phase space is divided into two (e.g., in this case, one part describes the Lotka-Volterra interaction between the predator and its preferred prey (\(f_+\)), while the other one describes that of the predator and its alternative prey (\(f_-\)) (see Figure 1, left)) or more smooth regions by one or more switching manifolds (\(h\)) that mark transitions between the regions:

(1)\begin{equation} \dot{{\mathbf x}}= \left\{ \begin{array}{rl} f_+({\mathbf x}), & \mbox{ if $h(\mathbf x)>0$} \\ f_-({\mathbf x}), & \mbox{ if $h(\mathbf x)<0$} \end{array} \right.\,. \end{equation}

Piecewise-smooth dynamics occur in a myriad of applications varying from mechanical oscillators to relay-feedback systems, and from gene regulatory networks to conceptual climate models. They can be used to approximate strongly nonlinear terms, such as sigmoidal or cubic functions, in models for systems that incorporate sharp transitions between two or more states. All of the dynamical behavior that can occur in smooth dynamical systems can also occur in piecewise-smooth systems as well, especially for bifurcations that occur far from a switching manifold. In addition, piecewise-smooth systems exhibit novel dynamics that do not occur in smooth systems. These scenarios include, for example, a situation when the switching boundary is attracting from both sides of the discontinuity and the system exhibits sliding (see \(f_s\) in Figure 1, middle and right) or when a vector field has a tangency with a switching boundary (see Figure 1, right), to mention only few.

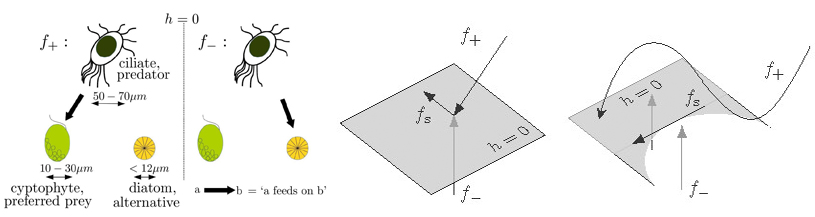
Figure 1: (Left) Model diagram for a three-dimensional piecewise-smooth system in which the ciliate predator population (which constitutes an important link between the bottom and higher levels of the aquatic food chain) feeds on either its preferred prey type (green) that does not invest energy in predator defense mechanisms or its alternative prey type (orange) that builds a hard silicate cover making the prey less susceptible to predation. (Middle and right) Possible dynamics in a piecewise-smooth system close to the switching manifold include sliding along the sliding vector field (\(f_s\)) and (right) one of the basic tangencies between a piecewise-smooth vector field and a switching manifold occurs at a cubic tangency.

In the case of the piecewise-smooth system for a ciliate predator and its two algal prey, the switching manifold is two-dimensional and tilted, and its slope corresponds to a prey preference trade-off (in which an increase in energy gained from one prey type comes at a cost of a decrease in the energy gained from the other prey) [2]. The slope of this ecological trade-off is not known, which made it an interesting parameter to adjust. Moreover, a steep or shallow slope can be related to a "picky'' (i.e., a selective interception-feeder) or an "accepting'' (i.e., an unselective filter-feeder) ciliate-predator, which is a result of the analytical and numerical explorations that could be experimentally tested. As a result of changing the slope, there is a transition from a center located entirely on the switching boundary to a periodic orbit that evolves partly along the boundary and partly outside of it. In addition, by increasing the distance to the bifurcation point, the periodic orbit experiences a period-doubling, which suggests a possible cascade to chaos. Together with my PhD advisers Mason A. Porter and Philip K. Maini, we named such a previously unknown bifurcation as as a center to two-part periodic orbit bifurcation (C2PO) bifurcation. The C2PO bifurcation satisfies all of the defining and non-degeneracy conditions of the adding-sliding bifurcation in piecewise-smooth systems. This suggests that a normal form for it could be computed by taking advantage of the existing calculations for the normal form of the adding-sliding bifurcation.

I implemented an existing algorithm of approximate Bayesian computation (i.e., a set of methods for approximate Bayesian inference that can be used whenever sampling from the model is possible) combined with Monte Carlo simulations to fit model parameters and compare model simulations to Lake Constance data. Indeed, the model successfully reproduces the periodic pattern early in the growing season when one can argue that predator-prey interactions govern the protist-algae dynamics more than physical driving forces in water masses that are rich in nutrients (see Figure 2, left). While the 1-predator 2-prey piecewise-smooth system provides prey switching as a possible mechanistic explanation for the observed patterns of plankton population oscillations [2], it is not clear whether such "discontinuous" predator feeding behavior exists. Therefore, the next steps were to develop smooth analogs of the piecewise-smooth system, compare their dynamical behavior, and use data to get more insight into the steepness of prey switching.

Figure 2: (Left) (Dashed curve) Scaled prey ratio for simulations of a 1 predator 2-prey system (for model equations, see [2]); (points) mean data calculated for the scaled prey ratio in spring in Lake Constance over the period 1979–1999; and (solid curve) processed data. The processed data is obtained by subtracting a least-squares fit of a straight line (dash-dotted lines) to the means of the data and the detrended data is then rescaled to have a minimum of 0. (Middle) The red asterisks give the normalized predator abundance for simulations of a 1-predator 2-prey model in the framework similar to the one given in Equation (2) (for model equations, see [1]). To guide the eye, the simulation is shown in red between the asterisks. Blue circles are data points for an unselective ciliate-predator in spring in Lake Constance in 1991 and blue lines between the points are for guiding the eye. (Right) Bar plot for the frequency of \(k\) values at the final iteration of our implementation of the PMC ABC algorithm originally developed by Beaumont et al. (Biometrika 96, 2009) for the same predator group as in the middle panel in spring in Lake Constance in 1991.

In general, one can derive different smooth approximations to the same piecewise-smooth system, e.g., by "smoothing out'' a discontinuity of a piecewise-smooth system using a differentiable transition function of sigmoidal form or by "regularizing'' a piecewise-smooth dynamical system into a singular perturbation problem that includes multiple time scales by "blowing up'' the switching boundary. In my thesis work, I considered two different ways of the former approach. First, a smooth analog for (1) can be obtained by using the smooth hyperbolic tangent function as follows:

(2)\begin{equation} \dot{{\mathbf x}} = \left(\frac{1+\text{tanh}(k(h(\mathbf x)))}{2}\right)f_{+}({\mathbf x})+\left(\frac{1-\text{tanh}(k(h(\mathbf x)))}{2}\right)f_{-}({\mathbf x})\,, \end{equation}

where \(k\) denotes the slope of the switching function. Second, incorporating a parameter that changes abruptly (between \(0\) and \(1\) in this case) across the switching boundary as a system variable that is coupled to the population dynamics results in the following four-dimensional smooth analog for (1):

(3)\begin{align} \dot{{\mathbf x}} &= {\mathbf g}(\mathbf x,q)\,,\nonumber\\ \dot{q} &= q(1-q)h(\mathbf x)\,. \end{align}

Parameter fitting of the three-dimensional smooth analog (2) to data showed not only that large \(k\) values fit the data better than small (see Figure 2, middle and right) but also that the best fit for the four-dimensional model (3) occurs in a parameter regime in which the fourth "switching'' variable \(q\) oscillates abruptly between its maximum and minimum values [1]. Motivated by these findings and by the fact that, biologically, the switching variable \(q\) can be considered as a predator trait that undergoes rapid evolutionary change in response to changes in the prey population dynamics, I then constructed a multiple time scale system in which one introduces and exploits a time-scale difference (given by \(\epsilon\), with \(0<\epsilon\ll1\)) between the demographic (\(\mathbf g\)) and predator trait (\(q\)) dynamics:

(4)\begin{align} \dot{{\mathbf x}} &= {\mathbf g}(\mathbf x,q)\,,\nonumber\\ \epsilon\dot{q} &= q(1-q)Vh(\mathbf x)\,. \end{align}

From a biological perspective, the system in (4) describes rapid predator evolution according to the fitness-gradient dynamics and \(q(1-q)V\) is the additive genetic variance. Using singular perturbation theory, it is possible to characterize different patterns of population oscillations (and compare them to those observed experimentally) exhibited by the 1 predator 2-prey system when the predator trait undergoes evolutionary change by concatenating solution trajectories that are determined by the fast or slow reduced dynamics when \(\epsilon=0\) and persist for \(\epsilon>0\) [3].

Although at the extremes (i.e., when \(k\to\infty\) (2) and when \(q=0/q=1\) (4)) a smooth analog may agree with its piecewise-smooth counterpart, the dynamical behavior of the two systems may not always be the same. For example, smoothing with a hyperbolic tangent function preserves the densities at, and stability of, the coexistence equilibrium, whereas smoothing that introduces an extra dimension to the system changes the stability of the same equilibrium. In addition, a smooth analog may also exhibit convergence to an equilibrium when there is a periodic orbit in the piecewise-smooth system. Therefore, data comparison plays a crucial role in getting biological insight into the steepness of a discontinuous switch or choosing between different competing models.

As a summary, I was very lucky to get access to data early on in my PhD. It was also crucial to get in touch with experimentalists and experts in the specific fields of dynamical systems, and having the two disciplines present at all times was something that I really enjoyed. There were several times when either the mathematical or the biological aspect of the project ground to a halt, while the other one kept me going -- let alone how much inspiration was transferred back and forth between the two disciplines. In my opinion, such a situation is doing science at its best.

References

[1] S. H. Piltz, L. Harhanen, M. A. Porter, and P. K. Maini, Two smooth analogs for a piecewise-smooth 1 predator-2 prey system, arXiv:1610.07094 [math.DS], 2016. In revision.

[2] S. H. Piltz, M. A. Porter, and P. K. Maini, Prey switching with a linear preference trade-off, SIAM Journal on Applied Dynamical Systems, 13 (2014), pp. 658-682.

[3] S. H. Piltz, F. Veerman, P. K. Maini, and M. A. Porter, A predator-2 prey fast-slow dynamical system for rapid predator evolution, SIAM Journal on Applied Dynamical Systems, 16 (2017), pp. 54-90.