Self-assembly of amphiphilic or dipolar molecules such as lipids, surfactants, and synthetic diblock copolymers finds wide application to energy production, [Garay et al (2014)], energy harvesting, [Choi et al (2010)] and biological cellular function [Friedman & Voeltz (2011)] and human disease, [Gluchowski et al (2017)]. The shorter members of the family of amphiphilic molecules include the phospholipid molecules that are the building block of choice of biological membranes and the surfactants that lower the free energy of mixtures by packing into the void spaces that form at the interfaces between incompatible fluids.
Figure 1. Hydrophobic/grey and hydrophilic/circled moieties of classical amphiphilic molecules.
Phase field models for the energy of multicomponent blends of amphiphilic molecules and solvents have been derived from the random phase approximation of self-consistent density functional theory. These models, including the well-known Ohta-Kawasaki free energy, incorporate entropic effects of chain folding through interactions with mean-field terms that yield linear differential effects that span four orders. Nonlinear terms are typically incorporated in an ad hoc manner based upon slowly varying averages and incompressibility. Gradient flows of these models support structures that include bilayers as well as cylindrical and spherical micellular forms. However they do not show evidence for the dynamic formation of defect states, such as end-caps and complex network structures, that play a substantial role in experiments of dispersions of amphiphilic diblock polymers. We present a variation of this random phase reduction that strengthens the role of nonlinearity and leads to the Multicomponent Functionalized (McF) free energy, which contains the Functionalized Cahn-Hilliard (FCH) free energy under a reduction to a scalar phase field function. The McF derivation differs from [Uneyama & Doi (2005a)] and [Choksi & Ren (2003)] in two key ways. The random phase approximation generically yields a bilinear approximation to the energy. [Uneyama & Doi (2005a)] use a slowly varying average phase approximation to extrapolate from the bilinear model, replacing the the average molecular density with the spatially varying density. In the McF derivation the average density is replaced with a long-range convolution of the density which better represents a slowly varying average. The second distinction represents a difference in scaling regime. [Choksi & Ren (2003)] obtain a singular limit by scaling the molecular chain length of the diblock molecule to infinity. Commensurate with a short molecule assumption, the McF scaling takes the ratio of the Kuhn length to domain size as a small parameter while keeping the chain length fixed. This results in a homogeneous scaling of the differential operators with this small parameter.
We present a family of benchmark problems for the scalar FCH that show that the formation of defect structures, corresponding to local minimizers, can arise from dynamic effects associated to the rate of absorption of dispersed molecules onto a bilayer interface. Slow rates of absorption lead to a regularized interfacial lengthening regime that can be described rigorously. Simulations, supported by linear bifurcation analysis, show that higher rates of absorption lead to formation of defects such as end-caps and loops observed experimentally. We present an energy for a blend of phospholipid and cholesterol, which contains an additional small parameter consistent with the McF derivation. The result is a singularly perturbed problem for the cholesterol-loaded structure embedded within the singular scaling of the phospholipid bilayer. Exploiting the semi-strong scaling of singular perturbation theory we show that the cholesterol sublayer robustly stabilizes the membrane to defect-generating pearling perturbations.
Multicomponent Functionalized (McF) free energies
[Choksi & Ren (2003)] and [Uneyama & Doi (2005a)] exploit random phase approximations of self-consistent mean field theory approaches to derive macroscopic models of free energy of di-block and homopolymer blends. Their approach recovers a bilinear form for the energy of mixtures of species \(\{\phi_i\}_{i=1}^n\) whose densities \(\phi_i=\overline{\phi}_i+\phi_{i,0}\) are small perturbations \(\phi_{i,0}=\phi_{i,0}(x)\) from the corresponding spatially averaged value \(\overline{\phi}_i|)\). On a fixed domain \(\Omega\), subject to periodic boundary conditions one may introduce the "Square-root Greens Operator" \({\mathrm G}:=(-\Delta)^{-\frac12}\), and write the energy as a bilinear form
| |
\(\begin{aligned}
\cal F^{(2)}_{\rm UD}(\phi_0) = &\sum_{ij}\int_\Omega \frac{A_{ij}}{\sqrt{\bar{\phi}_i\bar{\phi}_j}} ({\mathrm G} \phi_{i,0}) ({\mathrm G} \phi_{j,0}) +
\left(\frac{B_{ij}}{\sqrt{\bar{\phi}_i\bar{\phi}_j}}+ \chi_{ij}\right)\phi_{i,0}\phi_{j,0} \\ &\hspace{1.2in} + \delta_{ij} \frac{C_i}{\bar{\phi}_i} |\nabla \phi_{i,0}|^2\, dx.
\end{aligned}\) |
(1) |
Here \(A=(A_{ij})\), \(B=(B_{ij})\), \(C=(C_i)\) are material parameters that incorporate the diblock structure and scale with the diblock ratios, \(\chi_{ij}\) are related to Flory-Huggins interaction parameters, and \(\delta_{ij}\) is the usual Kronecker delta. [Uneyama & Doi (2005a)] extend this to a nonlinear model by viewing the average values as slowly varying, making the replacement
\(\boxed{\overline{\phi}_i\rightarrow \phi_i=\overline{\phi}_i+\phi_{i,0},}\)
and extrapolating the modified bilinear form into a fully nonlinear energy:
\(\begin{aligned}
\cal F_{\rm UD}(\phi) &= \sum_{ij}\int_\Omega\Bigl[ A_{ij}{\mathrm G} \sqrt{\phi_i} \, {\mathrm G} \sqrt{\phi_j}+ B_{ij}\left[(1-\delta_{ij})\sqrt{\phi_i\phi_j}+\delta_{ij} \phi_i\ln\phi_i\right]\\ &\hspace{1.2in} +\chi_{ij}\phi_{i}\phi_{j} + \delta_{ij} \frac{C_i}{\phi_i} |\nabla \phi_{i}|^2\Bigr]\, dx.
\end{aligned}\)
For the case of a single A-B type diblock copolymer both [Choksi & Ren (2003)] and [Uneyama & Doi (2005a)] use their extrapolated energy to re-derive the well-known Ohta-Kawasaki model. In [Uneyama & Doi (2005b)] this formulation was specified to model the energy of interaction of an amphiphilic diblock copolymer with a solvent, and was used to recover a smooth bifurcation sequence similar to the experimental results depicted in the bottom row of Figure 2 (left). This model was not able to recover the "morphological complexity" seen in the top row (left-longer chains) and depicted in the center images.
Phase field models of amphiphilic blends predate the random phase approximation, originating with [Teubner & Strey (1987)] who studied the small-angle x-ray scattering (SAXS) data of microemulsions of oil, water, and surfactant. They proposed a bilinear form for a scalar phase function that is comparable to the model \({\cal F}^{(2)}_{\rm UD}\). This model was extended in an ad-hoc manner to a nonlinear model similar to the FCH by [Gompper & Schick (1990)]. This form can be approached from the bilinear form (1). The first step is to rewrite the bilinear form in terms of the the local average \(\psi_i:={\mathrm G} \phi_{i,0}/\overline{\phi}_i\), and then extrapolate the bilinear energy \({\cal F}^{(2)}_{\rm UD}\) by replacing \(\overline{\phi}_i\) with the slowly varying average value
\(\boxed{ \overline{\phi}_i \rightarrow \overline{\phi}_i+ \overline{\phi}_i \psi_i.}\)
This extrapolation yields the general multicomponent functionalized (McF) free energy
\(\begin{aligned} {\cal F}_{\rm McF} := &\sum_{ij} \int_\Omega \frac{A_{ij}\overline{\phi}_{ij}\psi_i\psi_j }{\sqrt{(1+\psi_{i})(1+\psi_j)}} +
{{ \left(\frac{B_{ij}\overline{\phi}_{ij}}{\sqrt{(1+\psi_i)(1+\psi_j)}}+\overline{\phi}_{ij}^2\chi_{ij}\right)}} \nabla\psi_i \nabla \psi_j\\& \hspace{1.2in} +C_i\delta_{ij} \overline{\phi}_i |\Delta \psi_i|^2\,dx,\\ \end{aligned} \)
where we have introduced \(\overline{\phi}_{ij}:=\sqrt{\overline{\phi}_i\overline{\phi}_j}\). For simplicity the coefficient of the highest-order differential term is kept spatially constant. We rescale following \cite[Appendix A]{Choksi-03} [Choksi & Ren (2003)] with the exception that the chain length, \(N\), is kept finite as is commensurate with a short chain limit, rather than sent to \(\infty\) as in their derivation of Ohta-Kawasaki. As a consequence all differential terms scale homogeneously with \({\epsilon}\ll 1\), the ratio of the Kuhn length to the domain size. Modulo some compatibility conditions the McF energies can be written in the factored form
| |
\({\cal F}_{\rm McF}(\psi) := \int_\Omega \frac12 \left | {\epsilon}^2 D^2 \Delta \psi - F(\psi)\right|^2 - P(\psi),\) |
(2) |
where \(\psi=(\psi_1, \ldots, \psi_n)\), \(D\) is a positive diagonal matrix that reflects differences in molecular lengths, \(F:\mathbb{R}^n\mapsto\mathbb{R}^n\), and \(P:\mathbb{R}^n\mapsto\mathbb{R}\). We supplement this framework with incompressibility constraints \(\psi={\mathbb{I}}(u)\) where the map \({\mathbb{I}}:\mathbb{R}^d\mapsto\mathbb{R}^n\), indicates the relation between the packing of molecules and the intrinsic pressure.
Reduction to Functionalized Cahn-Hilliard
The simplest amphiphilic blend consists of an A-B diblock mixed with a solvent \(C\). We consider the McF with \(\psi=(\psi_A, \psi_B, \psi_C)\). To reduce to a scalar model, we impose a two-constraint incompressibility
\(\boxed{\psi_A=f_A u, \hspace{0.2in}\psi_B=f_B u, \hspace{0.2in} \psi_C=1-u,}\)
where \(f_A+f_B=1\) are the molecular weight fractions of the \(A\) and \(B\) monomers within the chain. Inserting this reduction into the McF, our analytical results require that \(P\) is small, so that the energy is close to a "perfect square". This yields the functionalized Cahn-Hilliard energy
\( {\cal F}_{\rm FCH}(u) := \int_\Omega \frac12\left( {\epsilon}^2\Delta u -W'(u)\right)^2 - {\epsilon}^p P(u)\, dx,\)
where \(W:\mathbb{R}\mapsto \mathbb{R}\) is an unequal depth double-well potential whose second derivative $W''$ tends to \(\infty\) as \(u\to 0,1\) and \(p=1,2\) characterizes the strength of the functionalization terms that break the perfect square structure. Within the synthetic polymer community, "It has been established that the nanoparticle morphology is a result of a reduction in free energy achieved via three main parameters: (i) stretching of the hydrophobic core block, (ii) interfacial tension between the core and solvent, and (iii) repulsion between corona strands. Each of these components involves contributions from myriad variables in the polymer structure and environment", [Barnhill et al (2015)]. These effects can be incorporated via the reduction
\( P(u) = \frac12 \eta_1 {\epsilon}^2 |\nabla u|^2 + \eta_2 W(u),\)
with the parameter \(\eta_1\) describing effects (ii) and \(\eta_2\) incorporating the aspect ratio of the surfactant molecules which underlies effects (i) and (iii). To this list [Barnhill et al (2015)] add a kinetic parameter, the "unimer exchange rate" governing the rate of insertion or expulsion of amphiphilic molecules between a micellular structure and the bulk phase. Within the FCH this is governed by the value of the second derivative of the double well at the pure solvent phase, \(W''(0)\) -- that controls the energy of dilute dispersions of surfactant and determines the energetic reward for insertion of an amphiphilic molecule into a micellular structure.
Curve Lengthening and Defects in FCH Gradient Flows
Addressing the FCH energy, at leading order the codimensional structures are solutions of the global minimization problem associated
to the dominant form
| |
\({\epsilon}^2 \Delta u - W'(u)= O({\epsilon}),\) |
(3) |
while defects solve the local minimum problem
| |
\(({\epsilon}^2 \Delta -W''(u))({\epsilon}^2\Delta u -W'(u)) ={\epsilon} \lambda,\) |
(4) |
in terms of a Lagrange multiplier \(\lambda\in\mathbb{R}\). Experimental results, [Jain & Bates, 2003], examine the relaxation of a dispersion of amphiphilic PEO-PB diblocks in solvent. Forming dispersions with hydrophobic chain length \(N_{\rm PB}=45\) and \(N_{\rm PB}=170\), they found that the short hydrophobic chain molecules self-assembled into `defect free' states with various dominant co-dimensions depending upon the weight fraction \(w_{\rm PEO}\) of the hydrophilic to the hydrophobic monomers within the diblock chain. However for the longer hydrophobic chains they observed that bilayer structures were replaced defect heavy structures, whose appearance they described as the onset of "morphological complexity." For analytical and computational purposes we study gradient flows of the FCH energy associated to a family of benchmark problems arising from initial data that replaces the random dispersion of amphiphilic material with a fixed, slightly non-circular bilayer interface perturbed by a small, spatially constant density of dispersed molecules. These benchmark problems illuminate the rich interplay between codimensional structures and defects, in particular they show that the onset of morphological complexity can be attributed to the rate of absorption of surfactant materials from the bulk dispersion. Analysis of linearization of the FCH energy at a bilayers structure shows two natural soft modes: one associated to interfacial motion, called meander modes, and one associated to high-frequency perturbations of the interfacial width, called pearling instabilities, [Kraitzman & Promislow (2018)]. Both instabilities are very sensitive to the level of dispersed surfactant. Simulations of the FCH gradient flow
| |
\(u_t = \Delta\frac{\delta {\cal F}_{\rm FCH}}{\delta u} = \Delta\left(({\epsilon}^2\Delta - W''(u))({\epsilon}^2 \Delta u -W'(u)) + {\epsilon}^p(\eta_1 {\epsilon}^2 \Delta u-\eta_2 W'(u))\right),\) |
(5) |
starting from the benchmark initial data show that low levels of dispersed surfactant lead to a buckling motion as the bilayer lengthens to absorb the dispersed surfactant. Increasing the level of dispersed surfactant leads to a pearling bifurcation which then yields to a bike-chain motion of the resulting micelles. The embedded pearls may protrude and produce end-caps that subsequently enlarge and may re-intersect with the bilayer to form loops. Initial data with yet higher levels of dispersed surfactant can lead directly to curve splitting and loop formation. These three outcomes are presented in Figure 2 (right).
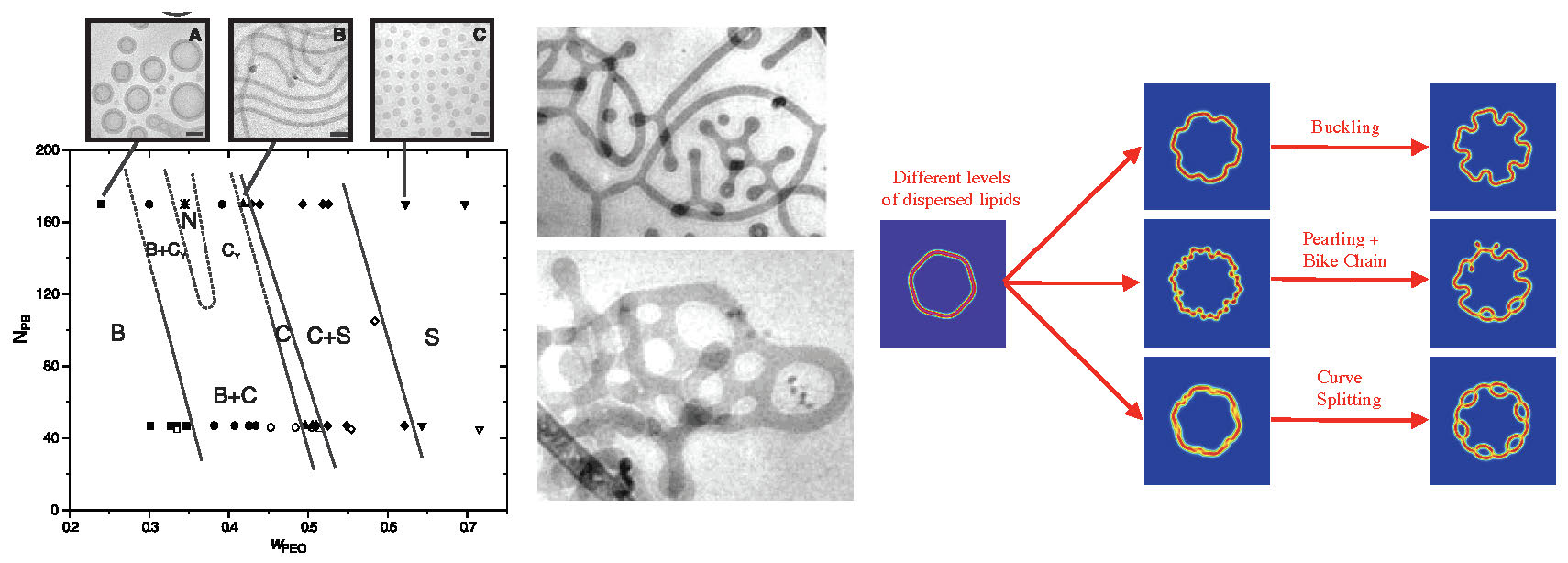
Figure 2. (left) Experimental morphology of Polyethylene oxide (PEO) - Polybutadiene (PB) amphiphilic diblock as function of the PEO weight fraction, \(w_{\rm PEO}\), (horizontal axis) for molecular weights of PB fixed at \(N_{\rm PB}=45\) and \(170\) (vertical axis). Morphological Complexity is observed for \(N_{\rm PB}=170\) but not for the shorter \(N_{\rm PB}=45\) chains. (center) Experimental images from the morphological complexity regime showing network structures, end caps, and \(Y\)-junction morphologies corresponding to the \(C_Y\) phase of the bifurcation diagram, [Jain & Bates, 2003]. (right) FCH benchmark simulations from perturbed bilayer plus dispersion of surfactant which are absorbed under gradient flow. Increasing dispersion level leads to (top to bottom) buckling, pearling and bike-chain evolution that generates endcaps and loops, and curve splitting that generates loops.
For the benchmark problems, rigorous analysis of [Chen & Promislow (arXiv)] applied to the strong functionalization, \(p=1\) in (5), establishes a finite dimensional reduction for the the curve lengthening evolution for sufficiently low levels of dispersed surfactant. Using a large-dimensional center-stable manifold reduction, it is shown that the evolution of a bilayer interface \(\Gamma\) immersed in \(\Omega\subset\mathbb{R}^2\), is well approximated by the gradient flow of the sharp interface energy
\( {\cal F}_\Gamma:= \frac{\alpha}{2} {\epsilon}^{-1}\bigl ||\Gamma|-\gamma_0\bigr|^2 + \frac{\nu}{2} \int_\Gamma \kappa^2\, ds,\)
where \(\alpha,\nu>0\) are constants, \(\kappa\) is the curvature of \(\Gamma\), \(|\Gamma|(t)\) is the length of the evolving bilayer interface and \(\gamma_0\) is an equilibrium curve length specified from the initial data via mass conservation. If the initial curve length is shorter than the equilibrium value, \(|\Gamma_0|<\gamma_0\), the curve lengthen increases through motion against curvature subject to regularization by Willmore terms. In two space dimensions this flow can be characterized in a more familiar PDE setting in terms of its impact on the curvature,
\(\partial_t \kappa = {\epsilon}^{-1}\left(\partial_s^2 + \kappa^2\right)\left(\alpha(|\Gamma|-\gamma_0) \kappa + {\epsilon}\nu \left( \partial_s^2 \kappa + \frac12 \kappa^3\right) \right).\)
The regularizing Willmore terms represent a singular perturbation that allows for well-posedness of the flow. Rigorous [Kraitzman & Promislow (2018)] and formal analysis, [Christlieb et al (2019)], characterizes the onset of pearling via a pearling stability index that incorporates the level of dispersed surfactant. This was followed by work using spatial dynamics techniques to establish the existence of stable pearled structures, see [Promislow & Wu (2015)] and [Promislow & Wu (2017)]. However the pearled morphology can be transient as it is sensitive to the evolving level of dispersed surfactant. This situation is presented in the following movie that presents a simulation of the FCH gradient flow for a dispersed surfactant level that is just below the critical level required to generate a defect.
The two graphs on the right-hand side present the evolution of the pearling stability index and the value of the coefficient \(\alpha(|\Gamma|-\gamma_0)\) whose sign drives the transition from curve lengthening to curve shortening. The movie shows a rapid transition of the bilayer to a pearled morphology accompanied by a sharp decrease in the pearling stability index. However the onset of the pearled morphology inhibits the absorption of dispersed surfactant and the pearling-stability index is held near the pearling-neutral line from \(t=5\) to \(t=20\). During this time the pearls undergo a bicycle chain motion in which adjacent pearls are dislocated in alternate directions -- a sort of pearled meander. This motion only slightly increases the amount of surfactant absorbed onto the pearled bilayer. At \(t\approx 20\) two new pearls are generated, allowing the curve to lengthen, lowering the pearling index into a stable value, and the pearled bilayer relaxes back to an un-pearled bilayer form. The last micelle-type defect is, narrowly, reabsorbed around \(t=35\), at roughly the end of the curve-lengthening regime. Subsequent motion, not shown, restores the interface to a larger circular shape.
The simulations suggest that it is the rate of absorption of the dispersed surfactant that is deterministic in the formation of defects. This is partially justified by the analytical results. Indeed, the bilayer buckling analysis show that a nearly-circular initial bilayer has a departure from circularity that depends exponentially upon the initial level of dispersed surfactant -- beyond a key threshold the growing curve will surely self-intersect. Similarly the pearling stability index depends sensitively upon both the background level of surfactant and the value of \(W''(0)\) that controls the rate of absorption. These analytical results are consistent within the experimental results presented in Figure 2 (left). The longer chained molecules are considerably more hydrophobic and encumber more volume per molecule [Jain & Bates (2004)]. This corresponds to both a higher absorption rate and a higher displaced volume per molecule. Preliminary simulations of the FCH gradient flow show that increasing \(W''(0)\) for initial data with the same initial level of dispersed surfactant triggers a chain of bifurcations similar to morphological complexity.
Singular Perturbations and Phospholipid-Cholesterol Models
Figure 3. Interdigitation of cholesterol molecule between two phospholipid molecules.
The pearling resultant morphological complexity observed in synthetic polymers is not observed in the phospholipid bilayers that comprise in vivo cell membranes. A potential mechanism for the robust stability of the biological membranes can be gleaned from the observation that all eukaryotic cells interdigitate cholesterol in a roughly 1-1 ratio with phospholipid molecules (non-eukarotic cells often contain simpler glycolipids). Considering a model for a phospholipid-cholesterol-solvent blend with variables \(\psi:= (\psi_H,\psi_T,\psi_C, \psi_S)\) denoting head and tail groups of the phospholipid, the cholesterol molecule approximated by a chain of a single monomer, and solvent phase, we impose an incompressibility constraint that slaves \(\psi={\mathbb{I}}(u_1,u_2)\) with \(u_1\) denoting a unified phospholipid head-tail and \(u_2\) the cholesterol density. This model exactly satisfies the compatibility constraints required for reduction to the factored form (2). Assuming an asymptotically small functionalization term \(P\), the bilayer structures correspond to homoclinic solutions of the reduced ODE:
| |
\(D^2\partial_z^2 \begin{pmatrix} u_1\cr u_2 \end{pmatrix} = \begin{pmatrix} F_1(u_1,u_2)\cr F_2(u_1,u_2)\end{pmatrix}.\) |
(6) |
Additional assumptions on Florey-Huggins parameters corresponding to strongly amphiphilic phospholipid and weakly hydrophilic cholesterol molecules, and a dominant volume fraction of solvent yields a system with a singularly perturbed scaling within the matrix \(D=\)diag\(\{1,\delta\}\). Indeed the nonlinearity \(F\) is of the form for which \(F_1(u_1,0)\) and \(F_2(0,u_2)\) both support bilayer profiles in \(u_1\) and \(u_2\) and satisfy \(\partial_{u_2}F_1 \gg \partial_{u_1}F_2\). These features fit hand-in-glove with the semi-strong scaling of singularly perturbed dynamical systems studied in [Doelman & Veerman (2013)] and [Doelman & Veerman (2015)].
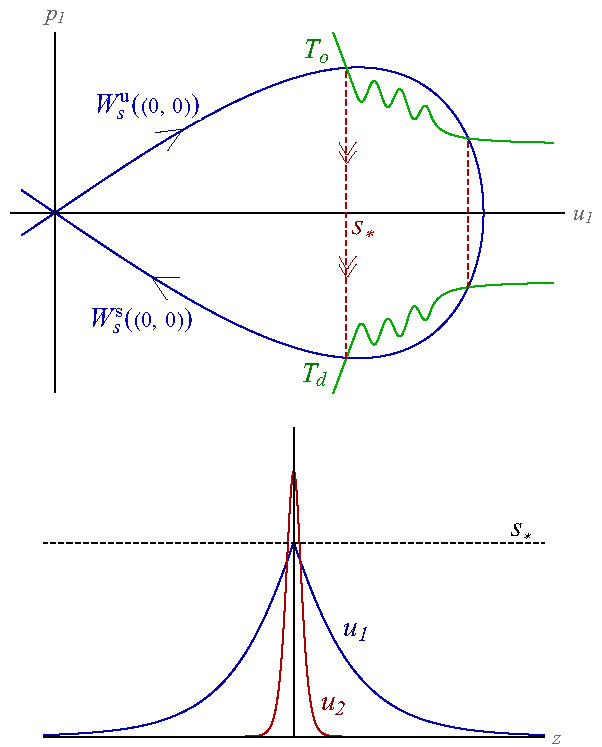
Figure 4. (top) The phospholipid cholesterol bilayer system (6) with \(F\) given in (7) has two fast-slow homoclinic connections, corresponding to the two intersections of the take-off curve \(T_o\) with the unstable manifold \(W_s^u\) of the origin of the slow system \((u_1)_{zz} = W'(u_1)\). The leftmost intersection, at \(u_1=S_*\), where \(T_o\) crosses the unstable manifold from above yields a robustly stable bilayer interface. (bottom) A cross section of a bilayer membrane with phospholipid (\(u_1\)) on the outside and interdigitated cholesterol (\(u_2\)) in the core where the maximum density is acheived. The maximum value of \(u_1\) occurs at the take-off intersection point. The amplitude of the fast component, \(u_2\), equals \(1/f(S_*)\), which is an adjustable parameter.
The linear nature of the random phase reduction of the self-consistent mean field theory only provides guidelines for the extrapolation to a more nonlinear model. The semi-strong singular perturbation toolbox allows one to identify a model that fits within this framework and has the desired composition and stability properties. Remarkably, these McF guidelines are consistent with a semi-strong singularly perturbed structure with a vector field of the form
| |
\(F(u) = \begin{pmatrix} W'(u_1) - \frac{1}{3\delta} f(u_1)^2 u_2^2 T_o(u_1)\\ u_2-f(u_1) u_2^2
\end{pmatrix},\) |
(7) |
and the diagonal matrix \(D=\)diag\(\{1, \delta\}\) with \(\delta\ll1\) denotes the length ratio of the cholesterol to the phospholipid molecule. Here \(f\) is a generic positive function satisfying \(f(0)=0\) that scales the density of cholesterol within the bilayer. A more central role is played by the take-off curve \(T_o\), and its intersection with the unstable manifold of the vector field at the origin. This affords both the construction of the bilayer profile \(\Phi\) that is a homoclinic solution of the coupled system (6) and a sharp quantification of the eigenvalue structure of the associated linearization
\( {\cal L}:= D^2\partial_z^2 - \nabla_u F(\Phi).\)
This information was extended to the multidimensional problem for a bilayer embedded in \(\mathbb{R}^m\) and extrapolated to information on the McF linearization \({\mathbb{L}}:={\cal L}^\mbox{†}{\cal L}\) whose eigenvalues are precisely the singular values of \({\cal L},\) [Chen et al (arXiv)]. Indeed, a sharp pearling stability condition, requiring only that the scaled operator \(D^{-2}{\cal L}\) has no strictly positive real spectrum, can be linked to a very natural geometric condition associated to the crossing direction of the take-off curve and unstable manifold of the origin. It is impressive that the semi-strong technology can provide stability information in this higher-order/multi-dimensional setting. It is true synergy that the semi-strong technology can transform the expectations of robust stability of a phospholipid-cholesterol bilayer into an in-painting of the nonlinear structure that is missing from the random phase reduction while remaining within the guidelines it provides for scaling and compatibility. This highlights the role that analysis can play in model development.
References
[Barnhill et al (2015)] S. Barnhill, N. Bell, J. Patterson, D. Olds, and N. Gianneschi,
Phase diagrams of polynorbornene amphiphillic block copolymers in solution, Macromolecules, 48 (2015), pp. 1152-1161.
[Garay et al (2014)] L.Garay, K. Boundary-Mills, and J. German,
Accumulation of High-value lipids in single-cell microorganisms: A mechanistic approach and future perspectives, J. of Agricultural and Food Chemistry, 62 (2014), pp. 2709-2727.
[Choksi & Ren (2003)] R. Choksi and S. Ren,
On the derivation of a density functional theory for microphase separation of diblock copolymers, Journal of Statistical Physics, 113 (2003), pp. 151-176.
[Chen et al (arXiv)] Y. Chen, A. Doelman, K. Promislow, F. Veerman,
Robust Stability of Multicomponent Membranes: the Role of Glycolipids, submitted; https://biorxiv.org/cgi/content/short/2019.12.19.882092v1.
[Chen & Promislow (arXiv)] Y. Chen and K. Promislow,
Regularized curve lengthening in the strong FCH gradient flow, submitted, https://arxiv.org/abs/1907.02196.
[Christlieb et al (2019)] A. Christlieb, N. Kraitzman, K. Promislow,
Competition and Complexity in Amphiphilic Polymer Morphology, Physica D, 400 (2019), 132144.
[Choi et al (2010)] S.-H. Choi, T. Lodge, and F. Bates,
Mechanism of molecular exchange in diblock copolymer micelles: hypersensitivity to core chain length, Phys. Rev. Let., 104 (2010), 047802.
[Doelman & Veerman (2015)] A. Doelman and F. Veerman,
An explicit theory for pulses in two component, singularly perturbed, reaction diffusion equations, J. Dyn. and Diff. Eqns., 27 (2015), pp. 555-595.
[Doelman & Veerman (2013)] A. Doelman and F. Veerman,
Pulses in Gierer-Meinhardt equation with a slow nonlinearlity, SIAM Applied Dynamical Systems, 12 (2013), pp. 28-60.
[Friedman & Voeltz (2011)] J. Friedman and G. Voeltz,
The ER in 3D: a multifunctional dynamic membrane network,
Trends in Cell Biology, 21 (2011), pp. 709-717.
[Gompper & Schick (1990)] G. Gompper and M. Schick,
Correlation between structural and interfacial properties of amphillic systems, Phys. Rev. Lett., 65 (1990), pp. 1116-1119.
[Gluchowski et al (2017)] N. Gluchowski, M. Becuwe, T. Walther, R. Farese,
Lipid droplets and liver disease: from basic biology to clinical implications, Natature Reviews Gastroenterol Hepatol., 14 (2017), pp. 343-355.
[Jain & Bates, 2003] S. Jain and F. S. Bates,
On the origins of morphological complexity in block copolymer surfactants, Science, 300 (2003), (5618), pp. 460-464.
[Jain & Bates (2004)] S. Jain and F. Bates,
Consequences of nonergodicity in aqueous binary peo-pb micellar dispersions, Macromolecules, 37 (2004), pp. 1511-1523.
[Kraitzman & Promislow (2018)] N. Kraitzman and K. Promislow,
Pearling Bifurcations in the strong Functionalionalized Cahn-Hilliard Free Energy, SIAM Math Analysis 50, 3 (2018), pp. 3395-3426, DOI:10.1137/16M1108406.
[Promislow & Wu (2015)] K. Promislow and Q. Wu,
Existence of pearled patterns in the planar Functionalized Cahn-Hilliard equation, J. Differential Equations, 259 (2015), pp. 3298-3343.
[Promislow & Wu (2017)] K. Promislow and Q. Wu,
Existence, bifurcation, and geometric evolution of quasi-bilayers in the multicomponent functionalized Cahn-Hilliard equation, Journal of Mathematical Biology, 75 (2017), pp. 443-489.
[Teubner & Strey (1987)] M. Teubner and R. Strey,
Origin of scattering peaks in microemulsions, J. Chem. Phys., 87 (1987), pp. 3195-3200.
[Uneyama & Doi (2005a)] T. Uneyama and M. Doi,
Density Functional Theory for Block Copolymer Melts and Blends, Macromolecules, 38, pp. 196-205.
[Uneyama & Doi (2005b)] T. Uneyama and M. Doi,
Calculation of the Micellar Structure of Polymer Surfactant on the Basis of Density Functional Theory, Macromolecules, 38, pp. 5817-5825.