1 Introduction
Rioting and civil disobedience have been and continue to be a popular means for a community to convey their dissatisfaction with their current living situations [30]. This can be a result of many factors, including political suppression [27], food scarcity [39], high unemployment [17], police brutality [3, 26], or racial tension [27] among many others. In present times, we see the development of these bursts of social activity throughout the world and at many scales. It is then of interest to understand the scale of the activity and the factors that determine whether bursts of activity will remain locally contained (and ultimately fizzle out) or persist and spread to surrounding regions. For example, the Arab Spring that was initiated in Tunisia in 2010 has spread throughout many regions in Africa and the Middle East and remained a strong movement until 2014 [25]. At smaller scales, we have recently observed the bursts of civil disobedience in Ferguson, Missouri that was triggered by the shooting of Michael Brown in 2014 followed by those in New York after prosecutors and a grand jury refused to indict a police officer in the death of Eric Garner [19]. These are just a few examples of this ubiquitous activity that occur in every corner of the world.
One can think of riots as bursts of activity that occur when the system is "ripe" (the stress or tension in the system is sufficiently high) and that are initiated by a "triggering event," an external factor sparking an internal self-reinforcement of the system, where riots lead to more riots. These internal factors, also known as endogenous factors, keep the burst of activity going and growing for a period of time, after which the system experiences a sort of self-relaxation. The self-excitement in the system implies that the occurrence of one event will increase the probability that subsequent events occur. Models for systems which are believed to experience self-excitement, such as earthquakes, the number of views of YouTube videos, and residential burglaries, have been previously proposed [12, 29, 31]. The number of events that occur in these applications have been typically modeled by a Hawkes process (a Poisson process with an intensity that depends on previous events). Hawke's processes and similar models have also been proposed to describe the level of rioting activity - see for example [9, 10, 13, 20, 25] and references within. We take a different approach inspired by the recent use of PDE models to gain insight into a variety of social behavior, see for example [35].
A factor which is widely recognized as influencing the spread of riots and revolutions [1, 18] is that of increased access to social media and this has been partially included in some of the modeling - see [10, 13, 25]. For example, it is believed that during the 2011 London riots (dubbed as the "Blackberry riots") smart phones were used heavily to organize [15]. Also, preliminary data analysis for these riots has shown the importance of diffusion and clustering, calling for deeper investigations of this phenomena [3]. However, the effect of globalization of information has not been studied extensively mathematically. Indeed, most of the work modeling rioting activity has been focused on the temporal dynamics and not on the spatial spread, an important aspect to understand. This is clearly seen in the 2005 French riots where the deaths of two Paris teenagers sparked weeks of rioting in the Paris suburbs and in various cities throughout the country. The severity and duration of the rioting was such that France eventually declared itself to be in a state of emergency. It was the clear contagion of rioting activity of these particular riots which brought into focus the importance of understanding spatio-temporal dynamics of rioting activity. Motivated by this, Berestycki, Nadal, and Rodríguez introduced and analyzed some systems of partial differential equations in [4] that serve as basic models for the spread of rioting activity. These models include the effects of exogenous and endogenous factors as well as various mechanisms for dispersal of information. It is the objective of the present work to summarize the model introduced in [4] and provide a general survey of the analysis done in [4, 5, 6, 40].
2 The Model
We first present a single-site model, which is appropriate for understanding the temporal dynamics for aggregated data. Next, we mention the simplest (and most studied) model incorporating spatial contagion.
2.1 Single-Site Model
The quantities we are concerned about modeling are the level of rioting activity and a measure of the effective social tension in a system. Let us denote the these quantities by \(u\) and \(v\) respectively. For now, we only consider \(u\) and \(v\) as functions of time and satisfy the system:
| |
\(u_t(t)= r (v(t)) G(u(t)) - \omega u(t),\) |
(1a) |
| |
\(v_t(t)= - h(u(t)) v(t)+S(t)+1,\) |
(1b) |
for \(t>0\) and with non-negative initial data.
The function \(G\) is of KPP-type ([16]) and models self-excitement in the system. Specifically, we assume that \(G\) is of class \(C^3\) and satisfies
\(G''<0,\qquad G(0)=0,\qquad G(z)<0\quad\)for \(z\) large enough.
The prototypical \(G\) leads to logistic growth. However, self-excitement in the system is negligible until the tension \(v\) reaches a sufficiently large value; this switch mechanism is described by the function \(r\) which is a sigmoid function:
| |
\(r(z)= \frac{1}{1 + e^{-\beta(z-a)}}.\) |
(2) |
The parameter \(\beta>0\) provides a measure of the transition slope between the relaxed state (non-excited) and the excited state. In other words, it provides a measure of how fast the transition is between a system that does not include the self-excitement and a system with the full-force of these factors. The critical tension, here denoted by \(a\ge 0\), provides a measure of how large the tension needs to be before the switch (from relaxed to excited) is made. Note that in the limit \(\beta\to\infty\), \(r\) approaches the step function \(1_{[a,\infty)}\), in which case the self-excitement factors are in full-force as soon as the tension is above the critical threshold \(a\). We further assume that external events increase the tension \(v\) and are modeled by a Dirac delta. If \(n\) external relevant events occurs at times \(\{t_1,t_2,\dots,t_n\}\) with intensities \(A_i\) for \(i\in\{1,2,\dots, n\}\) then the source term has the form:
| |
\(S(t)=\sum_{j=1}^nA_j\delta(t-t_j),\) |
(3) |
where \(\delta\) is the Dirac mass centered at zero. The effect that the level of activity \(u\) has on the tension \(v\) is modeled by the term \(h(u)\), where
\(h:[0,\infty)\to(0,\infty)\quad\) is of class \(C^1,\)
and it is either monotone increasing or decreasing. Note that the monotonicity of \(h\) determines whether (1) is of cooperative or activator-inhibitor type. For this reason we refer to (1) in the case when \(h\) is decreasing as a tension-enhancing system and in the case when \(h\) is increasing as a tension-inhibitive system. The case when \(h\) is constant decouples the system. Considering the two cases allows us to differentiate between two different types of outbursts of activity from the modeling perspective. A typical example to have in mind is
| |
\(h(u)=\frac{\theta}{(1+u)^p}, \quad \theta>0,\) |
(4) |
which is tension enhancing if \(p>0\) and tension inhibiting if \(p<0\). Finally, from (1b) we see that \(+1\) is the normalized base social tension.
2.2 Multiple-Site Model
Considering the nearest neighbors contagion of the level of rioting activity and the social tension produces
the continuum model:
| |
\(\cases{u_t = d_1u_{xx}+r(v)G(u) - u, \quad x\in\mathbb{R}, \,\, t>0, \cr v_t = d_2v_{xx}-h(u)v+1+S(t).}\) |
(5) |
Naturally, \(u\) and \(v\) are now functions of \((x,t)\) and \(d_1\) and \(d_2\) are the diffusivity
coefficients of the level of rioting activity and the social tension, respectively.
Other contagion mechanisms can be considered, such as social media, which would lead to a
non-local spread of both quantities. This topic was briefly mentioned and studied in
[4], but there is still a great need for finding suitable ways to model these spreading
mechanisms.
3 Summary of Results
3.1 Homogeneous steady-state solutions
It is useful to have a clear understanding of the homogeneous steady-state solutions of system (5).
In [40] parameter regimes that yield different numbers of steady states for the spatially homogeneous system were found.
In that work, it was chosen to set \(a=1\) (all regimes of interest were observed in this case) and an analysis of the steady states was based on \(\beta, \Gamma\) and
\(p\). Due to the vast parameter space this analysis was partially analytical and partially numerical with the help of AUTO.
It is natural to consider the cases \(p>0\) and \(p\le 0\) separately. In the former case, if the steady states are restricted to physically relevant (non-negative) quantities, there is the possibility of two, three, or four steady states.
In the two steady state case, the system is monostable with one stable constant steady state.
In the three and four steady state case, the system is bistable with two stable constant steady states. For more details on the parameters which yield these different cases see [40]. In the latter case, again
the system is monostable with one stable constant steady state as long as \(\Gamma>2\). It is important to note that the bifurcation was done for small and fixed \(p\) (both positive and negative)
and it would be of interest to determine if indeed the maximum number of physical relevant steady-states is four by bifurcating in \(p\).
3.2 Single-Site Model with Periodic Source Term
An important aspect that was studied in [6] was the question of how
various continuous external events (referred to as "shocks") actually influence
the qualitative behavior of the level of rioting activity. There are many issues such as political decisions, the
state of the economy, global issues, to name a few examples, that
are continuously affecting the tension in the system. These effects are random and extremely difficult to quantify
exactly. Nevertheless, understanding the role that these types
of events, which are occurring on a regular basis, play in the temporal dynamics of the level of
activity is important.
The work in [6] focused on understanding
the effect that external events occurring on a periodic basis and with the same intensity have on the solutions to the
single site model. Specifically, it focused on the study of what happens when external events occur with a period \(T\)
and intensity \(A\).
Numerical simulations performed in [4] illustrate the existence
of periodic cycles for fixed intensity \(A\) and sufficiently high frequency in the case when \(h\) is decreasing.
More precisely, for a fixed intensity,
it was observed that if the period is above a threshold then the level of
activity is "over-damped" - in the sense that the solutions exhibit
oscillations which
quickly decay with time. On the other hand, for a sufficiently small period the
solutions converge to a periodic cycle. These findings were rigorously analyzed in
[6] both in the tension enhancing and tension
inhibitive cases. From the mathematical point of view,
the system behaves monotonically with respect to the intensity \(A\), whereas
in general there is no monotonicity in \(T\). For this reason that work investigates
how the dynamics changes when \(A\) varies. One can see that the
results can be used to describe the dependence on the
length of the period \(T\), recovering the numerical observations of
[4].
The system analyzed in [6] reads as follows:
\(\cases{u_t(t)= r (v(t)) G(u(t)) - \omega u(t),\cr
v_t(t)= - h(u(t)) v(t)+A\sum_{j=1}^\infty\delta(t-Tj),\cr
u(0)= U, \;v(0)=V.}\)
Additionally,
one must assume that
\(r(0)G'(0)<\omega<g'(0).\)
The interest of [6] was the study of cycles and on the long-term dynamics of the system.
A cycle is a solution \((u,v)\) to (1) that is periodic
with period \(T\). We say that the cycle is quiet if \(u\equiv0\),
otherwise it is excited.
Naturally, an excited cycle satisfies \(u(t)>0\) for all \(t\geq0\).
We will see in the next section that the quiet cycle always exists and that it
is stable if and only if the amplitude \(A\) of the source term is sufficiently small. In fact, the overall dynamics of the system drastically depends
on the value of \(A\).
The results in the tension-enhancing case, i.e. when \(h\) is decreasing, are
summarized in the following.
Theorem 3.1 (the tension enhancing case [6]).
Suppose that \(h\) is decreasing (in the large sense).
There exist then some thresholds \(0 < A^* ≤ A_0\) such that
- if \(A < A^*\) then all solutions converge to the quiet cycle (as \(t\to\infty\));
- if \(A^* < A < A_0\) then, for any \(U>0\), there exists \(V ≥ 0\) such that solutions with \(u(0)=U\) converge to the quiet cycle if \(v(0) < V\) and to an excited cycle if \(v(0) ≥ V\);
- if \(A > A_0\) then any solution with \(u(0)>0\) converges to an excited cycle.
The results in the tension inhibitive case, i.e. when \(h\) is increasing, are summarized in the following.
Theorem 3.2 (the tension inhibitive case [6]). Suppose that \(h\) is increasing. There exists then a thresholds \(A_0 > 0\) such
that
- if \(A < A_0\) then all solutions converge to the quiet cycle
- if \(A > A_0\) then any solution with \(u(0) > 0\) satisfies \(\inf_{t ≥ 0} u(t) > 0\), and moreover the system admits an excited cycle.
The key take away from these results is that for external events, which increase the tension of the system, occurring at a fixed rate
we expect a non-trivial amount of activity in the long-term if the intensity is sufficiently large. On the other hand, even if we have
an infinite number of events the rioting activity will converge to zero in the longer term if the intensity is sufficiently small.
3.3 Traveling Wave Solutions
A 2005 French dataset [14] provides the number of ``riot-like'' events (for example, burning cars, attacks upon police) for a 47-day period after October 27
in each of the country's departments. The dataset was obtained from the source data studied in
Cazelles et al [11] (see also [8], section Materials and Methods, for more details).
This dataset shows a peak of intense rioting behavior that spreads across France. We can see in Figure 1 that the rioting behavior reaches its maximum around day eight after October 27 in Department 93 where the neighborhood of the boys, Clichy-sous-Bois, is located.
Another example of the rioting data for Department 59 (the northermost department of France) is shown in Figure 2.
Here we see the qualitative behavior of the graph is very similar to that of Department 93. However, the peak in rioting behavior is reached around the
12th day after October 27, 2005, which implies that it takes some time for this intense rioting behavior to travel across France.
The right inset of Figure 2 shows the relative distance between Departments 93 and 59.
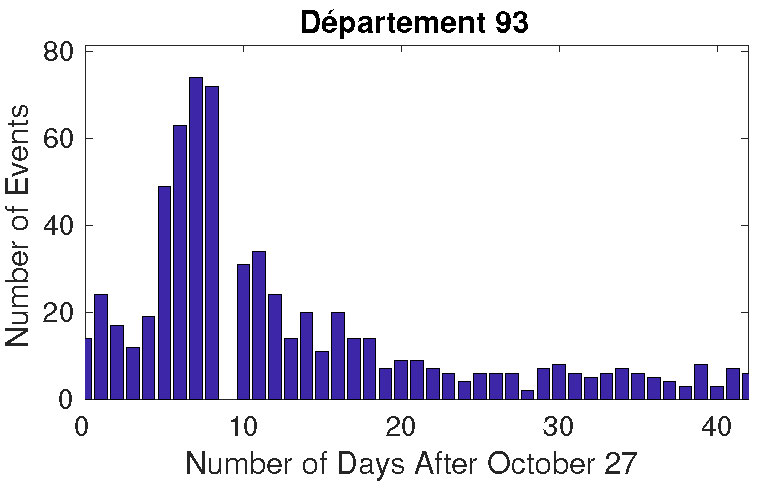
Figure 1. Left: the number of riot-like events on each day after October 27, 2005 in Department 93 of France. Right: the location of Department 93 in relation to Paris.
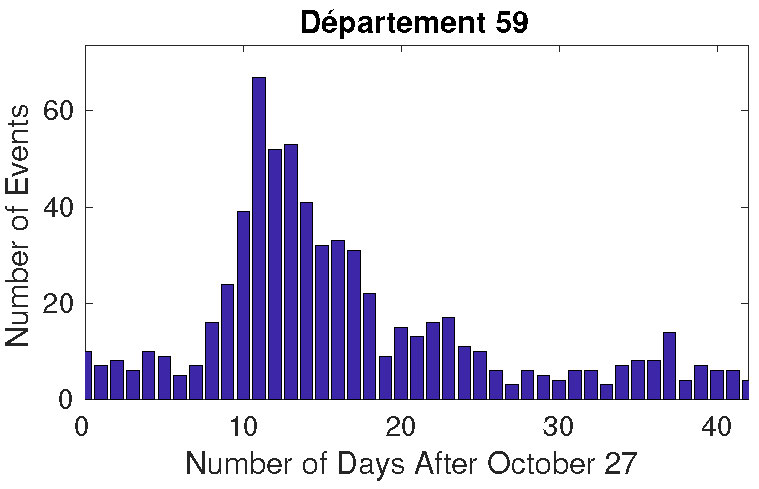
Figure 2. Left: the number of riot-like events on each day after October 27, 2005 in Department 59 of France. Right: the location of Department 59 in the northernmost part of France.
Department 93 may be seen in the bottom left corner of the map in the small group of four unlabeled departments that make up the right inset of Figure 1.
Hence we observe this peak of high activity traveling across France, and this behavior is reminiscent of a traveling wave.
This type of spread is also visible in other rioting events [3, 13].
In fact, planar traveling wave solutions have been observed in numerical simulations for certain parameter regimes for the reaction-diffusion model.
These solutions show a great deal of qualitative variety in terms of their wave speed and monotonicity. Solutions from certain parameter regimes show good agreement
with the spread of rioting behavior observed from the 2005 dataset. An analysis of these traveling wave solutions was performed in [40].
In [40] the existence and stability of traveling wave solutions for the system of partial differential equations was discussed.
The existence and stability of traveling waves that is dependent upon certain parameter values can give us insight into what kinds of conditions and interactions
give rise to traveling waves of rioting behavior. Given that each parameter for the system has a physical representation, we can draw conclusions about what circumstances
cause traveling waves of rioting behavior and what circumstances make that behavior more resilient (stable) to the influence of external forces (for example: policing of riots, etc.).
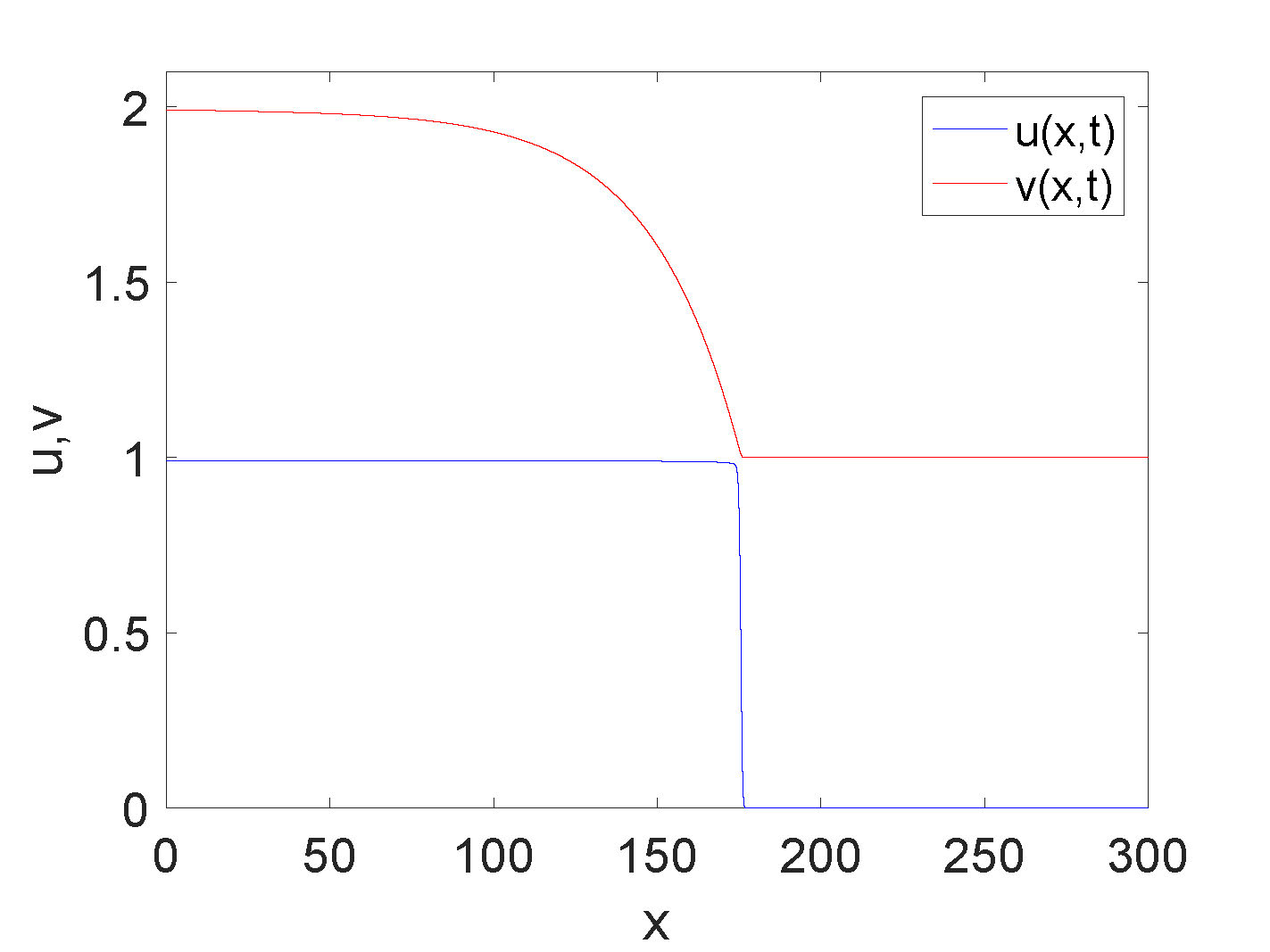
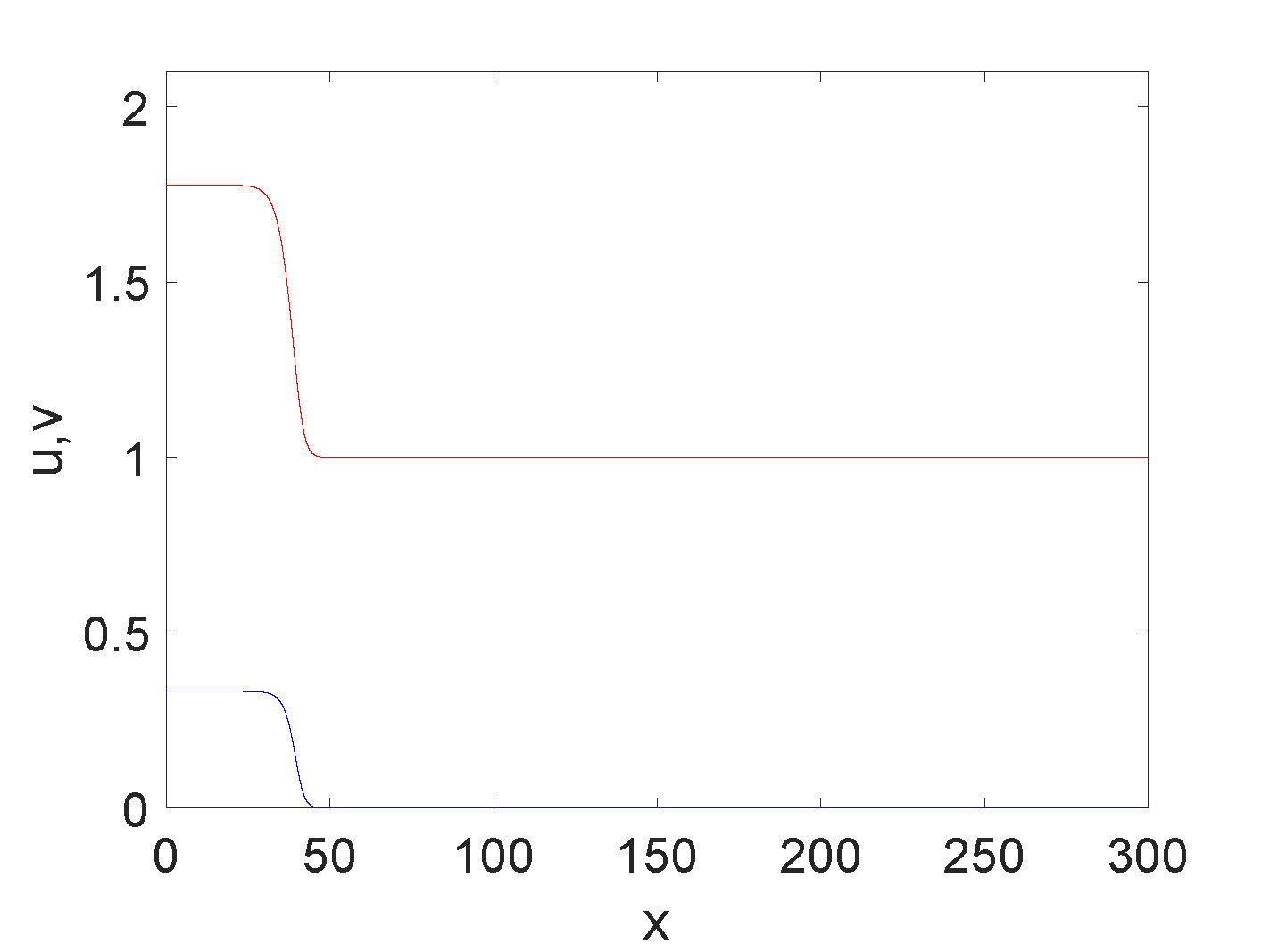
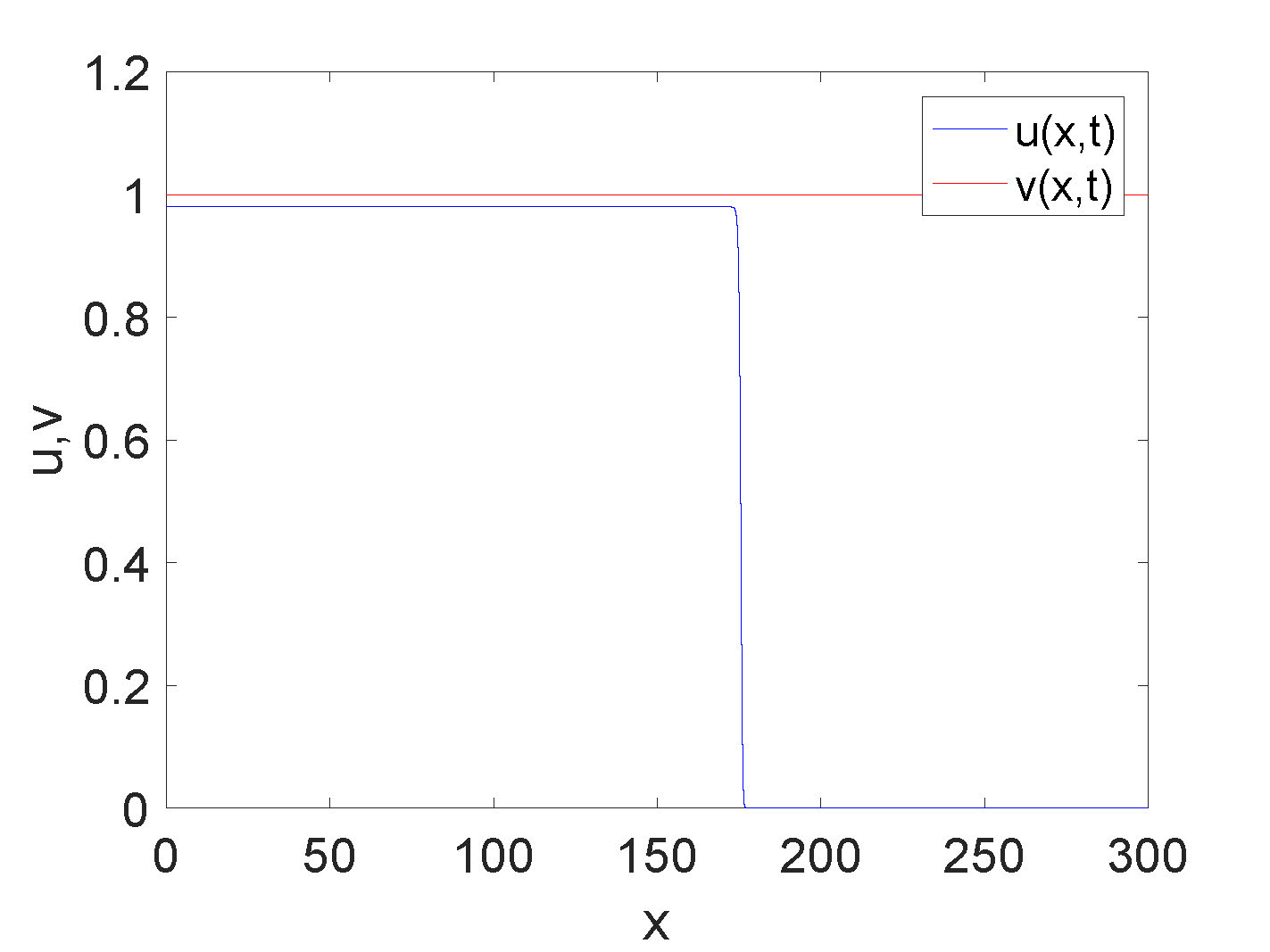
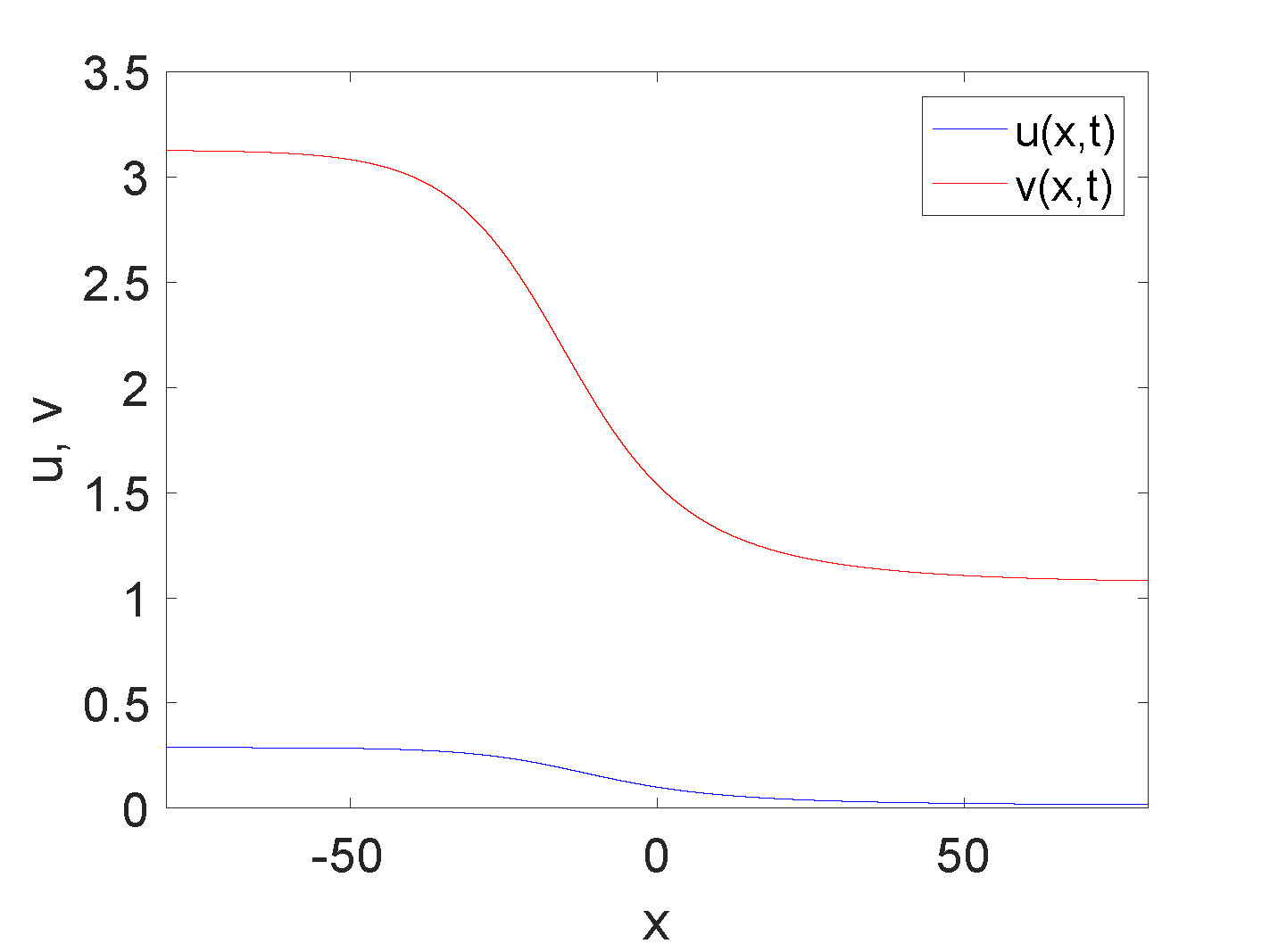
Numerical approximations of solutions have shown clear evidence of traveling wave solutions in three different regimes of monotonicity based on the parameters.
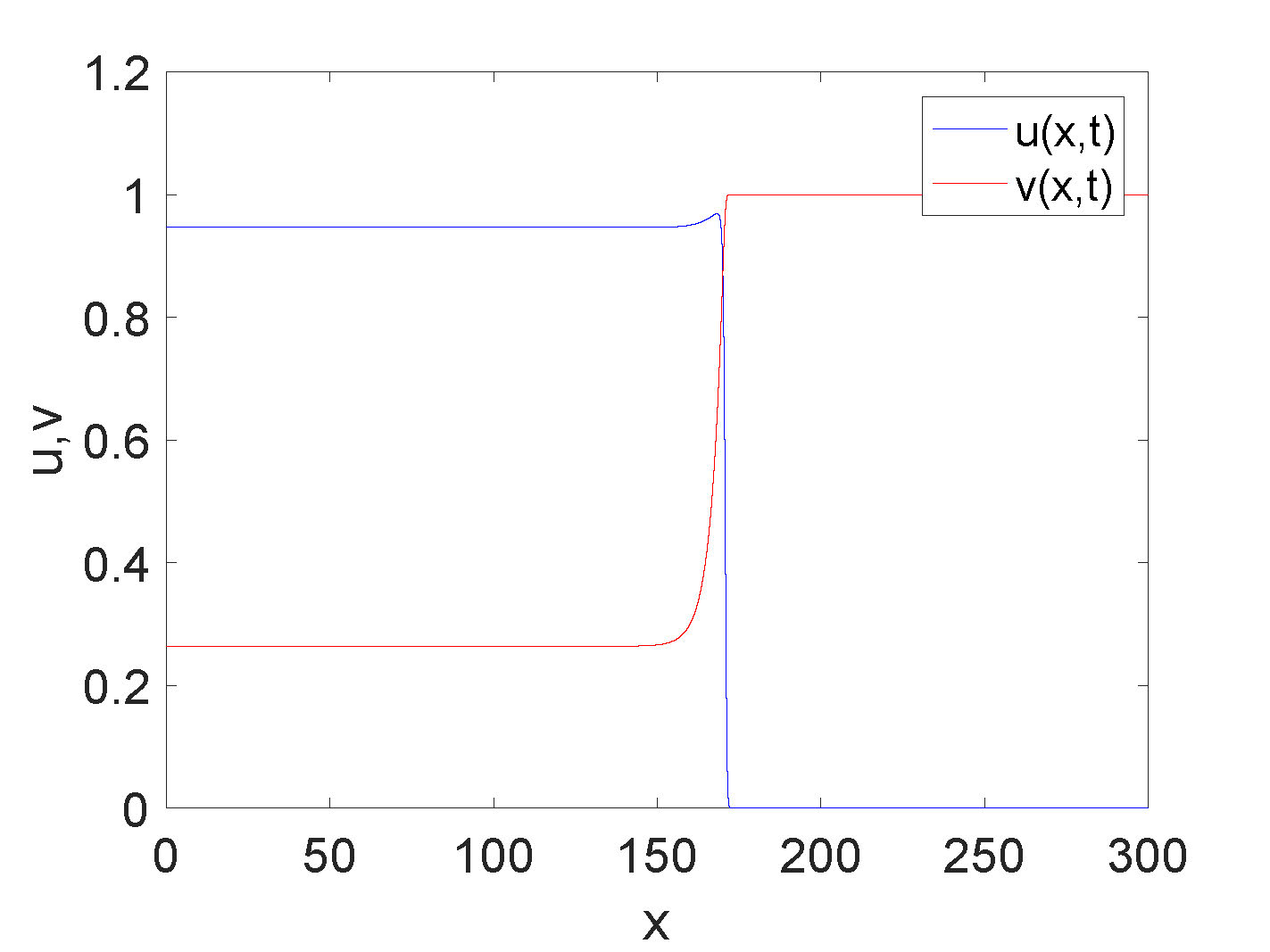
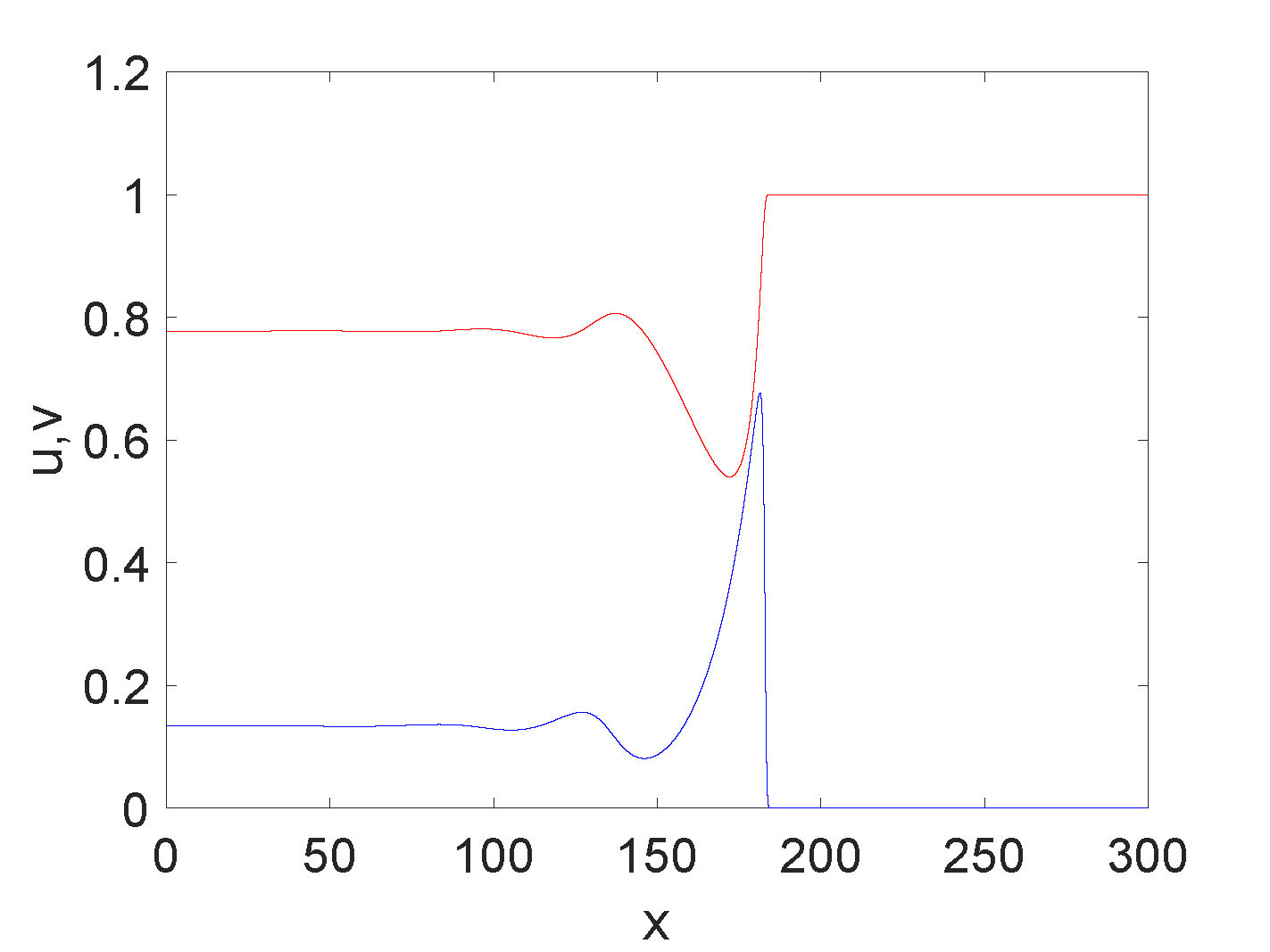
It is observed (and can be proved) that non-monotone waves only exist for \(p<0\). However, the exact dependence on parameters for this behavior is still not well-understood.
Numerical approximations of traveling wave solutions that have been found for \(p<0\) fall into the following categories: 1) a non-monotone traveling wave for \(u\) and a monotone
traveling wave for \(v\), 2) oscillatory waves for both \(u\) and \(v\), and 3) monotone waves for both \(u\) and \(v\). For \(p>0\), monotone traveling waves have been observed numerically for each of the two, three, and four steady state cases.
 |
 |
| (a) \(\Gamma=100\), \(\beta=5\), \(\alpha=1\), and \(p=1\). |
(b) \(\Gamma=1.5\), \(\beta=10\), \(\alpha=1\), and \(p=2\). |
 |
 |
| (c) \(\Gamma=100\), \(\beta=2\), \(\alpha=1\), and \(p=-2\). |
(d) \(\Gamma=100\), \(\beta=20\), \(\alpha=1\), and \(p=-2\). |
 |
 |
| (e) \(p= 0\), \(\Gamma=100\), \(\beta=5\), \(\alpha=1\). |
(f) \(\Gamma = 2.0026\), \(\beta = 0.4021\), \(p=4.5\), \(\alpha = 1\). |
Figure 3. Zoology of traveling wave solutions in various parameter regimes.
For \(p>0\), it is possible to prove the existence and stability of monotone traveling wave solutions for all parameter regimes resulting in the aforementioned two steady state,
monostable and three steady state, bistable systems, using results from [36, 37, 38]. For the four steady state bistable case, the relationship of the steady
states is such that these results are not applicable and further work must be done to establish the existence of the monotone traveling waves observed numerically.
Although the proof of existence of traveling wave solutions for the case \(p<0\) is still an open problem, there is a great deal of numerical evidence for the existence of these waves.
In anticipation of a future proof of existence, it is possible to prove the stability of these waves using a combination of analytic and numerical methods. This involves establishing spectral
stability by linearizing (5) about the traveling wave solution, finding the essential spectrum of the resulting linear operator, and then using numerical computation of
Evans functions to identify the point spectrum [2, 21, 22, 28, 33, 34].
A full presentation of the details of this method and the existence and stability proofs for \(p>0\) are provided in [40].
Remark 1.
For \(p=0\), in the two steady state, monostable case, both steady states have \(v=1\), which is a partial solution for the system. Using this, the system reduces to a partial differential equation in \(u\) that is equivalent to a Fisher-KPP type system [16, 24]. Existence and stability of monotone traveling waves has been well-studied for this system and can be readily established.
In a related work [8], we proposed and studied a data driven epidemiological modeling of this large scale riot episode. Within this framework, the model which best fits the riot propagation is similar to the Kendall epidemics model [23], but with variables living on a discrete set of points (cities) and with heterogeneous populations. This approach allowed us to exhibit the wave, notably in the Paris area where there is a dense tissue of poor neighborhoods. The epidemiological model has also strong similarities with the present reaction-diffusion model: the numbers of infected (rioters) and of susceptible individuals play analogous roles to, respectively, the \(u\) and \(v\) variables. Actually, the idea of considering here \(p<0\) comes from this analogy [7], which is precisely easier to see in the regime \(p<0\), and leads to better data fits. It will be interesting to more systematically explore the correspondence between the epidemiological and reaction-diffusion approaches.
4 Discussion and Open Problems
We have introduced a system of reaction-diffusion equations to model the contagion and spread of rioting activity.
However, we believe that applicability to go beyond rioting activity and can also serve as a model for other social behavior that is
contagious (with potential minor modifications). With regards to the specific model given by system (5)
there are still many open problems which are of interest. To begin with the existence of planar traveling wave solutions
for the case \(p<0\) is currently being worked out. Given the geography of France and the true spread of the activity,
studying the existence of radial traveling waves is of high interest. With regards to the single-site model given by
(1) the convergence to excited cycles in the case \(p<0\) has been observed numerically, but has not been
proved due to the lack of monotonicity. Finally, it would be interesting to prove a phase-transition for stochastic source
term for external shocks.
References
[1] S. Alcaide, Movimiento 15-M: los ciudadanos exigen reconstruir la
política, 2011.
[2] J. Alexander, R. Gardner, and C. Jones, A topological invariant
arising in the stability analysis of travelling waves, Journal fur die Reine und Angewandte Mathematik, 410 (1990), pp. 167–212,
https://doi.org/10.1515/crll.1990.410.167.
[3] P. Baudains, A. Braithwaite, and S. D. Johnson, Spatial Patterns in
the 2011 London Riots, Policing, 7 (2012), pp. 21–31,
https://doi.org/10.1093/police/pas049,
http://policing.oxfordjournals.org/cgi/doi/10.1093/police/pas049.
[4] H. Berestycki, J.-P. Nadal, and N. Rodríguez, A model of riot
dynamics: shocks, diffusion, and thresholds, Networks and Heterogeneous
Media, 10 (2015), pp. 1–34, https://doi.org/10.3934/nhm.2015.10.443.
[5] H. Berestycki and N. Rodríguez, Analysis of a heterogeneous
model for riot dynamics: the effect of censorship of information, European
J. Appl. Math., 27 (2015), pp. 554–582.
[6] H. Berestycki, L. Rossi, and N. Rodríguez, Periodic cycles of
social outbursts of activity, Journal of Differential Equations, 264 (2018), pp. 163–196, https://doi.org/10.1016/j.jde.2017.09.005.
[7] L. Bonnasse-Gahot, Title, In preparation, (2018).
[8] L. Bonnasse-Gahot, H. Berestycki, M.-A. Depuiset, M. B. Gordon, J.-P. Nadal, S. Roché, and N. Rodríguez, Epidemiological modelling of the 2005 French riots: a spreading wave and the role of
contagion, Scientific Reports, 8 (2018).
[9] J.-P. Bouchaud, C. Borghesi, and P. Jensen, On the emergence of an "intention field" for socially cohesive agents, Journal of Statistical
Mechanics: Theory and Experiment, 2014 (2014), pp. 1–10,
http://arxiv.org/abs/1311.0810v2,
https://arxiv.org/abs/1311.0810.
[10] D. Braha, Global civil unrest: contagion, self-organization, and
prediction, PloS One, 7 (2012), pp. 1–9,
https://doi.org/10.1371/journal.pone.0048596,
http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3485346&tool=pmcentrez&rendertype=abstract.
[11] C. Cazelles, B. Morel, and S. Roché, Les violences urbaines
de l'automne 2005: événements, acteurs: dynamiques et interactions. Essai de synthèse, Centre d'analyse stratégique, (2007).
[12] R. Crane and D. Sornette, Robust dynamic classes revealed by
measuring the response function of a social system, Proceedings of the
National Academy of Sciences of the United States of America, 105 (2008),
pp. 15649–53, https://doi.org/10.1073/pnas.0803685105,
http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2572957&tool=pmcentrez&rendertype=abstract.
[13] T. P. Davies, H. M. Fry, A. G. Wilson, and S. R. Bishop, A
mathematical model of the London riots and their policing, Scientific
Reports, 3 (2013), pp. 1–9, https://doi.org/10.1038/srep01303,
http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3578270&tool=pmcentrez&rendertype=abstract.
[14] M.-A. Depuiset, M. B. Gordon, J.-P. Nadal, and S. Roché, Database on the number of rioting events during the 2005 French riots.
[15] T. Economists, The BlackBerry riots, The Economists, (2011).
[16] R. A. Fisher, The wave of advance of advantageous genes, Ann.
Eugenics, 7 (1937), pp. 353–369, https://doi.org/10.1111/j.1469-1809.1937.tb02153.x.
[17] M. W. Flamm, Law and order: Street crime, civil unrest, and the
crisis of liberalism in the 1960s, Columbia University Press, 2005.
[18] S. González-Bailón, J. Borge-Holthoefer, A. Rivero, and
Y. Moreno, The dynamics of protest recruitment through an online
network, Scientific Reports, 1 (2011), pp. 1–7,
https://doi.org/10.1038/srep00197,
http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3240992&tool=pmcentrez&rendertype=abstract.
[19] D. Goodman and A. Baker, Wave of protests after grand jury doesn't indict officer in Eric Garner chokehold case, The New York Times, December 3 (2014).
[20] M. Gordon, J.-P. Nadal, D. Phan, and V. Semeshenko, Discrete
Choices under Social Influence: Generic Properties, Mathematical Models and
Methods in Applied Sciences (M3AS), 19 (2009), pp. 1441–1481,
https://arxiv.org/abs/0704.2333.
[21] K. Harleya, P. Van Heijstera, R. Marangellb, G. J. Petteta, and
M. Wechselbergerb, Numerical computation of an evans function for
travelling waves, Mathematical Biosciences, 266 (2015), pp. 36–51,
https://doi.org/10.1016/j.mbs.2015.05.009,
https://arxiv.org/abs/1312.3685.
[22] T. Kapitula and K. Promislov, Spectral and Dynamical Stability of
Nonlinear Waves, Springer, 2013.
[23] D. G. Kendall, Mathematical models of the spread of infection,
Mathematics and computer science in biology and medicine, (1965), pp. 213–225.
[24] A. M. Kolmogorov, I. Petrovskii, and N. Piskunov, A study of the
diffusion equation with increase in the amount of substance, and its
application to a biological problem, Selected works of AN Kolmogorov, 6
(1991), pp. 1–26, http://link.springer.com/chapter/10.1007/978-94-011-3030-1_38.
[25] J. Lang and H. De Sterck, The Arab Spring: a simple compartmental
model for the dynamics of a revolution, Mathematical Social Sciences, 69
(2014), pp. 12–21, https://doi.org/10.1016/j.mathsocsci.2014.01.004,
http://linkinghub.elsevier.com/retrieve/pii/S0165489614000055.
[26] W. Lowery, C. D. Leonnig, and M. Berman, Even before Michael
Brown's slaying in Ferguson, racial questions hung over police, 2014.
[27] M. Lynch, The Arab Uprising The Unfinished Revolutions Of The New
Middleeast, Public Affairs, New York, first ed.
[28] J. L. Marzuola and G. Simpson, Spectral analysis for matrix
hamiltonian operators, Nonlinearity, 24 (2011), pp. 389–429,
https://doi.org/10.1088/0951-7715/24/2/003.
[29] G. O. Mohler, M. B. Short, P. J. Brantingham, F. P. Schoenberg, and G. E.
Tita, Self-Exciting Point Process Modeling of Crime, Journal of the American Statistical Association, 106 (2011), pp. 100–108,
https://doi.org/10.1198/jasa.2011.ap09546,
http://www.tandfonline.com/doi/abs/10.1198/jasa.2011.ap09546.
[30] B. Moore, Injustice: The Social Bases of Obedience and Revolt,
White Plains, New York, 1978.
[31] Y. Ogata, Space-time point-process models for earthquake
occurrences, Annals of the Institute of Statistical Mathematics, 50 (1998),
pp. 379–402, http://link.springer.com/article/10.1023/A:1003403601725.
[32] R. Pego and M. Weinstein, Eigenvalues, and instabilities of
solitary waves, Philosophical Transactions: Physical Sciences and Engineering, 340 (1992), pp. 47–94.
[33] B. Sandstede and A. Scheel, Absolute and convective instabilities
of waves on unbounded and large bounded domains, Physica D, 145 (2000),
pp. 233–277, https://doi.org/10.1016/S0167-2789(00)00114-7,
https://scinapse.io/papers/2122013064.
[34] D. H. Sattinger, On the stability of waves of nonlinear parabolic
systems, Advances in Mathematics, 22 (1976), pp. 312–355, https://doi.org/10.1016/0001-8708(76)90098-0.
[35] M. B. Short, M. R. D'Orsogna, V. B. Pasour, G. E. Tita, P. J. Brantingham,
A. Bertozzi, and L. B. Chayes, A statistical model of criminal behavior, Math. Models Methods Appl. Sci., 18 (2008), pp. 1249–1267, http://www.worldscientific.com/doi/pdf/10.1142/S0218202508003029.
[36] A. I. Vol'pert and V. A. Vol'pert, Application of the theory of the
rotation of vector fields to the investigation of wave solutions of parabolic
equations, Trudy Moskov. Mat. Obshch., 52 (1989), pp. 58–109,247.
[37] A. I. Volpert, V. A. Volpert, and V. A. Volpert, Traveling Wave
Solutions of Parabolic Systems, American Mathematical Society, Providence,
RI, 140 ed., 1994.
[38] V. Volpert, Reaction-diffusion waves: classical theory and recent
developments, (2008), pp. 1–28.
[39] J. K. Walton and D. Seddon, Free Markets and Food Riots: The
Politics of Global Adjustment, Wiley-Blackwell, 1994.
[40] C. Yang, Analysis of Monotone and Non-monotone Traveling Waves in a System for Social Outbursts, UNC Chapel Hill, 2018.