P.G. Kevrekidis,
Department of Mathematics and Statistics, University of Massachusetts,
Amherst MA 01003-4515, USA
R. Carretero-González,
Nonlinear Dynamical System Group (NLDS),
Computational Science Research Center, and
Department of Mathematics and Statistics,
San Diego State University,
San Diego, California 92182-7720, USA
D.J. Frantzeskakis,
Department of Physics, University of Athens, Panepistimiopolis,
Zografos,
Athens 157 84, Greece
Abstract:
In this brief exposition, we showcase some recent experimental and theoretical work
in the coldest temperatures in the universe involving topological
defects (vortices) in the newest state of matter: the atomic Bose-Einstein condensates.
The remarkable feature that these experiments and associated analysis
illustrate is the existence of a new kind of ``classical mechanics''
for
vortices, which revisits the integrability of the
two-body (i.e., two-vortex) system and opens up exciting extensions
for
N-body generalizations thereof. One-dimensional and three-dimensional
analogues of such dynamics, involving dark solitons and vortex rings,
respectively, are also briefly touched upon.
The General Setting: Bose-Einstein Condensates and Vortex Emergence
The phenomenon of Bose-Einstein condensation [1,2,3]
is a quantum phase transition originally predicted in 1924.
In particular, it was shown that below a critical transition temperature
Tc
a macroscopic fraction of particles of a boson gas (i.e., whose particles obey the Bose statistics) condenses
into the same quantum state, known as the Bose-Einstein condensate (BEC).
Despite the fundamental nature of this prediction,
BECs were not experimentally realized until 70 years later:
this major achievement took place in 1995 and has already been recognized
through the 2001 Nobel Prize in Physics [4].
This first unambiguous manifestation of a macroscopic quantum state in a
many-body system
sparked an explosion of activity, as reflected by the publication of several
thousand papers
related to BECs since then. Nowadays there exist more than fifty experimental
BEC groups around
the world, while an enormous amount of theoretical work has followed and driven
the experimental efforts, with an impressive impact on many branches of
Physics.
From a theoretical standpoint, and for experimentally relevant conditions, the
static and dynamical properties of a BEC can be described by means of an effective
mean-field model, namely a partial differential equation (PDE) known as the Gross-Pitaevskii
equation (GPE). This is actually a
nonlinear Schrödinger (NLS) equation [5]
of the form:
where
Ψ = Ψ(r,t)
is the macroscopic wavefunction of the condensate
(the atomic density is proportional to
|Ψ(r,t)|2),
Δ is the Laplacian,
m is the atomic mass,
and the prefactor
g is proportional to the atomic scattering
length and describes the interatomic interactions [6,7]
(the latter may be repulsive,
\(g > 0\), e.g., for
87Rb and
23Na atoms, or attractive,
g < 0, e.g., for
85Rb or
7Li atoms).
The external potential
Vext is used to confine the atoms and, usually, has
a harmonic (parabolic) form.
| $$\displaystyle i \hbar \frac{\partial\Psi}{\partial t}=-\frac{{\hbar}^2}{2 m} \Delta \Psi + g \vert\Psi\vert^2 \Psi + V_{{\rm ext}} ({\bf r}) \Psi,$$
|
(1) |
One of the remarkable features of this GPE-based mean-field approach
is that it allows the prediction and description of
coherent
macroscopic excitations that can be supported in BECs due to
the interatomic-interaction-induced
nonlinearity in Eq. (1).
Relevant ``nonlinear matter-waves'' include bright, dark and gap solitons,
as well as vortices and vortex lattices [6,7].
The present discussion will especially focus on
vortices whose profound implications in fundamental physical phenomena, such as
superconductivity and superfluidity, were also recognized by the
Nobel Prize in Physics in 2003 [8].
Vortices are ubiquitous circulating flow patterns that arise in numerous
contexts [9], ranging
from hydrodynamics, superfluids, and nonlinear optics to specific
realizations in sunspots, dust devils [10], and plant
propulsion [11]. In BECs, quantized vortices arise as
persistent topological defects that have a key role in both
Hamiltonian and dissipative dynamics, as well as in quantum turbulence. The
relevance of such individual coherent topological structures, as well as of
large scale lattices thereof, has been analyzed in a series of
specialized reviews [12,13,14]. It should
be noted here that while vortices can arise in
BECs with attractive inter-atomic interactions
(g < 0),
their instability towards catastrophic
collapse-type events renders them less robust therein. We will thus, hereafter, focus
on condensates with repulsive interactions
(g > 0),
where vortices are very robust.
A Special Case of Particular Interest: The Vortex Dipole
In the case of repulsive ``pancake''-shaped BECs confined in strongly-anisotropic
(quasi-two-dimensional) harmonic traps,
a single vortex has relatively simple dynamics: if placed at the center
of the trap, it can be identified as a stationary mode of the nonlinear system
of Eq. (1). On the other hand, if placed off-center, it
does what a (topologically) charged particle does in a magnetic
field: it precesses with frequency
Ω.
Matched asymptotics [12] can be
used to obtain this precession frequency near the center of the trap, as well as
its logarithmic dependence on the trap strength and on the
chemical potential
(the latter, pertains to the strength
of the nonlinearity or, physically, the number of atoms of the BEC).
Figure 1 shows
an example of such a stationary vortex and of its precessional
space-time (off-center) dynamics. Notice that this bears a direct analogy
to the simple oscillatory dynamics of a single dark soliton (a one-dimensional
density dip) in quasi-one-dimensional, ``cigar''-shaped BECs [15].
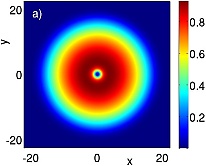
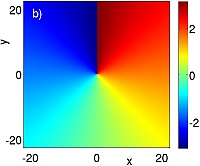
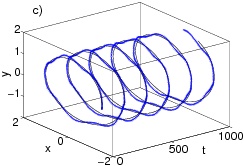
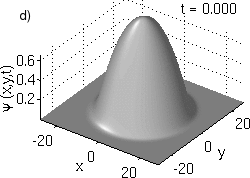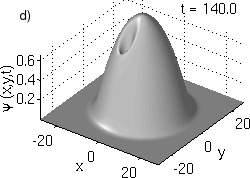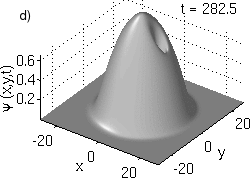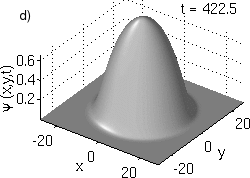
Figure 1:
Prototypical example of the a) amplitude
and b) phase profiles of a trapped vortex at the center of a parabolic trap.
c)
(x,y,t)
dynamics for an off-center precessing vortex from the full GPE
(1) (blue points) and the reduced ODE model (2)
(thin black line). d) Animation of the evolution of the density for a precessing vortex.
|
|
Things get far more interesting when considering the evolution of
two (or more) vortices. Then, each vortex has its own precessional
dynamics, but importantly there also exists the pairwise vortex interaction
which can be thought of as a Hamiltonian fluid point vortex
interaction [16]. The resulting (reduced) dynamical set of ordinary
differential equations (ODEs)
of motion characterizing the center positions
(xk,yk)
of
N interacting vortices reads:
|
$$\displaystyle i\dot{z}_k = - S_k\, \Omega(r_k) z_k + A\sum_{j\neq k}^N S_j \frac{z_k-z_j}{r_{jk}^2},$$
|
(2) |
where
zk = xk + iyk
= rk eiθk,
rk = |zk|
and
rjk = |zk-zj|.
In Eq. (2) the topological charge of the
k-th vortex is
Sk = ± 1,
with the positive (negative) sign referring to counterclockwise (clockwise) circulation
as viewed from the positive
z
axis. Also, the precession frequency that can be accurately
approximated by
\(\Omega(r_k) = \Omega_0/(1-r_k^2/R^2)\)
(for \(r_k < R\)) depends on the spatial location
of the vortex [12,14], where
R denotes the spatial
extent of the BEC and
Ω0 is the (spatially independent)
precession frequency value at the center of the BEC,
while
A is a
constant prefactor that accounts for the spatial inhomogeneity of
the BEC [17].
While the above equations describe an arbitrary number of trapped
vortices, the case of two opposite charge (i.e., counter-rotating)
vortices, i.e., a vortex dipole, is especially motivated by a series of recent
experiments. In these experiments, dipoles were produced
either by dragging an obstacle through
the BEC [18] (a superfluid analog of the classic
flow-past-a-cylinder experiment), or by quenching rapidly through the
quantum phase transition (trapping phase singularities in the process) [19,20]
in what is known as the Kibble-Zurek mechanism.
The case of two vortices is especially interesting as it forms
a four-degree-of-freedom Hamiltonian system, in which -in addition
to the standard conservation law of the energy- also the angular
momentum
is conserved [21].
The presence of two conserved quantities or dynamical invariants guarantees integrability in the classical Liouville
sense for the case
N=2, whether the vortices are co- or counter-rotating.
This implies that the energy level sets are compact and the phase space is
foliated by invariant tori. On each of these, the motion is generically quasi-periodic
with two frequencies. In the following, we consider further
dynamical aspects of the
N=2 case for vortex dipoles with
S1 = - S2 = 1.
In particular, since the precession tends to rotate each vortex in one
direction, while their mutual interaction yields an opposite
tendency, an equilibrium distance of the dipole can be identified in
excellent agreement between the above particle ODE picture (2)
and the experiment [20]. In some sense, this ``zero frequency''
equilibrium state is the simplest (non-generic)
dynamical scenario among the possible vortex
dipole motions. The immediately next (still non-generic)
scenario in terms of complexity
pertains to a ``single frequency'' motion: such an internal mode of the
two-vortex system can also be identified by linearizing around the
above equilibrium. It corresponds to an epicyclic precession of the vortices
around the equilibrium that was also observed in experiments
(see Fig. 2) again in good agreement with the theoretical
predictions [20].
Figure 2:
Panel a) depicts experimental data snapshots for the epicyclic precession
of two vortices as a function of time (indicated by the different colors).
The data are assembled into a trajectory in panel b): the experimental
vortex locations are given by triangles, while the theoretical predictions
for the same times are shown by circles (of the same color). The underlying
theoretical trajectory is given by the solid line.
Adapted from Ref. [20].
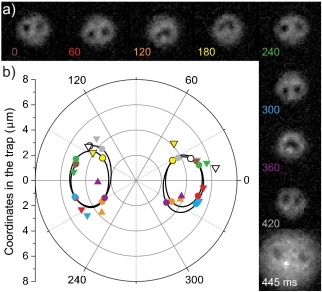
|
Finally, the typical scenario in this dipole setting concerns
quasi-periodic (generic) motions. Namely, when two frequencies are involved
in the motion of each vortex, we see the more complicated either
``epitrochoidal'' motions of the top panel, or the outer fast
precession and inner flower-like motions of the middle and bottom
panels of Fig. 3. All of these orbits, however, in the proper
co-rotating frame result in closed orbits revealing the quasi-periodic
character of the motion. In fact, although the particle dynamics is
integrable, the underlying full experimental system to which it is
compared can be thought of as a weakly non-integrable (infinite
degrees of freedom) generalization thereof. As such, the observed
identification of quasi-periodic orbits can be thought of as
an experimental manifestation of KAM theory. It should also
be mentioned in passing that this class of particle models
parallels the understanding now reached in the case of
the oscillations and interactions of the one-dimensional analogues of
vortices, namely the dark solitons [15]. There, a model
in the form of a Toda lattice on the relative positions between
adjacent dark solitons (dark soliton interactions)
embedded in a harmonic trap (effect from the parabolic trapping
on each dark soliton):
|
$$\displaystyle \ddot{a}_j = -\frac{1}{2}\, \omega_{\rm trap}^2\, a_j - 8\, \mu^{3/2}\left( \exp(-2\sqrt{\mu }(a_{j+1}-a_j)) - \exp(-2\sqrt{\mu} (a_j-a_{j-1})) \right).$$
|
(3) |
can be used to characterize the orbits of the interacting dark
solitons as a function of system parameters (such as the effective
strength of the parabolic trap
ωtrap
and chemical potential μ).
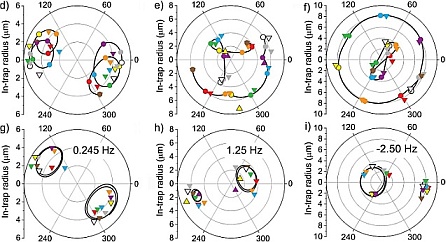
Figure 3:
Same as in the previous figure for 3 different trajectories a), b), c)
which are generic examples of the two-frequency dynamics of the vortices.
Panels d), e), f) summarize the vortex motions and illustrate (together
with a), b) and c)) the agreement between ODEs and experiment. Panels
g), h) and i) explicitly
showcase the quasi-periodic nature of these motions, by
virtue of displaying the dynamics in a proper co-rotating frame
(whose rotational frequency is indicated in each panel).
Adapted from Ref. [20].

|
|
Generalizations and (Many) Open Avenues
Although the vortex dipole is gradually becoming a more charted
territory and provides the fundamental modeling background for
tackling more complex settings, in practice there is a tremendous
amount of open problems that are shaping up within this field,
as stemming from its novel ``classical mechanics'' of these
interacting vortex particles (or, for that matter, the
interacting dark soliton particles). Perhaps the simplest such
issue consists
of the co-rotating vortex pair which, although integrable, has
been recently shown to possess an instability of its prototypical
configuration of two equi-distantly rotating vortices (with respect
to the center of the trap). An interesting symmetry-breaking
bifurcation already seems to arise therein.
Going beyond
N=2 vortex (or soliton) dynamics breaks
the integrability and poses exciting challenges in its own
right. Are there chaotic trajectories, (analogues of)
Lagrangian points and other interesting features reminiscent
of classical 3-body problems of classical mechanics ?
It should be noted here that 3-vortex states have also
been identified in experiments in either co-rotating or
counter-rotating sets of clusters in the very recent experiments
of Ref. [22], hence there is a significant interest
towards their detailed understanding. Generalizing notions to
N-body problems, e.g., identifying special equilibrium configurations,
examining their stability, and the near equilibrium (or far
from equilibrium) dynamics, as well as studying possible
periodic orbits tantamount to the periodic choreographies
(cf., figure-eight
N-planet orbits) found
in celestial mechanics [23,24], constitute further
exciting frontiers
in these explorations. An additional frontier concerns the
transitions of this system from the near-equilibrium
soliton/vortex-solid to the far-from-equilibrium soliton/vortex
gas and the potentially turbulent dynamics that the latter
may possess. Clearly this dynamics is beyond the above
particle picture and should be considered at the level
of the full PDE of Eq. (1) and, most likely, of
its dissipative generalizations pertinent to finite
temperature BECs.
Such issues are starting
to be explored in both the theoretical and experimental
literature of BECs and may produce an exciting framework
for exploring, among others, superfluid quantum turbulence.
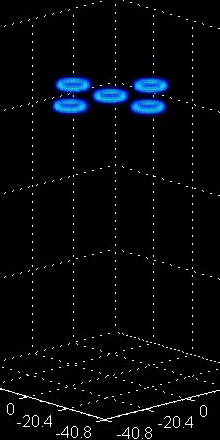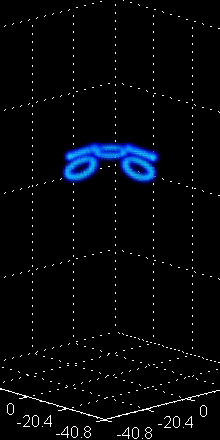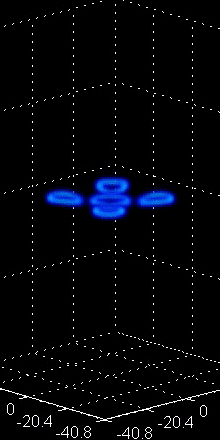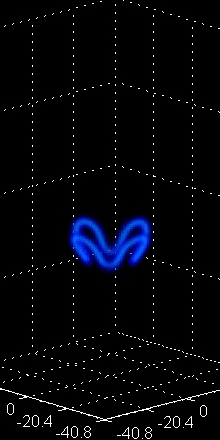
Figure 4:
Vortex ring interactions, mergers and breakups.
The left animation depicts two vortex rings
chasing each other in a ``leap-frog'' orbit.
The middle animation depicts four co-planar vortex rings
that attract each other, merge and in the process
shoot a fifth vortex ring in the opposite direction.
The right animation depict the periodic merger
and breakup of five co-planar vortex rings.
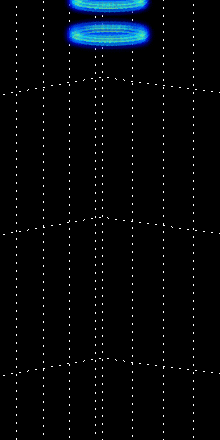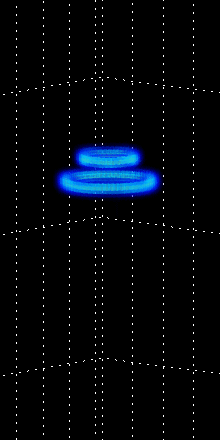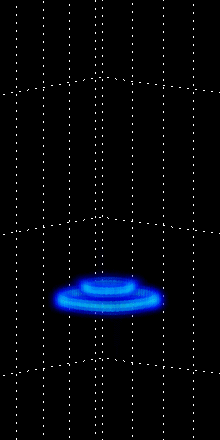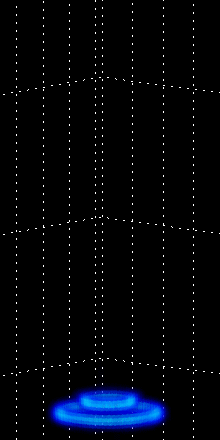

|
Finally, while two-dimensions already afford the possibility
for topological charges, the fully three-dimensional setting
enables the consideration of far more complex fundamental
entities than the line-vortex generalizations of our
two-dimensional vortices
above, namely the study of vortex rings. These coherent structures
also possess fascinating dynamics including leap-frogging
orbits between two vortex rings and remarkable merger and
breakup events in the case of more rings (see Fig. 4
for some animated examples). Developing a particle
picture and analyzing the full
three-dimensional PDE evolution pose exciting
tasks not only for experiments and theory, but even for numerical
implementations thereof.
Acknowledgments
We would like to acknowledge our colleagues D.S. Hall, D.V. Freilich,
S. Middelkamp, P.J. Torres, P. Schmelcher, and R. Navarro
for their contribution towards this ongoing collaboration.
We also thank R.M. Caplan for the vortex ring simulations and
NSF-DMS-0806762 and the Special Account for Research Grants of the University of
Athens for financial support.
References
| [1] |
|
F. Dalfovo, S. Giorgini, L.P. Pitaevskii and S. Stringari,
Theory of Bose-Einstein condensation in trapped gases,
Rev. Mod. Phys. 71 (1999) 463-512.
|
| [2] |
C.J. Pethick and H. Smith,
Bose-Einstein condensation in dilute gases,
Cambridge University Press (Cambridge, 2002).
|
| [3] |
L.P. Pitaevskii and S. Stringari,
Bose-Einstein Condensation, Oxford University Press (Oxford, 2003).
|
| [4] |
http://www.nobelprize.org/nobel prizes/physics/laureates/2001/
|
| [5] |
C. Sulem and P.L. Sulem,
The Nonlinear Schrödinger Equation
(Springer-Verlag, New York, 1999).
|
| [6] |
P.G. Kevrekidis, D.J. Frantzeskakis, and R. Carretero-González Emergent Nonlinear
Phenomena in Bose-Einstein Condensates: Theory and Experiment.
Springer Series on Atomic, Optical, and Plasma Physics, Vol. 45 (2008).
|
| [7] |
R. Carretero-González,
D.J. Frantzeskakis and P.G. Kevrekidis,
Nonlinear waves in Bose-Einstein condensates: physical relevance and mathematical techniques,
Nonlinearity 21 (2008) R139-R202.
|
| [8] |
http://www.nobelprize.org/nobel prizes/physics/laureates/2003/
|
| [9] |
L.M. Pismen, Vortices in Nonlinear Fields
(Clarendon, UK, 1999).
|
| [10] |
H.J. Lugt, Vortex Flow in Nature and Technology
(Wiley, New York, 1983).
|
| [11] |
D.L. Whitaker and J. Edwards, Science 329
406 (2010).
|
| [12] |
A.L. Fetter and A.A. Svidzinsky, J. Phys.:
Condens. Matter 13, R135 (2001).
|
| [13] |
P.G. Kevrekidis, R.
Carretero-González, D.J. Frantzeskakis and I. Kevrekidis,
Mod. Phys. Lett. B 18, 1481 (2004).
|
| [14] |
A.L. Fetter, Rev. Mod. Phys. 81, 647 (2009).
|
| [15] |
D.J. Frantzeskakis, J. Phys. A: Math. Theor.
43, 213001 (2010).
|
| [16] |
A.J. Chorin and J.E. Marsden,
A Mathematical Introduction to Fluid Mechanics
(Springer-Verlag, New York, 1993).
|
| [17] |
P.J. Torres, P.G. Kevrekidis, D.J. Frantzeskakis,
R. Carretero-González, P. Schmelcher, and D. S. Hall,
Phys. Lett. A 375, 3044 (2011).
|
| [18] |
T.W. Neely, E.C. Samson, A.S. Bradley, M.J. Davis and
B.P. Anderson, Phys. Rev. Lett. 104, 160401 (2010).
|
| [19] |
D.V. Freilich, D.M. Bianchi, A.M. Kaufman,
T.K. Langin and D.S. Hall, Science 329, 1182 (2010).
|
| [20] |
S. Middelkamp, P. J. Torres, P. G. Kevrekidis,
D. J. Frantzeskakis, R. Carretero-González, P. Schmelcher, D. V.
Freilich, and D. S. Hall
Phys. Rev. A 84, 011605 (2011)
|
| [21] |
P.K. Newton and G. Chamoun, SIAM Rev. 51,
501 (2009).
|
| [22] |
J.A. Seman, E.A.L. Henn, M. Haque, R.F. Shiozaki, E.R.F. Ramos, M. Caracanhas, P. Castilho, C. Castelo Branco, P.E.S. Tavares and F.J. Poveda-Cuevas, G. Roati, K. M. F. Magalhaes, and V. S. Bagnato,
Phys. Rev. A 82, 033616 (2010).
|
| [23] |
A. Chenciner, R. Montgomery,
Ann. Math., 152 (2000) 881-901.
|
| [24] |
http://blogs.discovermagazine.com/cosmicvariance/2006/07/23/n-bodies/
|
| Author Institutional Affiliation | P. G. Kevrekidis,
Department of Mathematics and Statistics, University of Massachusetts,
Amherst MA 01003-4515, USA
R. Carretero-González,
Nonlinear Dynamical System Group (NLDS), Computational Science Research Center, and Department of Mathematics and Statistics, San Diego State University,
San Diego, California 92182-7720, USA
D. J. Frantzeskakis,
Department of Physics, University of Athens, Panepistimiopolis, Zografos,
Athens 157 84, Greece |
| Author Email | kevrekid(at)math.umass.edu, rcarretero(at)mail.sdsu.edu, and dfrantz(at)cc.uoa.gr |
| Tutorial Level | Basic Tutorial |
| Description | Presentation |
| Contest Entry | No |