In this entry M. Dellnitz, S. Klus, and A. Ziessler summarize an article that they recently published in SIAM Journal on Applied Dynamical Systems [1].
Analyzing the influence of uncertainties in complex dynamical systems on the system's behavior has gained considerable attention in the last years. Our goal is to quantify the effects of such uncertainties and their impact on, for instance, stability or performance of the system from a global point of view. We consider in particular parameter-dependent discrete dynamical systems of the form
\begin{equation*}
x_{j+1} = f(x_j,\lambda), \quad j = 0, 1, \dots,
\end{equation*}
where \(\lambda \in \Lambda \subset \mathbb{R}^p \) contains the uncertain parameters, and define a corresponding (set-valued) map
\begin{equation*}
F_\Lambda(x) = f(x,\Lambda).
\end{equation*}
We then compute an approximation of the so-called \((Q,\Lambda)\)-attractor, given by
\begin{equation*}
A_{Q,\Lambda} = \bigcap_{j\ge 0} F_\Lambda^j(Q).
\end{equation*}
\(A_{Q,\Lambda}\) contains all of state space which could potentially be reached under specific uncertainty distributions supported on the parameter space \(\Lambda\). In our approach we cover \(A_{Q,\Lambda}\) by outer approximations using a multilevel subdivision scheme comprising two main steps:
- Subdivision: Subdivide each box into smaller boxes.
- Selection: Keep only those boxes which contain parts of the attractor.
By repeatedly carrying out this procedure, we generate a sequence of box coverings whose size converges to zero. The numerical complexity of the subdivision method depends crucially on the dimension of \(A_{Q,\Lambda}\). Our experience indicates that we can approximate these objects for dimensions up to three even in higher-dimensional state space. On the other hand, it will become very time-consuming to compute \(A_{Q,\Lambda}\) if its dimension is larger than four.
Once \(A_{Q,\Lambda}\) is known the invariant measure corresponding to a specific choice of parameter uncertainty is computed via a transfer operator approach [2]. More precisely, based on the coverings of \(A_{Q,\Lambda}\) we use Ulam's method to construct a corresponding Markov chain and compute its stationary distribution as an approximation of the invariant measure.
We illustrate our method with an example. Let us consider the Arneodo system
\begin{align*}
\dot x_1 &= x_2,\\
\dot x_2 &= x_3,\\
\dot x_3 &= -x_3 -2x_2+\lambda x_1 -x_1^2.
\end{align*}
This system possesses the equilibria \(\widetilde X_1 = (0,0,0)\) and \(\widetilde X_2(\lambda) = (\lambda,0,0)\). The latter is asymptotically stable for \(\lambda < 2\). At \(\lambda = 2\), the equilibrium \(\widetilde X_2(\lambda)\) undergoes a supercritical Hopf bifurcation. For \(\lambda > 2\), points on the two-dimensional unstable manifold of \(\widetilde X_2(\lambda)\) converge to the corresponding limit cycle on the branch of periodic solutions, where the amplitude of the limit cycle grows with increasing values of \(\lambda\). For \(\lambda \approx 3.1\), the limit cycle loses its stability in a period-doubling bifurcation.

The first video (subdivision.avi) shows the subdivision process described above. Here, we chose \( \Lambda=[2.8,3.4] \subset \mathbb{R} \) and define \( f(x, \lambda) \) to be the time-\( T \)-map \( \phi^T(x,\lambda) \) with \( T = 2 \), where \( \phi \) is the flow associated with the Arneodo system.
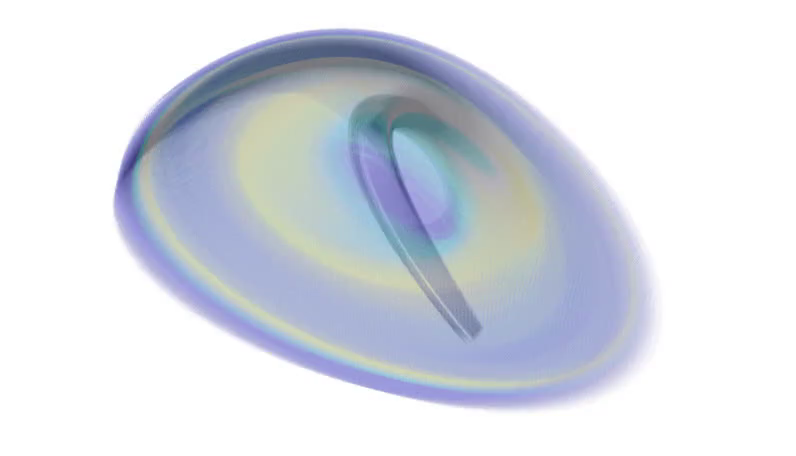
The second video (
invariant_measure.avi) shows the computed invariant measure for the initial density \( \lambda \sim \mathcal{N}(3.1, 0.01) \), where \( \mathcal{N}(\mu,\sigma^2)\) denotes a normal distribution with mean \( \mu \) and variance \( \sigma^2 \). The density ranges from blue (low density) \( \rightarrow \) green \( \rightarrow \) yellow (high density).
References
[1] M. Dellnitz, S. Klus, and A. Ziessler. A set-oriented numerical approach for dynamical systems with parameter uncertainty. SIAM Journal on Applied Dynamical Systems, 16(1):120--138, 2017. DOI. 10.1137/16M1072735
[2] M. Dellnitz and O. Junge. On the Approximation of Complicated Dynamical Behavior. SIAM Journal on Numerical Analysis, 36:491--515, 1999. DOI:10.1137/S0036142996313002