Actin is an abundant and highly dynamic protein inside cells. The actin cytoskeleton is a network of actin filaments which can reorganize significantly during cell migration or throughout the cell cycle, transitioning between open patches, homogeneous meshes, bundles, and circular ring channels. This dynamic reorganization relies on the interaction of actin filaments with several types of myosin motor proteins, described by different kinetic parameters. While other proteins and changes in the growth and shrinking dynamics of the filaments likely contribute to these biological processes, it is useful to specifically understand how the activity of different myosin motors can account for the diversity and dynamics of actin-based structures observed in vivo [2].
Stochastic agent-based models that explicitly simulate individual filament and motor dynamics provide useful tools for probing the dynamics of actin and myosin structures. In [2], we studied actin organization by building on the MEDYAN platform [4], which accounts for complex chemical dynamics of motors, actin, and crosslinkers, a mechanical polymer model for actin filament growth and shrinkage, as well as mechanochemical coupling. MEDYAN uses a stochastic reaction-diffusion scheme and force fields that model actin as semi-flexible polymers [4].
Several myosin motors have been hypothesized to exert force on the actin cytoskeleton, and motor properties that may vary among them include the step size of the motor or the motor binding rate. In the MEDYAN model, the step size \(d_\mathrm{step}\) impacts the base walking rate of the motors: \(k^0_\mathrm{fil,walk}=\frac{d_\mathrm{step}}{d_\mathrm{total}} \frac{1-\rho}{\rho}k_{\mathrm{head,bind}}\), where \(\rho\) is the motor duty ratio, \(d_\mathrm{total}\) is the distance between binding sites on the model actin monomers, and \(k_\mathrm{head,bind}\) is the single motor head binding rate [4]. Varying this parameter across a \(3\)-\(36\)nm range that is appropriate for this family of proteins yields actin organizations as in Movie 1 and Figure 1a), which show actin networks that transition from homogeneous meshes to two clusters to one aster-like structure. This is because an increase in this parameter increases the base motor walking rate, so that myosin motors have better access to filaments and further contract the network. These patterns hold even across multiple stochastic simulations, as illustrated by the network and geometric measures in Figure 1b), which we have used to characterize the protein interactions through time [2]. Variations in other parameters, such as the motor head binding rate, lead to more complex changes given that this parameter affects protein interaction mechanisms in a nonlinear way [2].
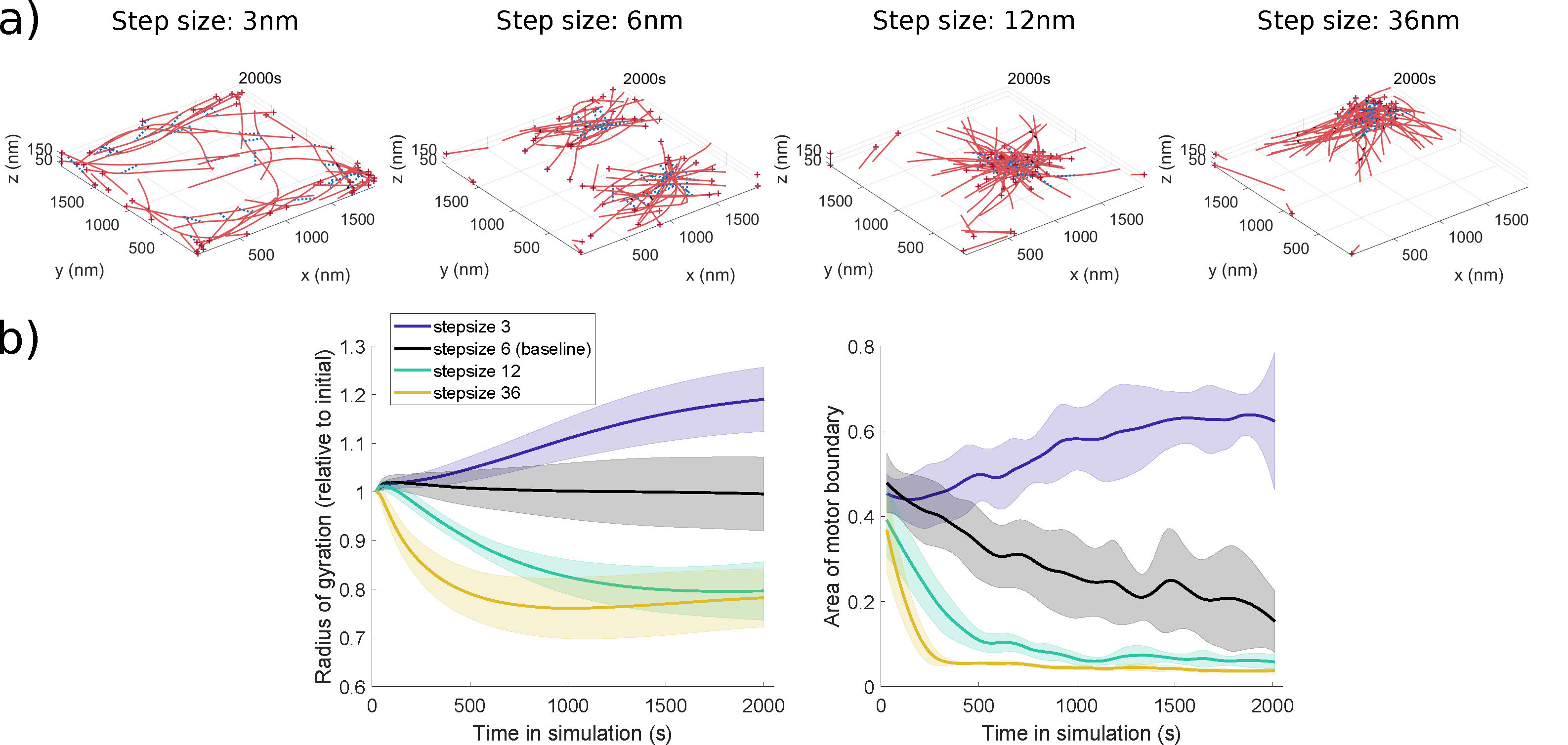
Figure 1: a) Final simulation snapshots at each indicated motor step size, showing aggregation of actin filaments for larger step sizes. b) The network radius of gyration decreases as motor step size is increased, reflecting the formation of actin clusters. The area of the polygon enclosing the myosin motor proteins decreases as motor step size increases, due to motor proteins binding to clustered actin filaments. Adapted from [2] under a CC-BY 4.0 license (https://creativecommons.org/licenses/by/4.0/).
Some experimental studies have shown that several types of myosin motors may regulate actomyosin organization [3]. Interestingly, [3] has also found some evidence of spatial segregation of the motors around the actin structures they generate. We therefore looked into the impact of two-motor populations with different kinetic parameters on the organization
of actin cytoskeletal networks in agent-based model simulations [2]. For motors with different step sizes, we found that the actomyosin organization is tuned in the sense that geometric measures of cytoskeletal network behavior lie in-between those corresponding to the behaviors of interactions with a single motor population (Figure 2a)). In other cases, one of the motors dominated the dynamics in terms of the emergent organization, and in few parameter regimes, we observed some motor segregation using geometric and spatial statistics measures (Figure 2b) and Movie 2). Overall, the approaches summarized here and further detailed in [2] illustrate rich network remodeling by the myosin motors, including the emergence of bundles, asters, and homogeneous distributions that have been previously observed in computational and experimental studies. Data and scrips are available at [1].
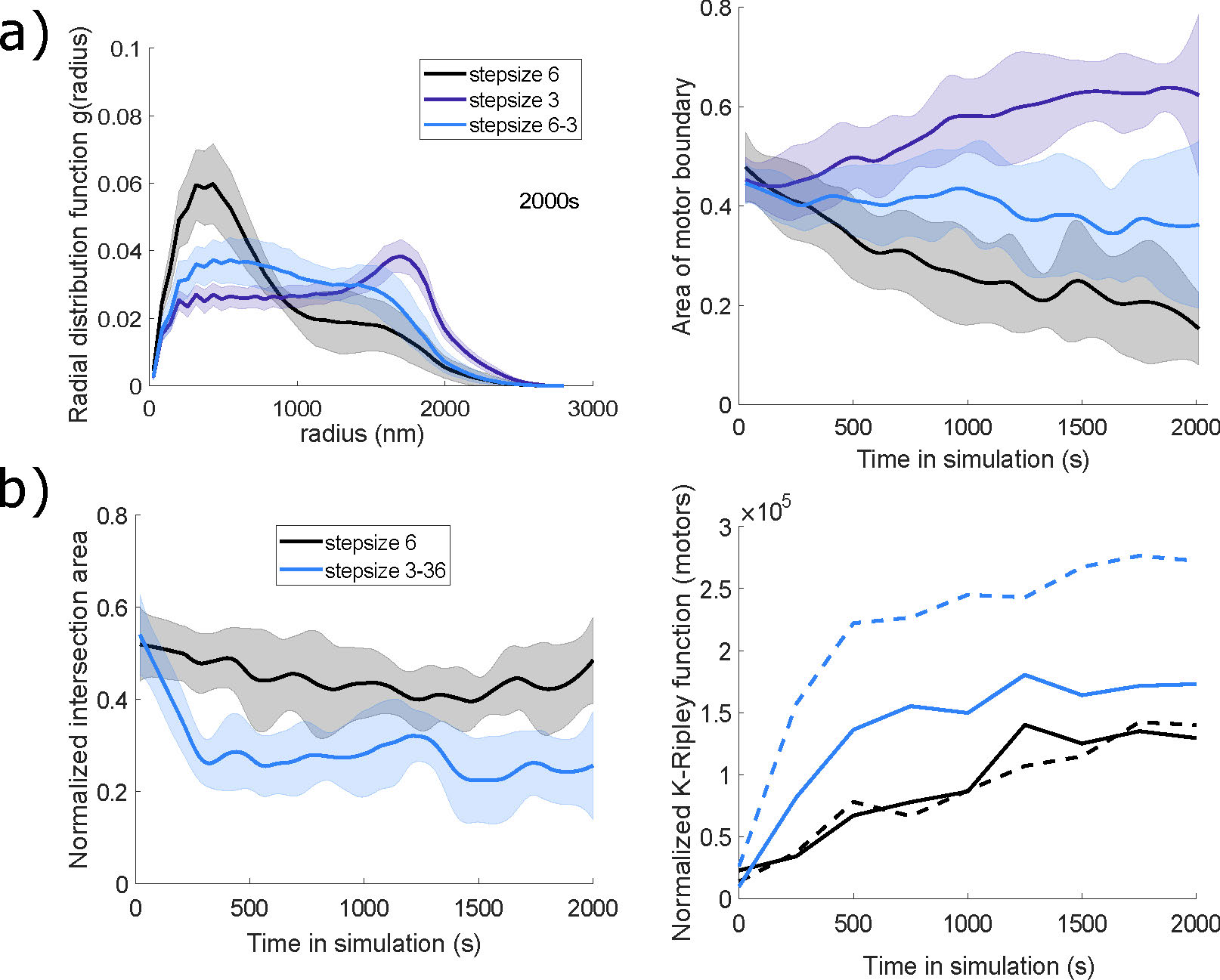
Figure 2: Evidence of tuning (a) and motor spatial segregation (b) in simulations with two motor populations with different step sizes (a): \(3\)nm and \(6\)nm; and b): \(3\)nm and \(36\)nm). a) Measures of radial
distribution and area of the polygon bounding all motor proteins fall between the values calculated for the motor proteins acting alone. b) The intersection area of the two motor protein populations (blue line) is lower compared to two identical motor populations with baseline parameters. The normalized K-Ripley function, measuring the spatial distribution of each motor population, shows that the large step size motor (blue solid line) has a tighter cluster distribution within the emergent actomyosin network than the small step size motor (blue dashed line). Adapted from [2] under a CC-BY 4.0 license (https://creativecommons.org/licenses/by/4.0/).
Movie 1. Evolution of the actin network with varying motor step sizes. Adapted from [2] under a CC-BY 4.0 license (https://creativecommons.org/licenses/by/4.0/).
Movie 2. Evolution of the actin network with two motor populations with different step sizes (blue: \(3\)nm, green: \(36\)nm).
References
[1] M.-V. Ciocanel, Data and scripts from: Actin reorganization
throughout the cell cycle mediated by motor proteins, https://doi.org/10.7924/r4zp43t43, 2021.
[2] M.-V. Ciocanel, A. Chandrasekaran, C. Mager, Q. Ni, G. A. Papoian, and A. Dawes, Simulated actin reorganization mediated by motor proteins, PLoS Computational Biology, 18 (2022), p. e1010026.
[3] V. C. Coffman, T. M. Kachur, D. B. Pilgrim, and A. T. Dawes, Antagonistic behaviors of NMY-1 and NMY-2 maintain ring channels in the C. elegans gonad, Biophysical Journal, 111 (2016), pp. 2202-2213.
[4] K. Popov, J. Komianos, and G. A. Papoian, MEDYAN: Mechanochemical simulations of contraction and polarity alignment in actomyosin networks, PLoS Computational Biology, 12 (2016), p. e1004877.
| Author Institutional Affiliation | Duke University |
| Author Email | |
| Keywords | Mathematical Biology, Biological Systems, Patterns and Simulations |