These pictures show results of an algorithm which covers an invariant manifold with small patches - found by integrating the first and second order terms in a Taylor series along trajectories (i.e., a fat trajectory).
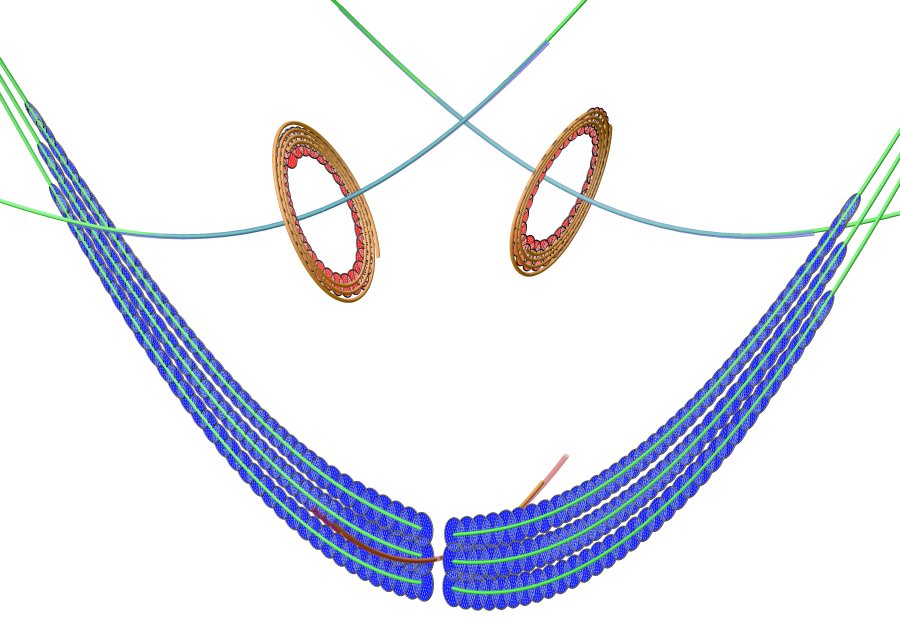
Fattened trajectories in the Lorenz System: Eight fattened trajectoriees are shown (six on the stable manifold of the origin, and one each on the unstable manifolds of the other two fixed points). Green tubes are trajectories backward in time, orange are forward in time.
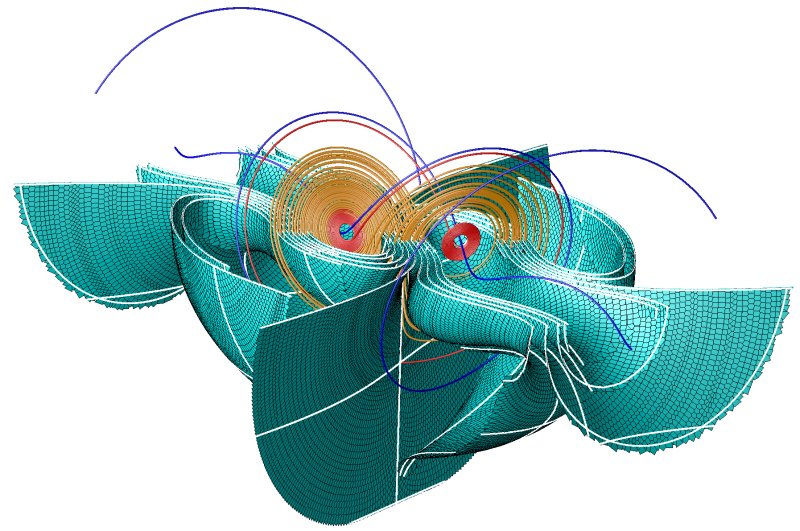
X-Y section of the Lorenz Manifold: This figure shows the X-Y section of the Lorenz manifold which contains the two fixed points that are not the origin, the part of the manifold below the section (cyan), the stable manifolds of the two fixed points (the blue curves), and a trajectory that lies near the chaotic attractor (the orange curve). The red trajectories start near each fixed point, and spiral outward near their unstable manifolds.

Stable manifold of the origin, shortish time: This shows a calculation of the stable manifold of the origin of the Lorenz system at the "standard" parameter values (s=10,r=28,b=8/3). It was computed using overlapping quadratic approximations to the manifold, found by integrating the terms in a Taylor series (up to second order) along trajectories.
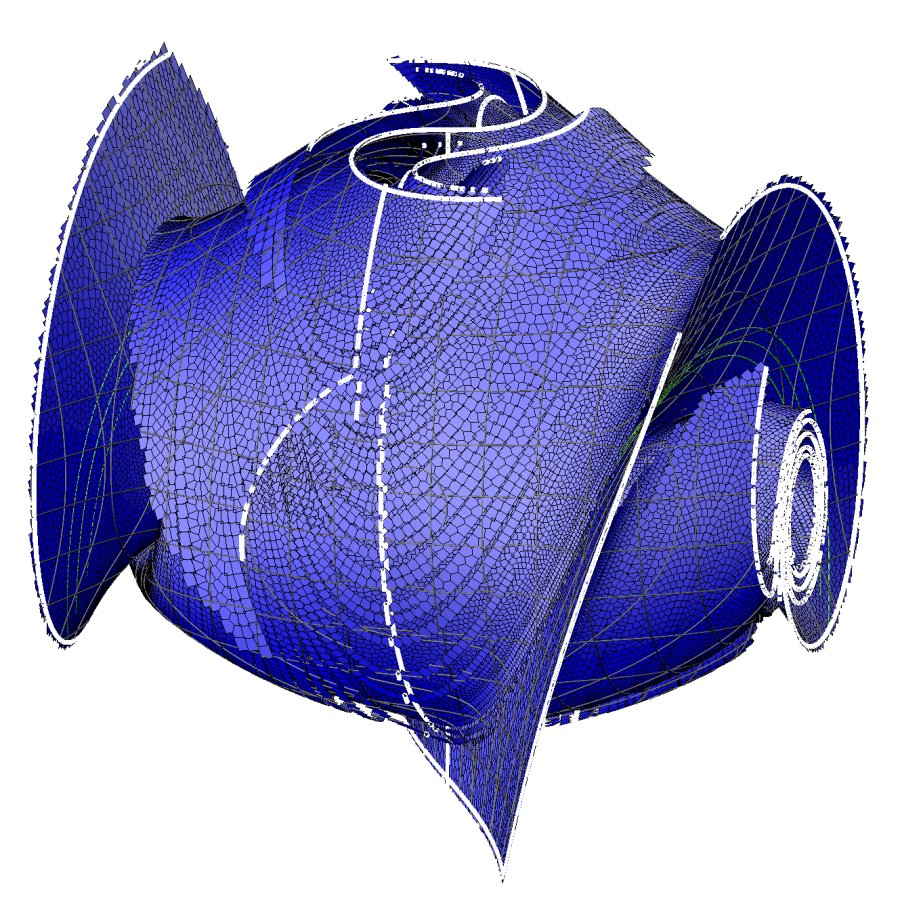
Stable manifold of the origin, longer time: This shows a calculation of the stable manifold of the origin of the Lorenz system at the "standard" parameter values (s=10,r=28,b=8/3). It was computed using overlapping quadratic approximations to the manifold, found by integrating the terms in a Taylor series (up to second order) along trajectories. I stopped this computation before the manifold was completely covered (I'm impatient). As a result you can see the fat trajectories. I thought it gave a better idea of the algorithm.
| Author Institutional Affiliation | IBM Research |
| Author Email | |
| Author Postal Mail | 33-215 P.O. Box 218 Yorktown Height, NY 10590 |