Search

Hopf Bifurcations in Evolutionary Dynamics

Bifurcation and Continuation

By Darren Pais, Carlos H. Caicedo-Nunez, Naomi E. Leonard
Print
The replicator-mutator equations from evolutionary dynamics serve as a model for the evolution of language, behavioral dynamics in social networks, and decision-making dynamics in networked multi-agent systems. Analysis of the stable equilibria of these dynamics has been a focus in the literature, where symmetry in fitness functions is typically assumed. We explore asymmetry in fitness and show that the replicator-mutator equations exhibit Hopf bifurcations and limit cycles for increasing mutation strength \(\mu\). The first animation shows phase portraits of the dynamics as a function of \(\mu\), illustrating a Hopf bifurcation for a particular choice of fitness matrix. The second animation shows bifurcation plots of the dynamics for a class of circulant fitness matrices.

We prove conditions for the existence of stable limit cycles arising from multiple distinct Hopf bifurcations of the dynamics in the case of circulant fitness matrices. In the noncirculant case, stable limit cycles of the dynamics are coupled to embedded directed cycles in the payoff graph as shown in the third plot in this submission. These cycles correspond to oscillations of grammar dominance in language evolution and to oscillations in behavioral preferences in social networks; for decision-making systems, these limit cycles correspond to sustained oscillations in decisions across the group.

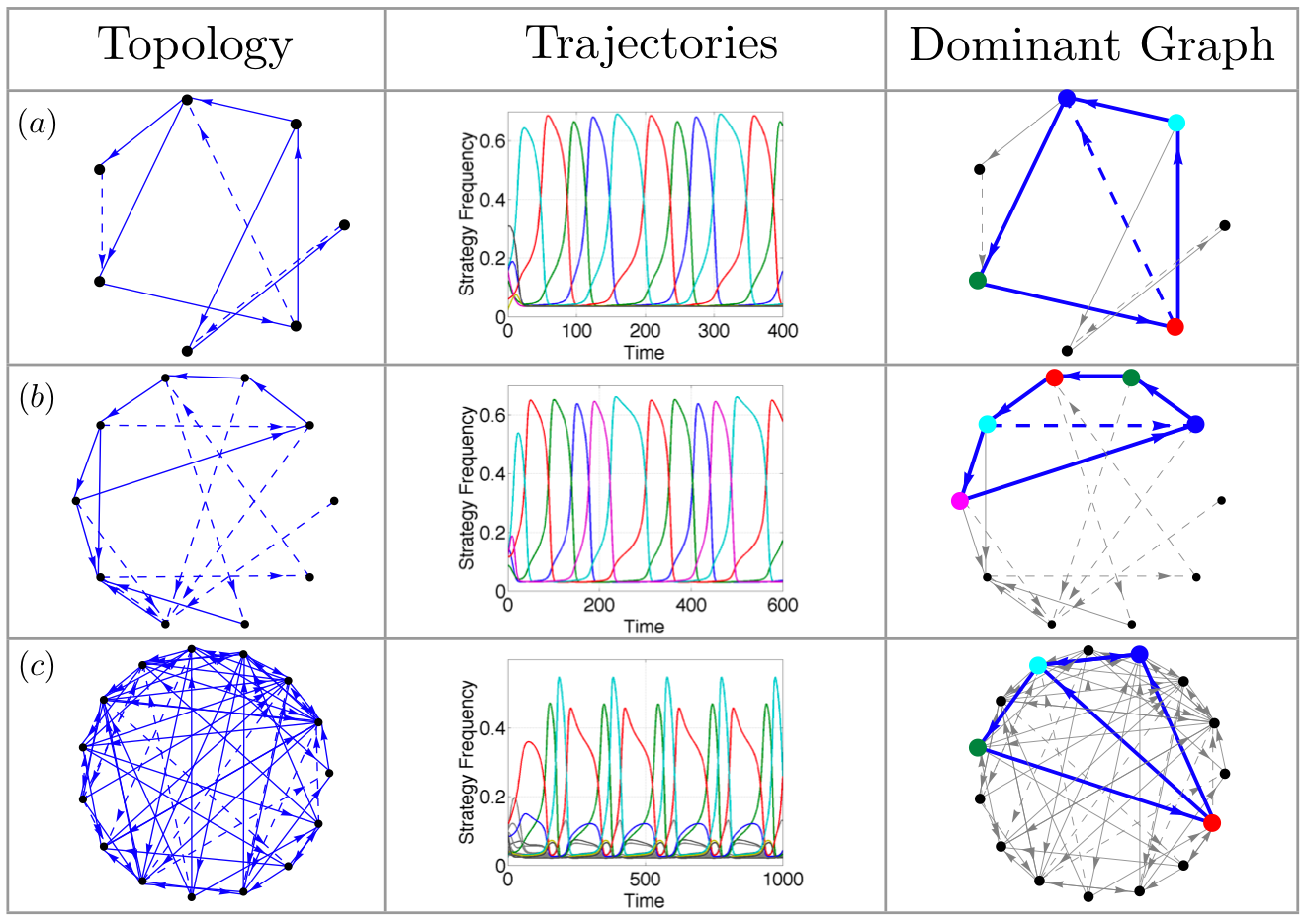
The left panel shows the payoff graph with two types of edges: strong edges (solid lines) with a weight of $b$ and weak edges (dashed lines) with a weight of \(\epsilon \017b\); here \(b = 0.7\) and \(\epsilon=0.1\). The center panel shows the resulting trajectories with mutation (Q2) and suitable \(\mu\)\026 (0.2 in (a), 0.25 in (b) and 0.27 in (c)). The right panel highlights the interconnection between nodes corresponding to the dominant components of the limit cycle trajectories. The color of each of the nodes on the payoff graph matches the color of the corresponding trajectory in the center panel. In each case, it is observed that there is a directed cycle between the dominant component nodes.
Author Institutional AffiliationPrinceton University
Author Email
Author Postal MailD-234 Engineering Quadrangle, Princeton University, Princeton, NJ 08544
Notes
For further details, please refer to:
Pais D, Caicedo-Nunez CH, Leonard NE. Hopf Bifurcations and Limit Cycles in Evolutionary Network Dynamics. SIAM J. Appl. Dyn. Sys. 11(4), 1754-1884, 2012.

Documents to download

  • Animation of phase portraits showing limit cycles(.mp4, 3.15 MB) - 3502 download(s) Animation of phase portrait, corresponding to Figure 3.5 in the main text, for the replicator-mutator dynamics with $N=3$ and directed cycle topology. The animation on the left shows, as a function of mutation strength $\\mu$, the nullclines (red, green and magenta), the vector field (grey arrows) and the equilibria (filled circles are stable, unfilled circles are unstable). The animation on the right shows, as a function of mutation strength $\\mu$, sample trajectories for randomly chosen initial conditions. The color scale indicates the magnitude of the flow (vector field) with hot colors corresponding to fast flow. A limit cycle appears for an intermediate range of values of $\\mu$.
  • Animation of bifurcation plots(.mp4, 1.81 MB) - 3509 download(s) Animation of bifurcation plots, corresponding to Figure 4.3 in the main text, as a function of payoff graph parameter $\beta$ for fixed parameter $\alpha$. The blue curves correspond to stable equilibria, red curves to unstable equilibria, and magenta curves to stable limit cycles. This slice of parameter space is illustrated in the top left of Figure 4.3; the Hopf bifurcation disappears at intersections of this slice with the red curves in the figure.

More links

Tags:

Please login or register to post comments.

Name:
Email:
Subject:
Message:
x