This work investigates the stability and dynamics of two dimensional patterns whose substructure is based on an underlying one dimensional localized state. The framework for our investigation is the variational Swift-Hohenberg equation
$$ u_t = ru - (1+ \Delta^2)^2\, u + \nu u^2 - u^3$$
which admits a large family of stable localized states whose profiles each feature exponentially decaying tails. Domains such as stripes and closed planar curves whose cross-sectional profiles are given by these one dimensional localized states can remain coherent in two dimensions and undergo sinuous motion. An analysis of this motion yields the geometric evolution law
$$
\rho_t = \gamma \kappa + \epsilon^2 ( \kappa_{ss} + \kappa^3 )
$$
for the normal motion of a curved domain with cross-section width \C\mathcal{O}(\epsilon)\). The parameter $\gamma$ is known in terms of certain integrals of the one dimensional localized state. This reveals a space filling mechanism when \(\gamma > 0\) based on ill-posed leading order dynamics with a higher order regularizing term. For \(\gamma < 0\), the curve shortens in length and equilibrates to radially symmetric states.

A simulation of the Swift-Hohenberg equation with \(r=-3.9\) and \(\nu = -4.7\) initialized with zero initial data except along a slightly elliptical curve. In the direction transverse to the curve, the solution quickly stabilizes to a one dimensional localized profile from which the value \(\gamma = -0.2335\) is calculated. The curvature driven dynamics, in conduction with repulsive forces between the curve and its distal segments, generates a space filling labyrinth.
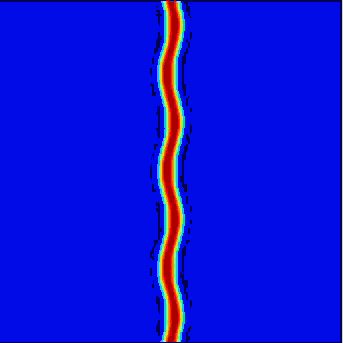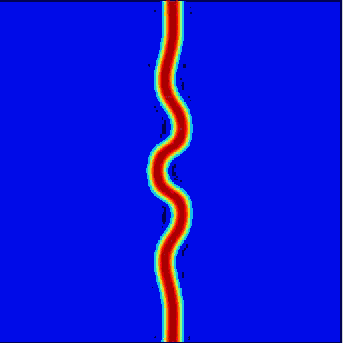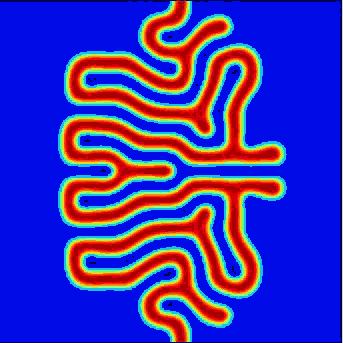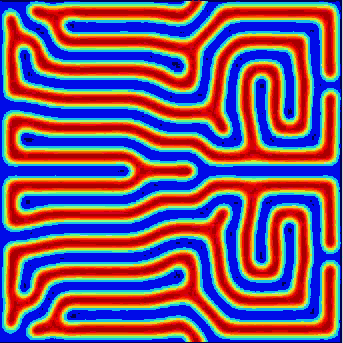
Instability of a stripe followed by space filling dynamics. Parameter values \(r=-3.9\) and \(\nu = 4.7\).
| Author Institutional Affiliation | University of Notre Dame and University of Arizona |
| Author Email | |
| Author Postal Mail | Applied Computational Math and Statistics, 153 Hurley Hall, University of Notre Dame, South Bend, IN, USA, 46617 |
| Notes | SIAM J. Appl. Dyn. Syst., (2013) 12(2), 650–673. |
| Keywords | Localized states, Surface diffusion, Geometric motion |