Shown are approximations to natural invariant measures ("SRB-measures") in the Lorenz system and in Chua's circuit.
The underlying computational technique consists of (1) computing a covering of the underlying invariant set via a multilevel-subdivision algorithm and (2) discretization of the corresponding transfer-operator (Perron-Frobenius operator) using a Galerkin-approach. An invariant vector of the discretized operator yields an approximate invariant measure.

Natural invariant measure in Chua's circuit for the parameter values \(\alpha=18\), \(\beta=33\), \(m_0=-0.2\) and \(m_1=0.01\).
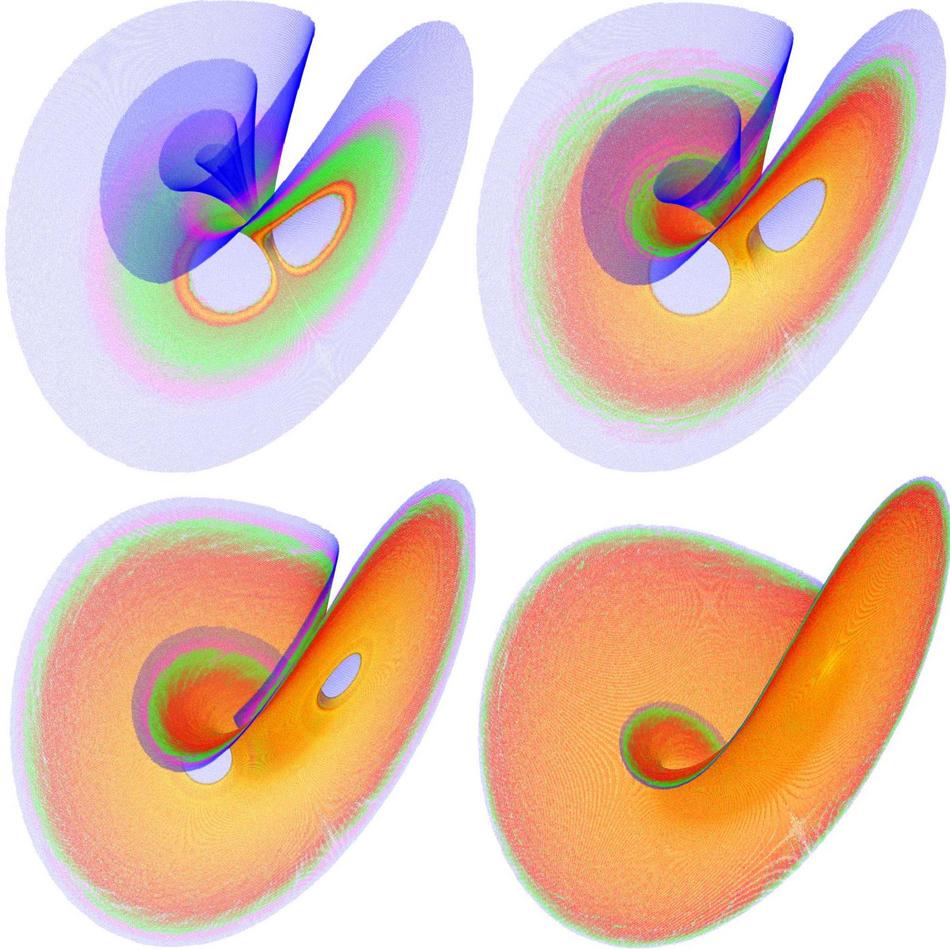
Natural invariant measures in the Lorenz system for the parameter values \(\beta = 0.4, 0.8, 1.2\) and \(8/3\) (from left to right, top to bottom). The other parameter values were fixed to \(\sigma = 10\) and \(\rho = 28\).
| Author Institutional Affiliation | University of Paderborn, Germany |
| Author Email | |
| Author Postal Mail | Institute for Mathematics, University of Paderborn, Warburger Str. 100, 33098 Paderborn, Germany |
| Notes | The pictures have been rendered in collaboration with Martin Rumpf ( [email protected]) using the software platform GRAPE. |
| Keywords | natural invariant measure, SRB-measure, transfer operator, set oriented method |