Typically, at the moment of a homoclinic bifurcation, the two-dimensional stable manifold of the saddle equilibrium, when followed along the homoclinic orbit, may form either an orientable or nonorientable surface, and one speaks of an orientable or a nonorientable homoclinic bifurcation.
A change of orientability occurs at two kinds of codimension-two homoclinic bifurcations, namely, an inclination flip and an orbit flip. The stable manifold of the saddle point is neither orientable nor nonorientable at either of these bifurcations. In these animations, we illustrate how the stable manifold of the saddle organizes the phase space globally near these homoclinic bifurcations in a model by Bjorn Sandstede.
Material taken from:
P Aguirre, B Krauskopf & H M Osinga, "Global invariant manifolds near homoclinic orbits to a real saddle: (non)orientability and flip bifurcation," SIAM J. Appl. Dyn. Syst., 12 (2013), pp. 1803-1846.
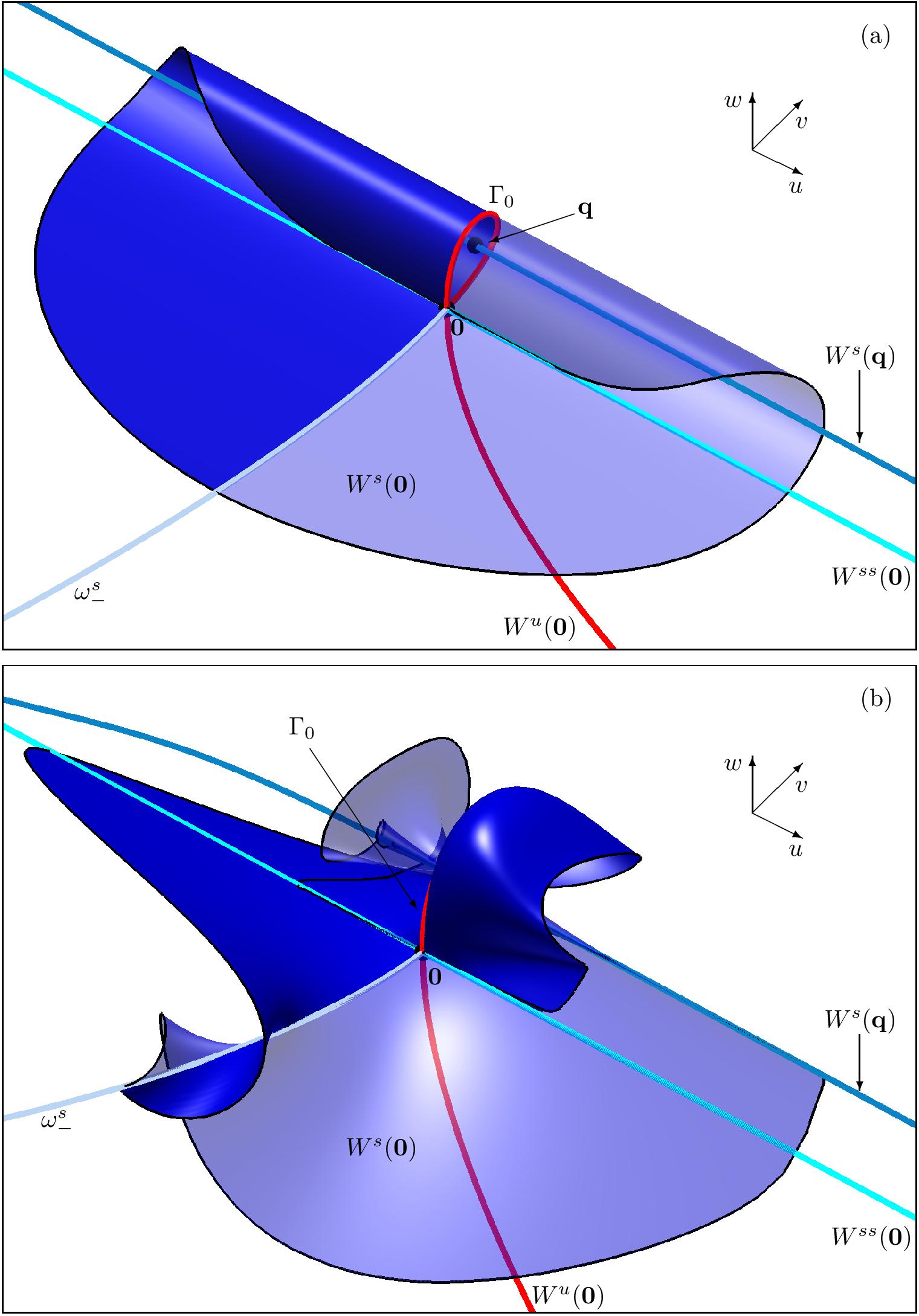
The stable manifold of a saddle equilibrium is either an orientable or nonorientable surface at a codimension-one homoclinic bifurcation.
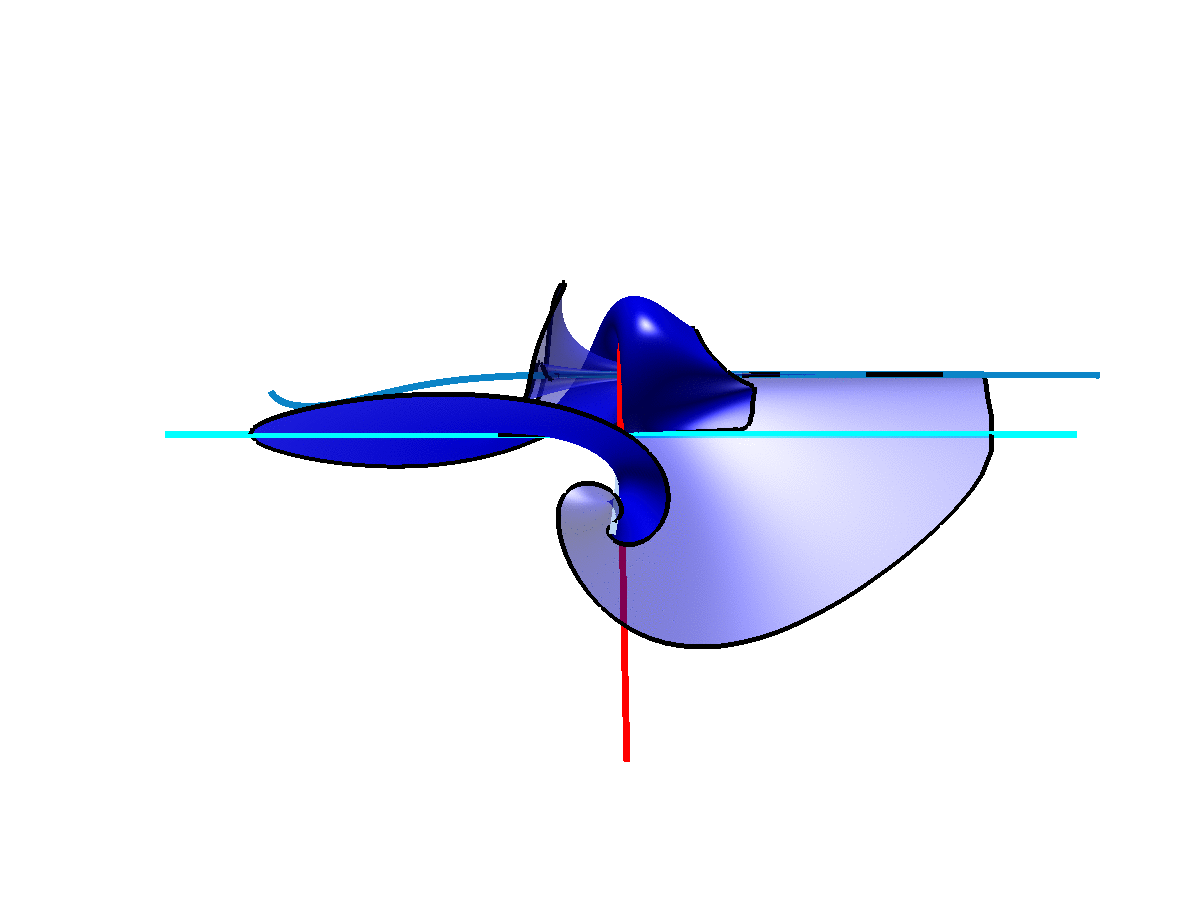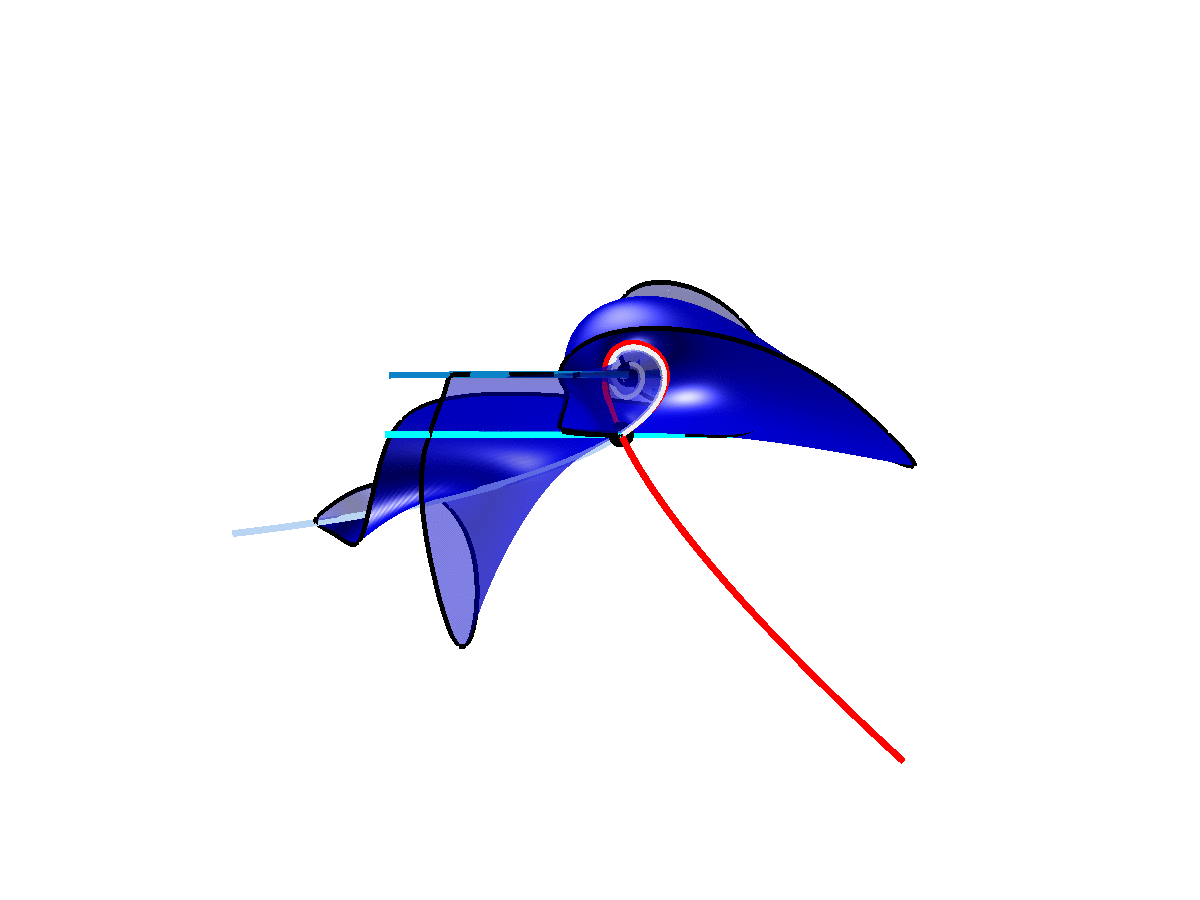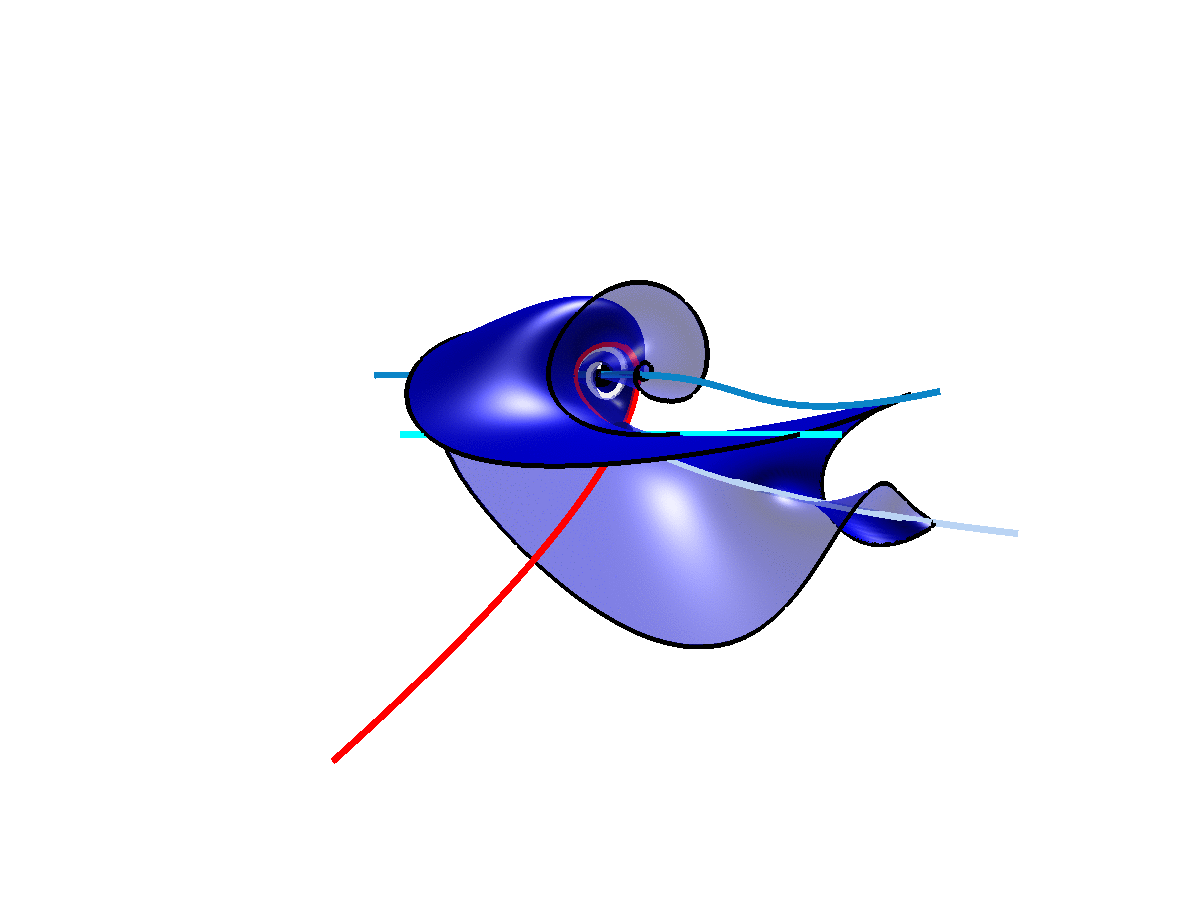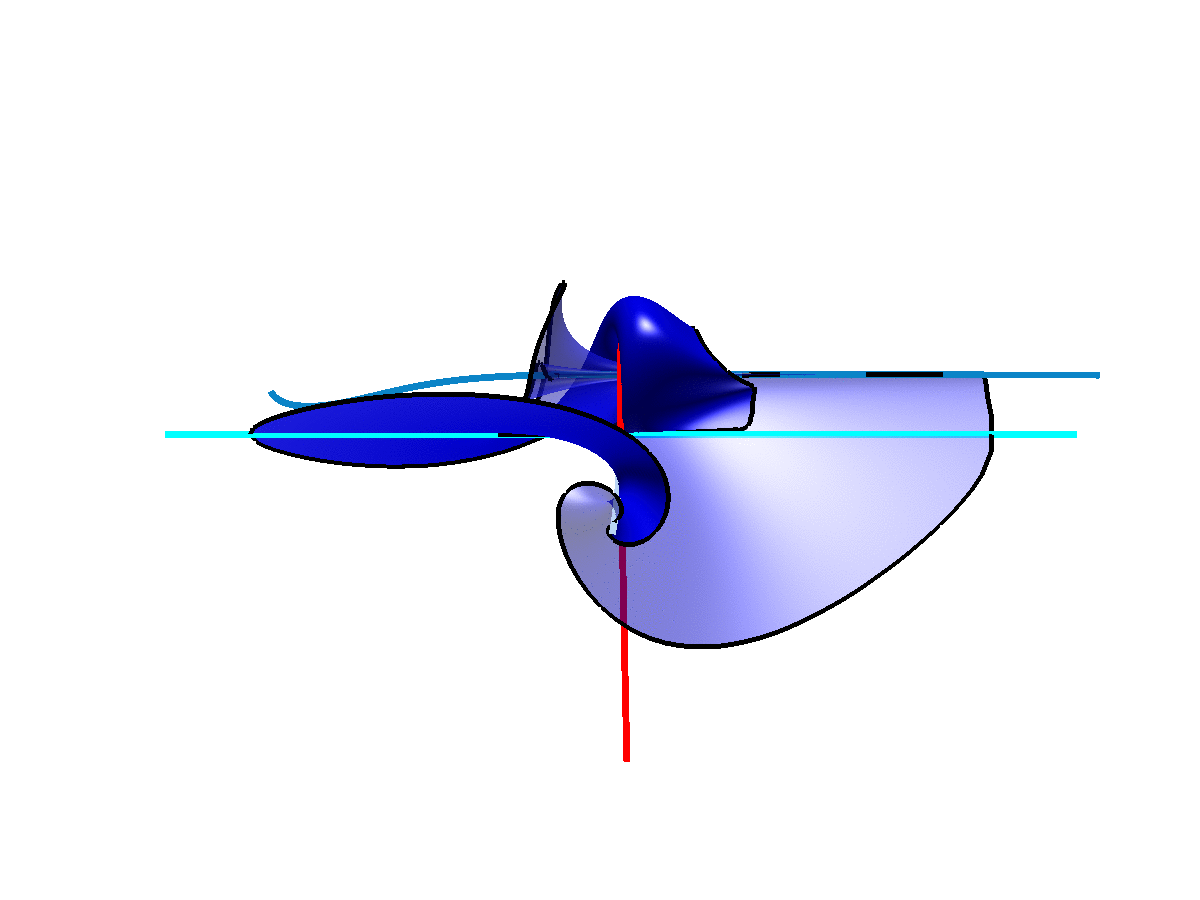
The two-dimensional stable manifold of a saddle equilibrium at a codimension-one non-orientable homoclinic bifurcation. The solid half of the surface comes back onto the transparent half, and vice versa, to form a topological Möbius strip.

At a codimension-two inclination flip homoclinic bifurcation, the stable manifold of the saddle comes back along the weak stable direction, which violates a genericity condition for a homoclinic connection. In doing so, the manifold is neither a topological cylinder nor a topological Möbius strip.

At a codimension-two orbit flip homoclinic bifurcation, the homoclinic orbit converges to the equilibrium along the one-dimensional strong stable manifold. This causes the two-dimensional stable manifold of the saddle to turn from an orientable surface into a nonorientable surface, or vice versa.
| Author Institutional Affiliation | Departamento de Matemática, Universidad Técnica Federico Santa María, Chile |
| Author Email | |
| Notes | This is a joint work with Bernd Krauskopf and Hinke Osinga, The University of Auckland. |
| Keywords | Homoclinic bifurcations, global invariant manifolds, inclination flip, orbit flip |