We summarise an article published by Nick McCullen and Thomas Wagenknecht in Scientific Reports [1]. This work presents results on networks of interacting species, in particular on pattern formation in this context, which is relevant to many applications in complex systems. The transition from states where one or a few nodes only are active and full-scale Turing patterns is shown to occur through a snaking scenario, which can be computed using numerical continuation. Consecutive branches of the snaking diagram, separated by fold bifurcation points, correspond to states with more and more differentiated nodes.

The starting point is the following template of classical reaction diffusion PDEs:

\begin{equation} \label{e:pde}
\begin{split} 
\partial_t u & =  f(u, v) + \varepsilon \nabla^2 u,\\
\partial_t v & =  g(u, v) + \varepsilon \nabla^2 v,
\end{split} \end{equation}

where \(u\) and \(v\) are activator and inhibitor chemical species. The authors focus on the Mimura-Murray prey-predator (activator-inhibitor) network model,  

\begin{equation}
f(u,v) = \frac{au+bu^2-u^3}{c} - uv, \quad g(u,v) = uv-v -dv^2,\label{eqn:mimu}
\end{equation}

and pose the problem on a network:

\begin{equation} \label{e:rdco}
\begin{split} 
\dot{\bf u} & =  f({\bf u}, {\bf v}) + \varepsilon L {\bf u},\\
\dot{\bf v} & =  g({\bf u}, {\bf v}) + \sigma \varepsilon  L {\bf v},
\end{split} \end{equation}

where \(L\) is the discrete Laplacian matrix: \(L_{ij}\) is \(1\) (resp. \(0\)) if two distinct nodes \(i\) and \(j\) are connected (resp. not connected), and the diagonal term is \(L_{ii}=-k_i\), where \(k_i\) is the degree at node \(i\) (hence each row sums to zero). In the article, the following parameter values were chosen: \(a=35\), \(b=16\), \(c=9\), \(d=2/5\), \(\varepsilon=0.12\). For these parameter values the system possesses a homogeneous equilibrium where all nodes have values \((\bar{u}, \bar{v})=(5,10)\). This homogeneous state is stable for small values of \(\sigma\), but its stability is lost through a subcritical bifurcation at \(\sigma \approx 15.5\).

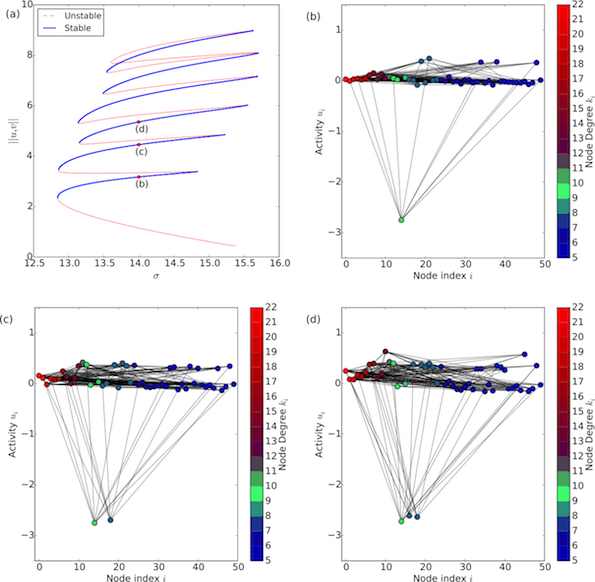
The growth of small-scale patterns of activity of nodes. (a) A bifurcation diagram showing the solution-space connecting patterns of increasing numbers of differentiated nodes. The control parameter \(\sigma\) is plotted against the magnitude of the activation vector of the two species. Thick (blue) and thin (red) lines show stable and unstable solutions, respectively. The first three solutions are shown in  (b)-(d), with nodes ordered left-right by decreasing node degree (\(d_k\) network neighbours, also shown in colour) and the lines show the links between adjacent nodes. An animation showing the bifurcation diagram and the corresponding stable and unstable patterns can be downloaded following this link.

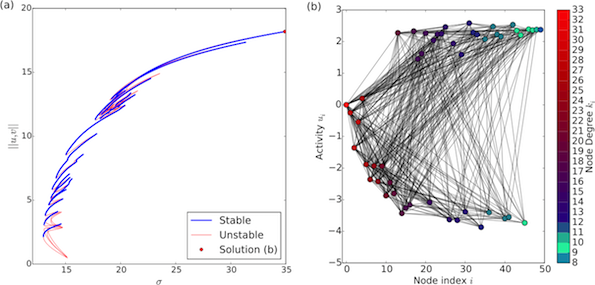
Growth from localised activity to system-scale Turing-type patterns in a network with attachment degree \(M=10\).  (a) The snaking bifurcation diagram, with solutions at turning points numbered and (b) a bulk-mode pattern on the network nodes. The optimal degree \(d_k^*=9\) nodes (shown in green) are towards the periphery of the network.

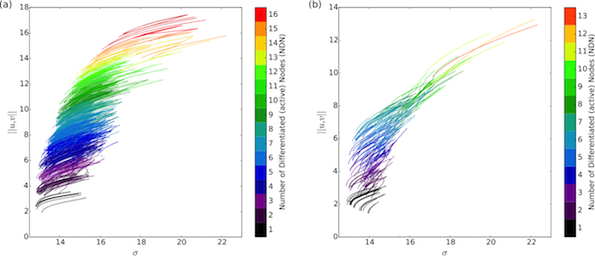
Full set of solution branches at lower \(\sigma\) values, showing both stable and unstable branches together. Colours indicate the number of differentiated nodes on each curve. (a) The \(M=5\) networks with \(d_k^*\) intermediate in position, and (b) the \(M=10\) network with \(d_k^*\) near the periphery.

Statistical distributions of solutions, shown as the both histogram and 2D density plot over the bifurcation space for a range of values of the control parameter \(\sigma\). (a) & (b) are for the \(M=5\) case where the small-scale patterns do not directly connect to the system-scale patterns and (c) & (d) for the \(M=10\) case where they do connect. In both cases two peaks can be seen, one for the snaking column and the other for the bulk solutions.