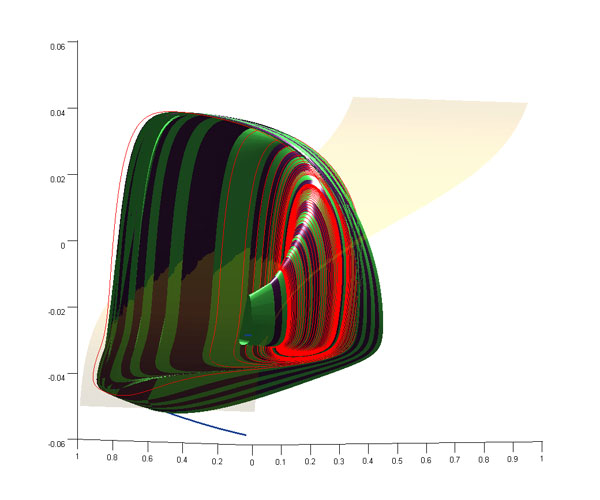
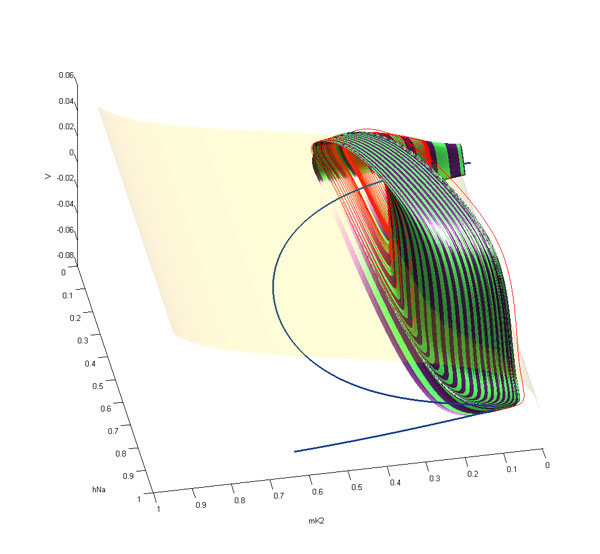
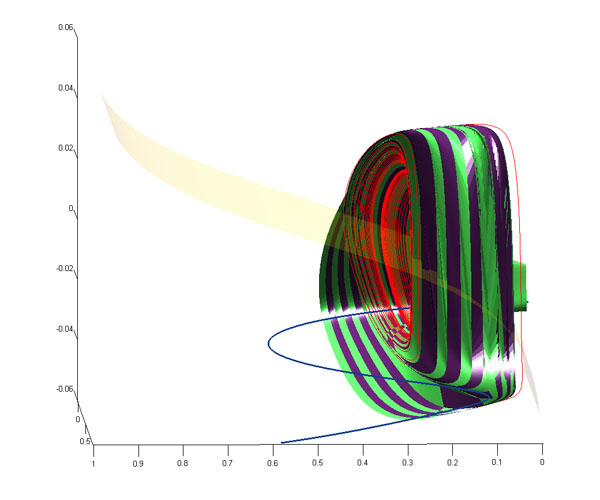
Three views on the parameterized slow motion manifolds and the 2D nullcline in a 3D leech inter-heart neuron model. The blue curve consists of equilibria of the system. The zebra-like surface with two folds is comprised of the periodic orbits. It ends up at the homoclinic saddle-node bifurcation (SNIC in modern jargon). Shown in red are the co-existent bursting and tonic-spiking orbits.
References:
- Shilnikov, A. L. and Cymbaluyk, G. Transition between tonic-spiking and bursting in a neuron model via the blue-sky catastrophe, Phys Review Letters, 94, 048101, 2005
- Cymbaluyk, G. and Shilnikov, A. L. Co-existent tonic spiking modes in a leech neuron model, J. Computational Neuroscience 18 (3), 255-263, 2005
- Shilnikov, A. L., Calabrese R. and Cymbalyuk, G. Mechanism of bi-stability: tonic spiking and bursting in a neuron model, Phys Review E 71(5), 056214-046221, 2005.
22
6
16
| Author Institutional Affiliation | Georgia State University |
| Author Email | |
| Author Postal Mail | Department of Mathematics & Statistics Georgia State University 30 Pryor Street, Atlanta, GA 30303 tel. 404.651.06.55 |
| Keywords | bifurcations, slow-fast systems, neuron models |