The Computational Continuation Core (COCO) is a Matlab-based software platform for numerical continuation of constrained solutions to nonlinear equations, e.g., those arising from discretization of finite- and infinite-dimensional boundary-value problems. COCO aims to provide a platform for advanced toolbox and atlas algorithm development, but also to enable all the functionality of existing continuation packages in a user-accessible format.
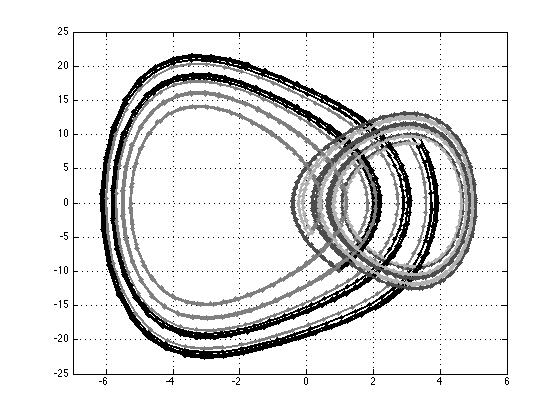
Periodic orbit in a nonlinear oscillator with piecewise constant forcing.
The basic philosophy of COCO, its command-line interface, and the detailed development of template toolboxes and atlas algorithms, as well as explicit code examples, are documented in the book Recipes for Continuation, published by SIAM in 2013. This includes discussion of the object-oriented problem construction paradigm of COCO, the handling of constraints and detection of special points during continuation, the design of multi-dimensional atlas algorithms, and support for adaptive discretization, including moving and comoving meshes.
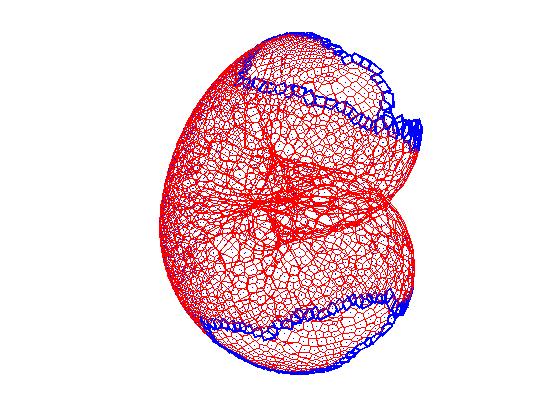
A three-dimensional embedding of the Klein surface.
The official COCO release, available at http://sourceforge.net/projects/cocotools, contains all the code printed in the book, including toolboxes and demos, but also code used to generate most of the figures in the book. The code is extensively commented and documented, and is further accompanied by help files that may be read and navigated using the Matlab help browser. To explore this content, after installation, type the command “doc recipes” on the command line.
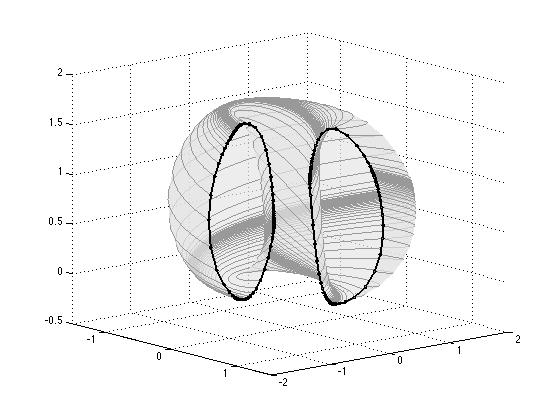
A quasiperiodic invariant torus.
The release also includes a short reference guide for command-line use of COCO, including the calling syntax and use of core commands. Additional documentation is available here in a suite of video tutorials illustrating the core principles of continuation and their implementation in COCO. The video files are also accompanied by a complete transcript.
The development of COCO is ongoing, with current emphasis on tools for bifurcation analysis of steady-state dynamics. Recent developments include:
- An equilibrium point toolbox, accompanied by a tutorial with six fully documented examples, including bifurcation analysis of equilibria, continuation of isola curves, and continuation of approximate eigenfunctions of a discretized Laplacian. The source code is also documented for developers.
- An experimental multi-dimensional atlas algorithm for algebraic problems that includes full step-size adaptivity and is accompanied by several partially commented examples of continuation of one- and two-dimensional manifolds, including continuation within computational domain boundaries and large variations in curvature.
Coming releases (the next is planned for Spring 2015), will include:
- An adaptive collocation toolbox for continuation of trajectory segments of finite-dimensional dynamical systems, accompanied by tutorial examples that illustrate continuation of of multi-segment boundary-value problems, e.g., heteroclinic orbits between equilibria and periodic orbits.
- An adaptive periodic orbit toolbox for smooth dynamical systems, with support for location and continuation of saddle-node, period-doubling, and torus bifurcations, as well as branch-switching at branch points and period-doubling points.
- An adaptive periodic orbit toolbox for hybrid (e.g., piecewise-smooth) dynamical systems, with support for location and continuation of saddle-node, period-doubling, and torus bifurcations, as well as branch-switching at branch points and period-doubling points.
- An updated version of the multi-dimensional atlas algorithm for adaptively discretized boundary-value problems.
| Keywords | Bifurcation analysis, Continuation |
| Model | |
| Software Type | |
| Language | |
| Platform | |
| Availability | |
| Contact Person | |
| References to Papers | |