
I am Dana, a second year PhD student of Mathematics at the University of Auckland, supervised by Hinke M. Osinga and Bernd Krauskopf. I graduated from the Mathematical Engineering program at Universidad Técnica Federico Santa María in Chile, supervised by Pablo Aguirre.
My interest in dynamical systems dates back to my second year of undergrad, in which I had the fortune to attend an ODE course with a strong focus on dynamical system’s qualitative theory. My surprise was even greater when we studied the beautiful visualisations of Lorenz's strange attractor and chaos. I immediately knew I wanted to know more about these topics. I approached Pablo Aguirre, who taught the course, and asked him if I could work on a project with him. He luckily accepted! As a result of this work, we published two papers. In the first one we describe the Allee thresholds and basins of attraction in a predation model with double Allee effect. We determined the complete bifurcation diagram and behaviour in the short and long term by using qualitative theory and the theory of bifurcation. In the second paper we study strategies to control the spread of dengue fever with the theory of dynamical systems. We proposed a (then) new method to calculate and visualise 3D invariant manifolds embedded in a 4D state space. This publication was additionally highlighted as free access in the Epidemiology Collection of SIAM.
Doing research during my undergrad opened a world for me, where I understood that visualisation and numerical methods — two worlds that fascinate me — enhance each other. I wanted to pursue that beautiful area of mathematics and I wished to be able to contribute my bit in the future. It is for this reason that I sought a PhD opportunity at the University of Auckland and to be part of the dynamical systems group there, well known for their contributions to theory, visualisation, and computational methods for dynamical systems. Upon arriving in New Zealand, the group welcomed me with open arms, helping me to overcome the language barrier. Here I have forged great bonds of friendship and team spirit. Every Friday the group get together and we discuss our projects, exchange ideas, and very enriching collaborations and discussions arise.
My research: blenders and wild chaos
In my PhD research, I am investigating when the chaotic behaviour of a dynamical system is robust, and how one can detect, quantify, and visualise this robustness. Higher-dimensional dynamical systems can exhibit a new and more complicated type of robust chaos, called wild chaos, that in many aspects is still unknown [1]. One of the difficulties is that, thus far, there are not many concrete examples or visualisation of wild chaos.
I want to find novel methods to illustrate the geometry behind wild chaos. Moreover, I am extending a visualisation technique to determine if a system exhibits this type of chaotic behaviour. One of the key elements to describe wild chaos are the (un)stable manifolds of fixed points and heterodimensional cycles. A heterodimensional cycle is formed by two intersection sets of different dimensions between stable and unstable manifolds. If one or more of these intersections are non-transverse, the heterodimensional cycle is generally thought not to be robust. However, for systems that exhibit wild chaos, non-transverse heterodimensional cycles exist in open intervals in parameter space. In other words, it must be possible to create non-transverse heterodimensional cycles for a wide range of parameters, and thus, robust chaos [2].
To construct such robust non-transverse intersection sets, Bonatti and Díaz introduced the notion of a blender: a blender admits invariant manifolds that behave as geometric objects of higher dimension than expected from the dimensions of the manifolds themselves [3]. In a three-dimensional system, a curve would give the impression that it is a surface. The first explicit and visualised example of a blender was presented by Hittmeyer, Krauskopf, Osinga and Shinohara in [4]. They define the carpet property as a method to check whether a manifold is a blender, and employ advanced numerical methods for the computation of stable or unstable manifolds to detect and illustrate their higher-than-expected dimensionality directly. The carpet property is a numerical test for denseness in projection, which is based on computing increasingly longer pieces of a one-dimensional global manifold: the manifold ‘‘looks’’ like a two-dimensional surface when viewed from an open set of appropriate directions.
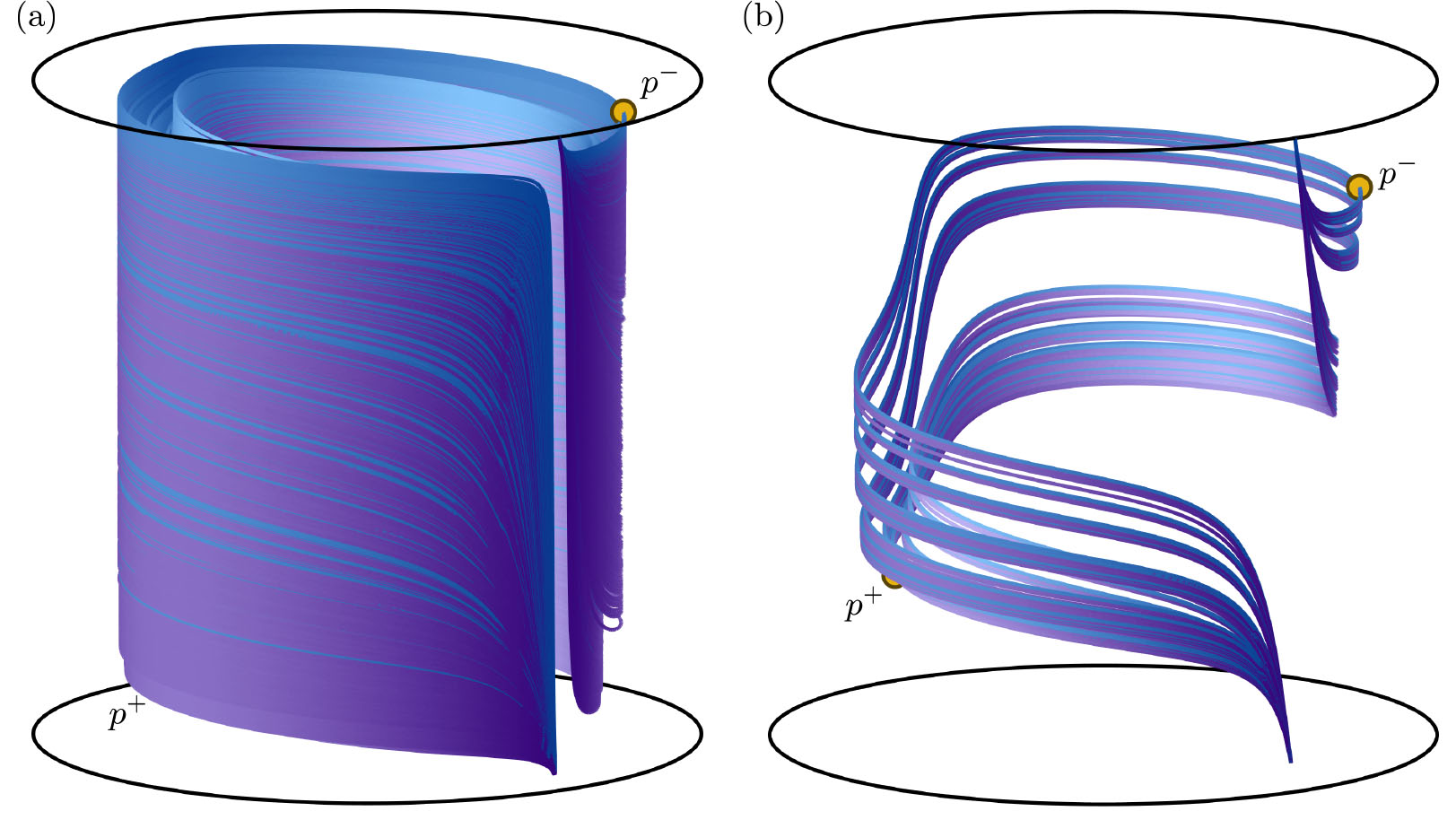
Figure 1: The stable manifolds of fixed points \(p^-\) (blue) and \(p^+\) (purple) of the Hénon-like family form a blender in panel (a). For a different value of a key parameter, on the other hand, they do not, as is shown in panel (b).
So far, I have extended the example in [4] to a family of orientable three-dimensional Hénon-like maps. Additionally, I have improved the advanced numerical techniques for the computation of one-dimensional stable and unstable manifolds in maps. Figure 1 shows the one-dimensional stable manifolds of two fixed points (\(p^+\) and \(p^-\)) in blue and purple, respectively. In panel (a) both manifolds are very intermingled and, moreover, are seen to behave as surfaces that accumulate on each other. Hence, the map has the carpet property and we conclude that we are looking at a blender. Panel (b) shows the same one-dimensional stable manifolds for a different value of the key parameter (which controls the central expansion). While the two manifolds are still intermingled, in contrast to panel (a), there are now clear gaps in the structure of the manifolds. This is evidence that the carpet property is lost, meaning that the blender disappears at a parameter value in between those for the two cases shown in Figure 1.
At present, I am developing different and complementary visualisation methods to understand how the orientability of the manifolds controls the mechanism behind losing the carpet property. This involves a geometric analysis of how two Cantor sets can be multiplied together and form a set that is no longer a Cantor set. Similar investigations will then be performed for other example systems to enhance our understanding of how wild chaos may arise, and what its geometric properties are. In the longer term, I plan to investigate whether these visualisation tools can be applied to observable data measured from experiments. This research will show whether high-dimensional forms of chaos matter in applications, for example, whether it can be of benefit to high-security encryption or desynchronisation strategies in epilepsy treatments.
I thank Pablo, who taught me the passion for dynamic systems and who has been a great support in pursuing my dreams. I also thank Hinke and Bernd for not only their support and invaluable guidance in my research, but also for being great role models as scientists and mentors.
References
[1] Bonatti and L.J. Díaz, Robust heterodimensional cycles and generic Dynamics, Journal of the Institute of Mathematics of Jussieu, 7 (3) (2008), pp. 469-525.
[2] C. Bonatti, S. Crovisier, L.J. Díaz, and A. Wilkinson, What is... a blender, Notices of the American Mathematical Society, 36 (10) (2016), pp. 1175-1178.
[3] C. Bonatti and L.J Díaz, Persistent nonhyperbolic transitive diffeomorphisms, Annals of Mathematics, 143 (2) (1996), pp. 357-396.
[4] S. Hittmeyer, B. Krauskopf, H.M. Osinga, and K. Shinohara, Existence of blenders in a Hénon-like family: geometric insights from invariant manifold computations, Nonlinearity, 31 (10) (2018), pp. R239-R267.