Bula! My name is Morgan, a PhD student studying applied mathematics at The University of Auckland in New Zealand. I did my undergraduate degree in engineering, specializing in engineering science, conjoint with science, majoring in mathematics. For the summer after finishing my undergraduate degree, I had the chance to do a summer research project within the Faculty of Science looking at the dynamics of a conceptual climate model. I really enjoyed this, so I continued looking at climate models during my Masters, looking at the dynamics of an extended energy balance model. The multiple timescale dynamics theory behind the model I was looking at fascinated me, so when I had the chance to do my PhD in multiple timescale dynamics, I went for it.

I am currently in my third year of my PhD under the supervision of Vivien Kirk and Claire Postlethwaite. We are working with Mathieu Desroches analysing a new type of bifurcation that is seen in some multiple timescale systems. It has been observed that in some systems [1, 2], the onset of bursting and spike-adding transitions is associated with a so-called folded homoclinic bifurcation. This bifurcation has not been systematically studied. Our research focuses on the nature and origins of the complex oscillations that arise from this bifurcation.

The overall aim for this PhD project is to understand the role a folded homoclinic bifurcation has on spike-adding and provide a systematic study of this bifurcation. We use dynamical systems theory to study the generic unfolding of a folded homoclinic bifurcation. In addition, I will investigate how this generic behavior is manifested in specific systems, depending on the details of the global features and geometry of them.

Systems with multiple timescales frequently have the property that one or more variables in the system evolve on a much faster timescale than other variables. Solutions to models of multiple timescale systems may exhibit bursting, which occurs when intervals of rapid spiking of the amplitude of one or more variables are interspersed with quiescent periods during which the amplitude changes slowly. There has been a great deal of interest over many years in the mathematical mechanisms underlying bursting, particularly the mechanisms that are associated with a change in the number of spikes in a bursting solution.

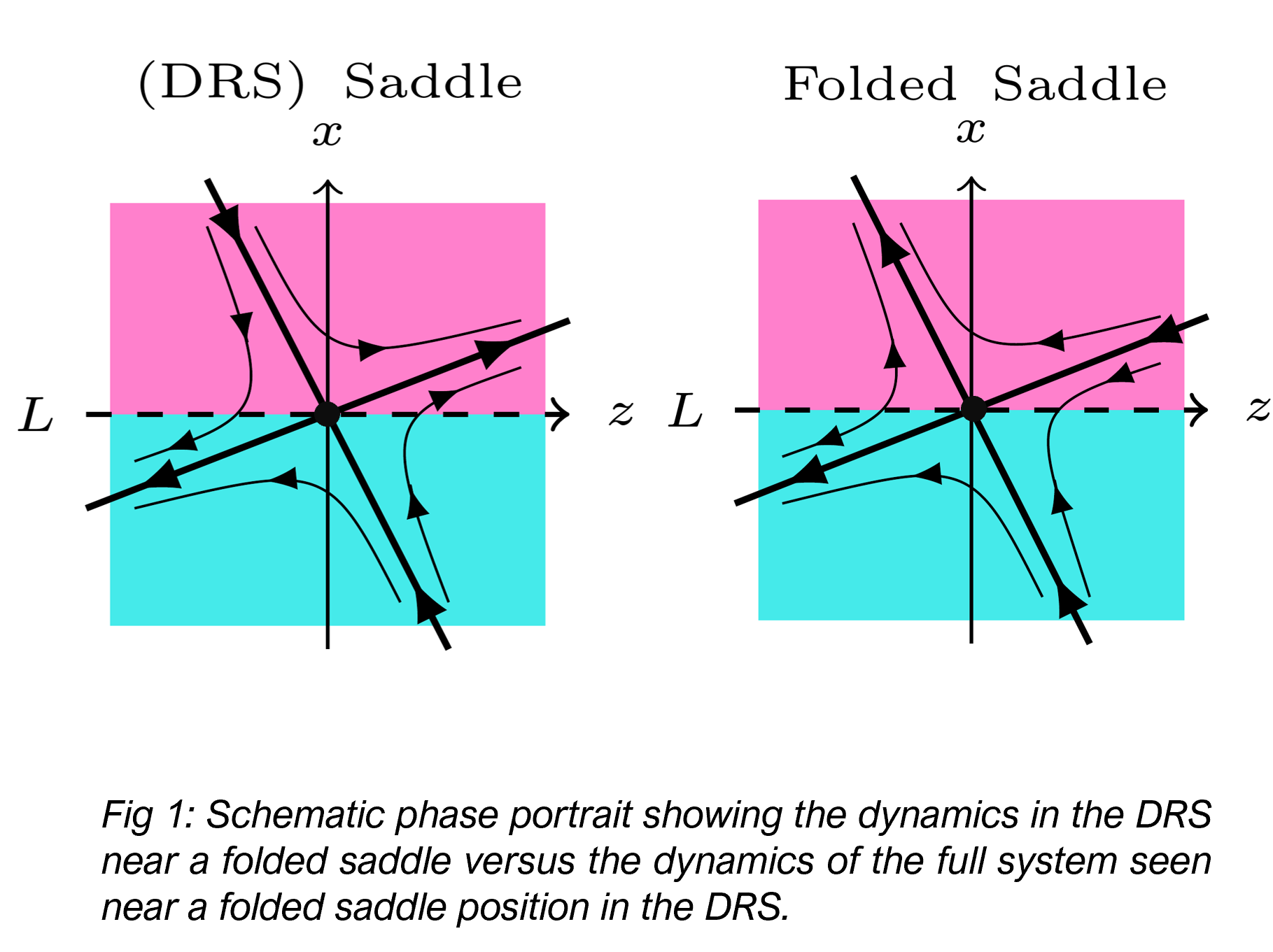
The types of systems in which folded homoclinic bifurcations may arise are those with at least two timescales and with at least two variables that evolve on slower timescales than the fastest variable. These systems have a so called desingularised reduced system (DRS) of dimension at least two; we can use this reduced system to understand the dynamics in the full system. In some cases, the desingularised reduced system may also have extra equilibrium points that the full system does not. These occur along fold lines and are categorized based on the equilibrium in the DRS. I am interested in systems that have what is called a folded saddle. This is an extra equilibrium on the fold line appearing as a regular saddle in the DRS (Fig. 1).

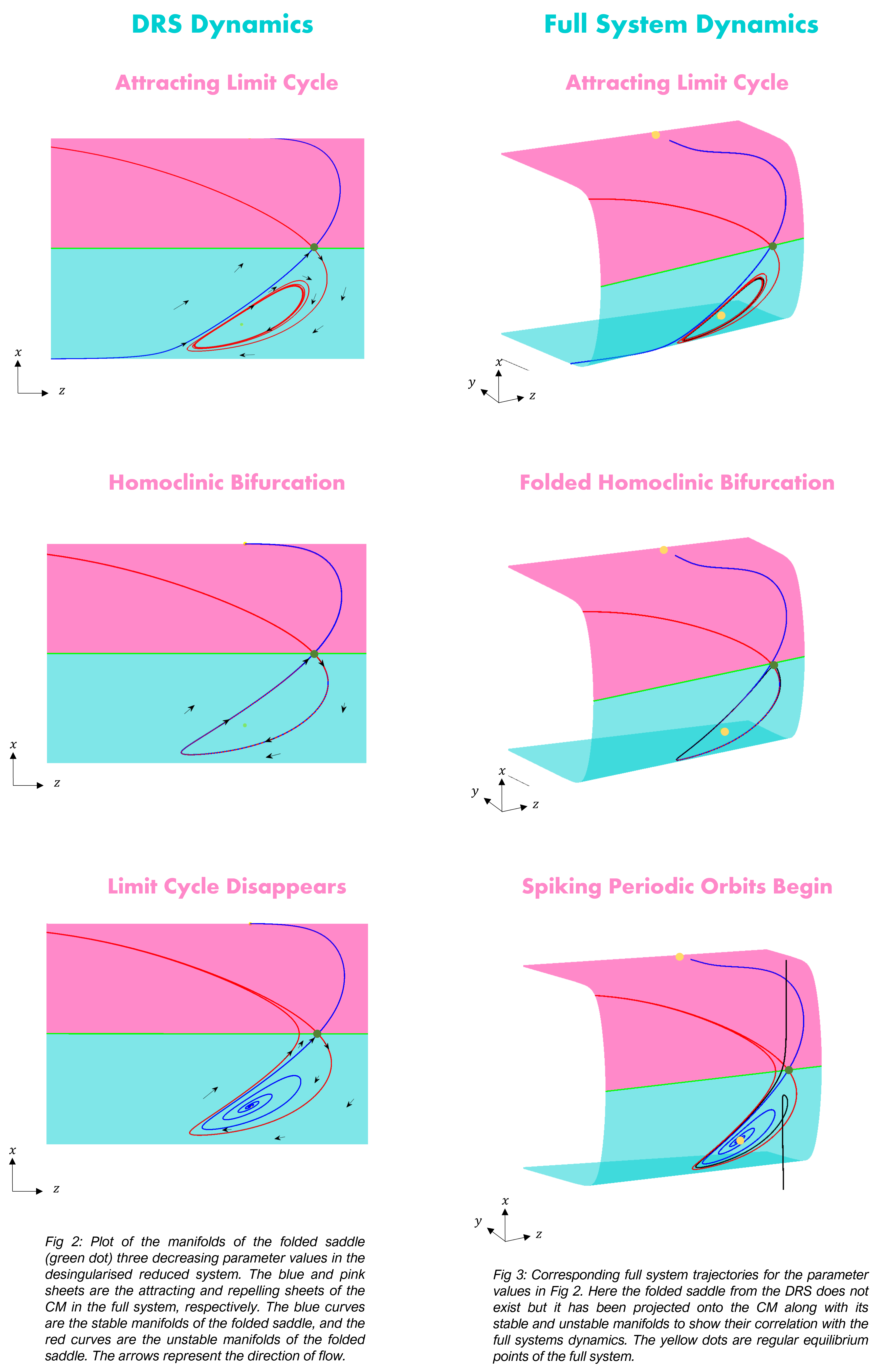
A folded homoclinic bifurcation occurs when a limit cycle of the DRS becomes homoclinic to a folded saddle in the DRS. To demonstrate how this affects the full system dynamics, we look at the dynamics of the DRS (Fig 2.) vs the dynamics in the full system (Fig 3.). I have projected the DRS saddle stable and unstable manifolds into the full system for visualization.

What we see is that prior to the homoclinic in the DRS the dynamics of both the DRS and full system tends toward the periodic solution that is present. As the DRS dynamics become homoclinic the full system dynamics collide with the position of where the folded saddle equilibrium would be; here is the point in which a folded homoclinic bifurcation takes place. Finally, as the DRS dynamics passes through the homoclinic bifurcation and the periodic solution disappears, the full system dynamics begins exhibiting bursting behavior. Further ‘collisions’ of these bursting solutions with the folded saddle results in further folded homoclinic bifurcations resulting in a spike added to the burst each time.

Currently, I am working on developing a return map for a generic folded homoclinic bifurcation. This involves a blow-up analysis of the folded saddle point in the full system to find a local part. I will then consider a global part for the map to help understand the differences in spiking behavior of the systems with an observed folded homoclinic bifurcation, to determine how much of these differences are due to the global features of the model’s geometry versus the local interaction of the limit cycle with the folded saddle.

References

[1] Desroches, M., Krupa, M., and Rodrigues, S. (2016). Spike-adding in parabolic bursters: the role of folded-saddle canards. Physica D: Nonlinear Phenomena, 331, pp. 58–70.

[2] Desroches, M., and Kirk, V. (2018). Spike-adding in a canonical three time-scale model: superslow explosion and folded-saddle canards. SIAM Journal on Applied Dynamical Systems, 17(3), pp. 1989–2017.