Adaptive Networks in Action: Opinion Formation, Epidemics and the Evolution of Cooperation
Nishant Malik (1,*) and Feng Shi (2,*)
1. Department of Mathematics, Dartmouth College, Hanover, New Hampshire 03755, USA
2. Odum Institute for Research in Social Science, University of North Carolina, Chapel Hill, North Carolina 27599, USA
* Both authors contributed equally.
This year's presidential election result may have surprised many: it seems that the majority of your friends and even friends of your friends agree with you on the choice of the candidate – but how did you become the minority in the end? Let's turn from the political reasons for this phenomenon to an analysis from a network perspective. We tend to form connections with people of similar minds, and simultaneously, our network connections influence our opinions and behaviors to become further homogenized groups. This feedback loop creates echo chambers; over time, the whole population segregates into local networks with very similar opinions, attitudes, and behaviors. On the macroscopic level, this process can lead to a highly polarized population with local, homogeneous groups. Although the result may not be pleasant, this adaptive process between opinion spreading and network tie formation is fascinating, and it is one representative example of an important topic in network science — adaptive networks.
Analogous to the above example about opinion formation during elections, the spread of infectious diseases is also a process that involves adaptive networks. Social, sexual or contact networks constrain the spread of an infectious disease; at the same time, individuals may break connections with infected persons either due to public interventions or voluntary isolation, thus changing the structure of the underlying network on which the disease spreads. In other words, the network adapts its structure in response to disease dynamics, and as the structure of the underlying network changes, disease dynamics are also affected.
Another significant area of research in adaptive networks is the evolution of cooperation in socio-economic systems. In such systems, individuals with competing strategies of either cooperation or defection interact with each other as a network, where nodes represent the individuals and edges represent the interactions. There is a payoff associated with every interaction, which adds up to one’s total payoff over time. Network structure also evolves, as defectors prefer to exploit interactions with cooperators while cooperators prefer to avoid defectors. Simultaneously, individuals update their strategies to improve the payoff by switching between cooperation and defection. This feedback between dynamics and network structure is what makes adaptive networks so exciting, and leads to emergence of many “critical” phenomena similar to that observed in nature and society.
Before proceeding further, let's try to make the idea of adaptive networks somewhat clearer. Networks are dynamic: they grow, shrink, and organize in different structures. If the dynamics are limited to the evolution of network structures only, then the problem is referred to as one of "dynamics of networks". If there is a dynamic process occurring on the network while the network structure remains static, then the problems is referred to as one of "dynamics on networks." Research in dynamics of networks focuses on implications of dynamics in shaping network structures – including rewiring of network ties [1], preferential attachment [2], and other deterministic or stochastic rules that update network structures. At the same time, research in dynamics on networks studies the impact of structural properties of networks on dynamic processes on those networks – such as the spread of epidemics [3,4], opinions [5], information cascades [6], evolutionary games [7], and synchronization of oscillators [8]. Unsurprisingly, the two lines of research eventually converged and gave birth to the subject of this article. In adaptive networks, both the states of nodes (or edges) and the structure of the network evolve in response to each other.

Fig. 1 Schematic illustrating the difference between dynamics on networks, dynamics of networks and adaptive networks.
In summary, an adaptive network system has two intertwining components -- an evolving network and a dynamic process on the network -- that co-evolve and affect each other (see Fig. 1). It is the coupling between the two components that distinguishes adaptive networks. Network systems with separable time scales between dynamics on and of networks – although they evolve over time – are not necessarily adaptive. For example, if the process occurring on a network happens much faster than the evolution of network structures, we can treat the process as though it is happening on a static network without worrying about the interplay between the process and changes in the underlying network structure. Consider road networks (places connected by roads) which change slowly over time: it makes sense to assume that a road network is static when studying the traffic flow on a timescale of hours to a few days.
To further illustrate studies on adaptive networks, let’s focus on three categories of adaptive systems that the authors are most familiar with.
Co-evolving voter model
Election results are the outcome of complex social dynamics, and an important component of these dynamics is the process of collective opinion formation. Two key ingredients involved in collective opinion formation are the following. First, people's opinions shape their social networks, since people tend to form ties with like-minded people. Second, people's opinions are influenced by their social networks due to, for example, peer pressure.
A model which incorporates these two key ingredients is the the co-evolving voter model, which was first developed by Holme and Newman [9]. In the simplest case, every node in a given network takes one of two possible opinions (e.g., conservative or liberal). Then, at each time step during the process, a pair of connected nodes is chosen at random. If they have the same opinion, nothing happens. Otherwise, with probability 1-α one node of the two will adopt the other’s opinion, and with probability α one node will sever this tie and connect to a random node in the network with the same opinion. Eventually, for a finite network the process will enter a frozen state where no connected nodes have different opinions.
There are many variants of this model, such as the one with multiple opinions [9-11], the one with more realistic rewiring rules [10-13], and so on. What makes this collection of models so appealing is the complex configuration to which each model converges, such as consensus or segregation, that resembles a pattern observed in real societies. Despite detailed network structures varying from model to model, a continuous phase transition is spotted as the parameter α (or its analogue) varies, implying rich dynamic properties of the process.
The transition divides the dynamics into two regimes. Above the transition point, the underlying network fragments into many disconnected components, with each component holding a different opinion, while below the transition point a giant component exists, dominated by one single opinion. The phase transition results from the competition between the two processes: opinion change and edge rewiring. Opinion change is a slow process, meaning that it takes many steps to enter freezing, and tends to consensus (cf. classic voter model [19]), while edge rewiring is fast and leads to fragmentation. Their co-evolution is found to follow a diffusion process by simulation [11,12]. In the end, it is the interplay between the two processes that drives the system into complex configurations of network topology and opinion distributions.
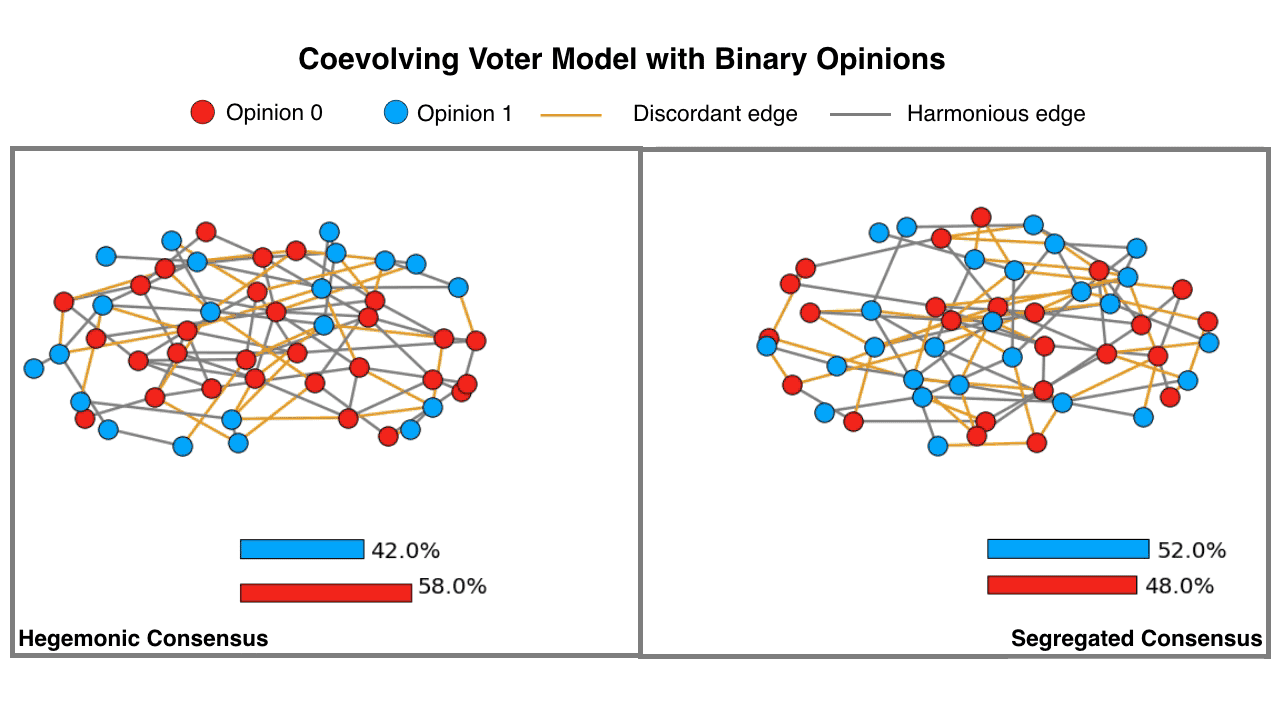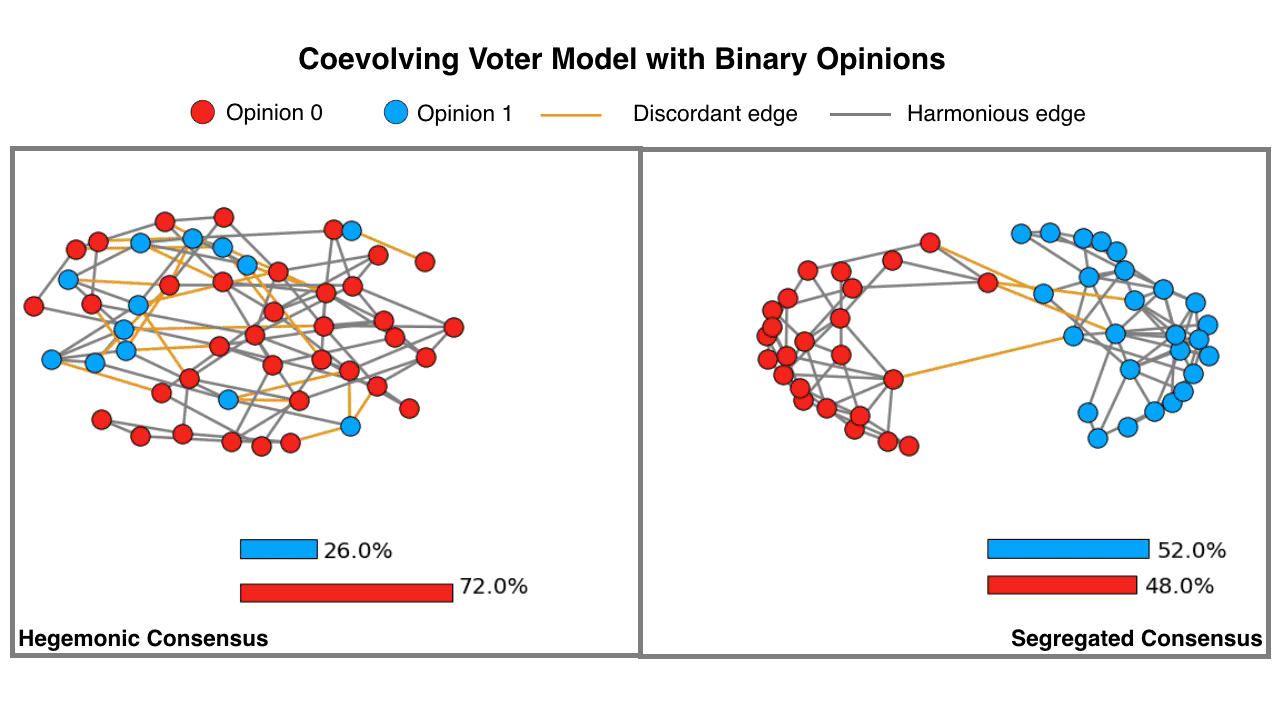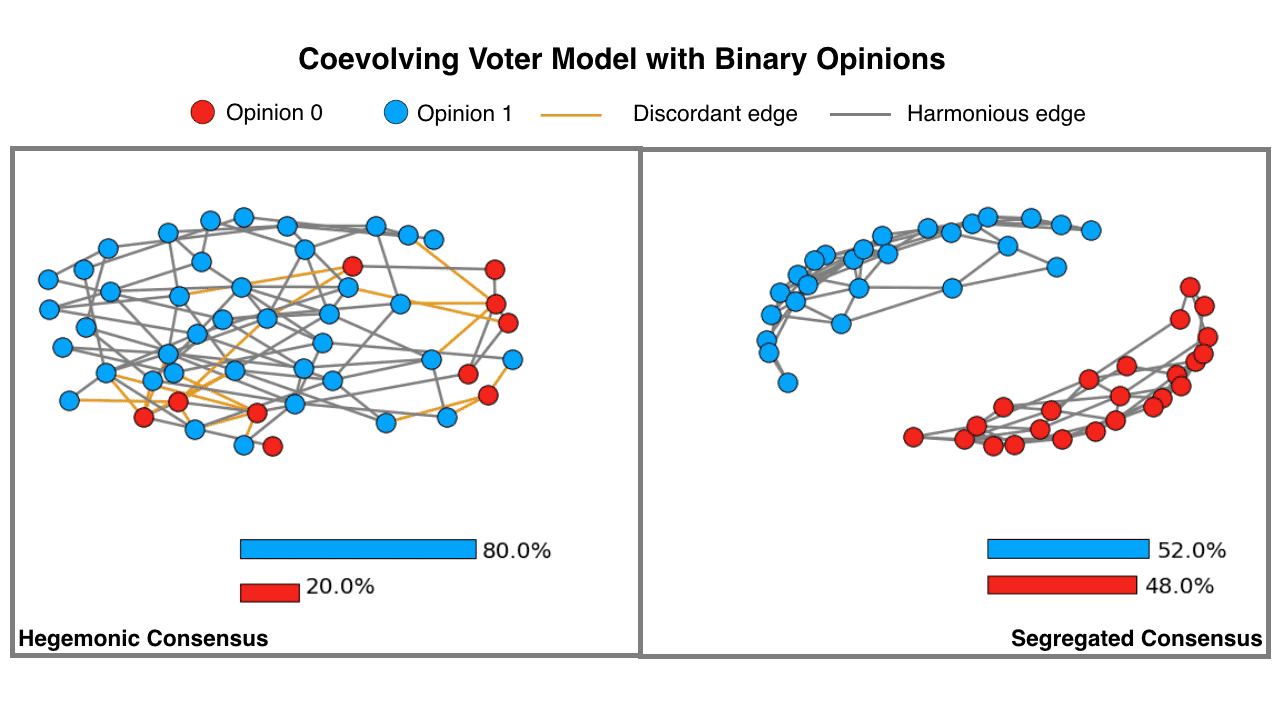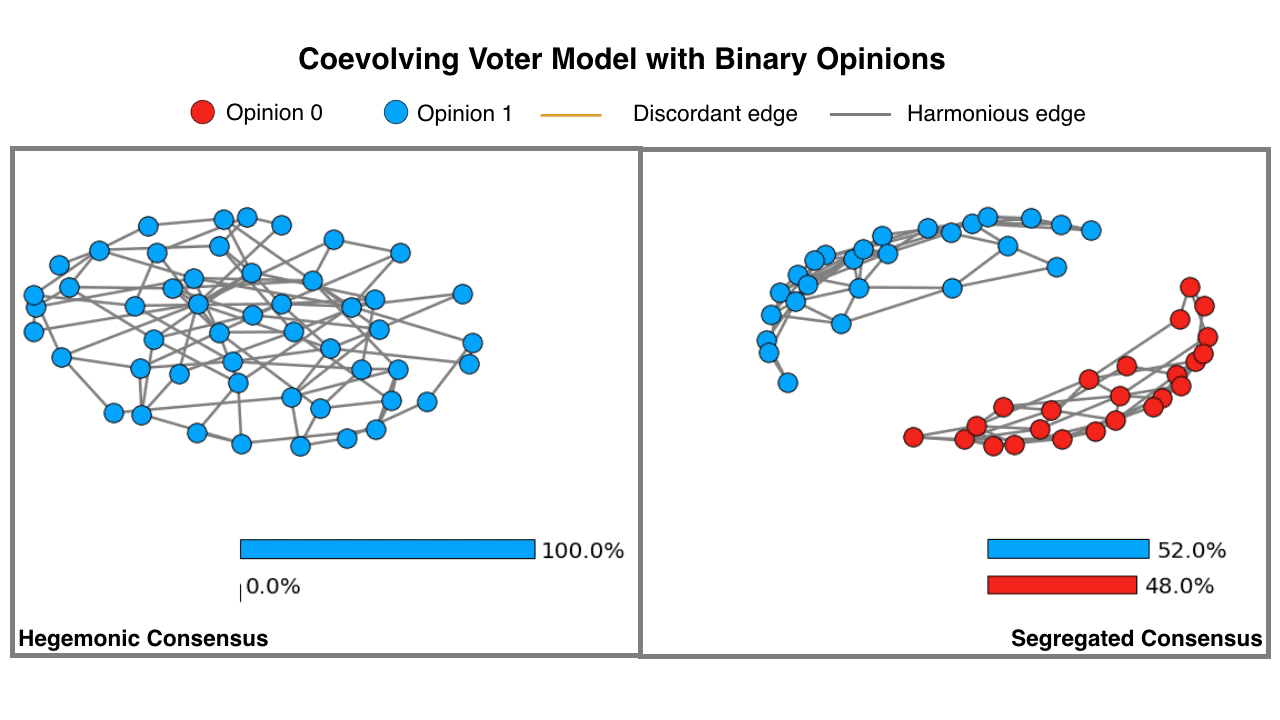
Fig. 2. An animation demonstrating the formation of two distinct types of consensus states in a coevolving voter model with binary opinions. The hegemonic consensus is the state when all the nodes hold the same opinion. Whereas, in the case of the segregated consensus, the underlying network disintegrates into two components, with nodes in each component holding opposing opinions. Note: If animation is not active, in most browsers you may right-click (or control-click) and select "open image in new tab" to view the animation.
Adaptive epidemic models
The co-evolving voter model treats all states of nodes equally; if we allow one state to be more “influential” than others, then we arrive at the susceptible-infected-susceptible (SIS) model in epidemiology. The simplest SIS model looks like the following: in a well-mixed population, every person is either susceptible to or infected by some infectious disease. A susceptible person in contact with an infected will be infected with probability γ but not the other way around, while infected persons will recover and turn back into susceptible with probability β. Evolution of epidemics can be described by a simple compartment model [20].
The assumption of a well-mixed population can be replaced by various model networks, yielding better understanding of disease prevalence. One of the key dynamic properties of this model is a phase transition as parameters γ and β vary. Below transition, the population is disease free, while above transition it approaches an endemic state.
If we continue to allow the underlying networks to change based on the states of people in the network, then we are dealing with adaptive SIS models. An intuitive way to introduce the coupling between disease dynamics and network topology is to allow every susceptible individual to break his or her tie with an infected person and rewire to a random susceptible person in the network with probability α. This additional step dramatically alters the dynamic behavior of the model. The phase transition becomes discontinuous, and more interestingly, a bistability region emerges above transition, where both disease free and endemic states are stable [14].
Evolutionary games on adaptive networks
The motivation for many decisions made by people and organizations is to maximize payoffs from the outcomes of those decisions. Game theory provides the mathematical tools to study the consequences of such motivations in socio-economic systems. In game theory, people and organizations are modeled as intelligent, rational agents who tend to cooperate or defect in making decisions.
Perhaps the best known game is Prisoner’s Dilemma (PD), where two players simultaneously choose between cooperation and defection. For either of the two players, the choice of defection always yields a higher payoff regardless of the action of the other player. Nonetheless, the collective payoff is maximum if both players choose to cooperate. PD models the social dilemma of choosing between personal gain via defection and group gain via cooperation.
Given that defection often yields a better personal payoff, as in the prisoner’s dilemma, how is it that cooperation is commonly observed in nature and society? This is a fundamental question in applications of game theory. In biology, especially, cooperation is a common phenomenon in biological systems from cells and organisms to animal societies. This question motivated the marriage between game theory and biology and led to the development of evolutionary game theory (EGT). In game theory, one’s action is determined by one's strategy – which is a function of one's own previous actions and those of the opponent. EGT introduces an additional element of "dynamics" by allowing strategies to evolve, and the evolution of cooperation can then be studied as games are played repeatedly among a large population.
In recent years, both classic games and evolutionary games have been studied in a network setting, where nodes represent players and edges represent games played among the players. The central question researchers are attempting to answer in these studies is: which combinations of game rules, dynamics, and network topologies can promote cooperation among selfish and unrelated individuals?
Adaptive networks add more realistic dynamics to the previous work by allowing network structures to change. For example, in the prisoner’s dilemma game on adaptive networks, the players can update their strategies based on their positions in the network, and they are also allowed to break links to defectors or form links to cooperators to improve their payoffs. Many studies involving evolutionary games on adaptive networks have found that co-evolution of network structures and individual strategies can give rise to robust cooperation among the players [15]. The explanation is intuitive. First, in most adaptive systems a player’s payoff depends on the actions of neighbors in the network (e.g., number of cooperative neighbors). Second, defectors are penalized by losing links. Hence players tend to maintain a cooperative neighborhood and cooperate at the same time. Interested readers can refer to Pacheco et al. (e.g., [16]) for an analytical treatment.
Similar to the adaptive voter model, networks adapted to evolutionary games also self-organize into complex topologies in the end, showing phenomena such as the division of labor and the emergence of social hierarchies [17]. Such stationary configurations are referred to as network Nash equilibria in a few studies.
Mathematical Challenges
A commonality among the examples above is the complex self-organizations in those adaptive systems. Computer simulations are widely used to identify interesting patterns in system dynamics and network structures. However, to be able to rigorously quantify and predict the dynamics, we need mathematical descriptions. Unfortunately, it is not always feasible to construct exact mathematical models and equations for those systems, not to mention analytical solutions. Adaptive network systems often involve many individual dynamical systems interacting through complicated rewiring rules, similar to a many-body problem for which we have yet to develop analytical solutions in general. The common trick used to get around this challenge is to convert a many-body problem to a few smaller, manageable problems through innovative approximations. Even though the approximations do not generate exact descriptions of the systems, they are often able to produce qualitatively similar behaviors to those identified by computer simulations, while remaining tractable.
The inspiration for these approximations emanates from a theory in physics known as the mean field theory (MF). In its most elementary form, mean field theory replaces the many influences from other nodes in a network on an arbitrary node by a single average influence. This incarnation of mean field approximation is an excellent tool for studying dynamics on dense static networks, but it performs poorly in the case of adaptive networks which are heterogeneous and evolving.
Models for adaptive networks need to keep track of the evolution of node states and network structures simultaneously. In many cases, it is not difficult to derive equations for the evolution of individual nodes, edges, triplets, and other low-order structures, but equations for higher-order structures consisting of more than a couple of nodes quickly become too complicated to write down. Hence approximations are necessary to make the system of equations tractable. Pair approximations (PA) and approximate master equations (AME) have seen successful application in real studies of adaptive networks.
Pair approximation reduces a multi-body system to the interaction between two simpler systems. For example, in the SIS model, the number of edges (two-body) between infected and susceptible individuals can be approximated by the density of infected individuals multiplied by the density of susceptible individuals (normalized appropriately); the number of connected triples (three-body) can be approximated by the product of the densities of corresponding edges (two-body), and so on. From this example, we can see that the approximation is precise when the network under consideration is random – which is rarely the case. One signature of those adaptive systems is their complex topologies. Therefore, although pair approximation manages to predict system behavior most of the time, the actual numbers resulting from prediction are way off from simulations.
The approximate master equations approach reorganizes the equations for the dynamics and network structures in a novel way. It groups nodes into compartments based on the degree of a node, the state of a node, and the number of neighbors of a particular state. Differential equations are then constructed to describe the evolution of these compartments. Since AME exploits fine details of the networks such as node degree, in general it provides more accurate results than pair approximations in capturing various features of adaptive network systems.
Last but not the least
Although the examples above originate from social systems, adaptive networks are ubiquitous in complex systems of biological, technological, and physical origins. In power grids, for example, when a transmission line fails, it may disrupt operations of nearby power stations, overload other transmission lines, and cause a cascade of failures. In our brains, effective connections between neurons constantly re-adapt to specific functions performed by the neural networks. Interested readers can consult Gross et al. [18] for a comprehensive review.
The states of nodes are not necessarily discrete – they can also be continuous, representing things such as the density of a species in a food web. Edges in networks may have dynamical systems associated with them as well, such as the amount of traffic flow on a certain road. When edges are dynamical systems, we face a whole new kind of adaptive network – one in which edges might not die or form but their weights will evolve over time, driven by dynamical processes, which effectively change the structures of networks.
As networks become a common tool in studying complex systems, knowledge of adaptive networks will be a key to understanding the complex topologies and near-critical behaviors of many real world systems. Furthermore, with a good understandings of how adaptive systems work, we can start to make systems with desired complex configurations from local, adaptive rules.
References:
[1] Watts, D. J. & Strogatz, S. J. (1998) Collective dynamics of “small world” networks. Nature 393, 440–442.
[2] Baraba`si, A. & Albert, R. (1999) Emergence of scaling in random networks. Science 286, 509–512.
[3] Kuperman, M. & Abramson, G. (2001) Small world effect in an epidemiological model. Phys. Rev. Lett. 86, 2909–2912.
[4] Pastor-Satorras, R. & Vespignani, A. (2001) Epidemic spread- ing in scale-free networks. Phys. Rev. Lett. 86, 3200–3203.
[5] Castellano, C., Vilone D. & Vespignani, A. (2003) Incomplete ordering of the voter model on small-world networks, Europhys. Lett., 63 (1), pp. 153–158.
[6] Hisakadoa, M., & Morib, S. (2016) Information cascade on networks, Physica A, Volume 450, 15, pp. 570–584.
[7] Santos, F.C. & Pacheco, J. M. (2005) Scale-Free Networks Provide a Unifying Framework for the Emergence of Cooperation, Phys. Rev. Lett. 95, 098104
[8] Barahona, M. & Pecora, L. M. (2002) Synchronization in small- world systems. Phys. Rev. Lett. 89, 054101-4. (doi:10. 1103/PhysRevLett.89.054101)
[9] Holme, P. & Newman, M.E.J. (2006) Nonequilibrium phase transition in the coevolution of networks and opinions, Phys. Rev. E 74, 056108.
[10] Malik, N. & Mucha, P. J. (2013) Role of social environment and social clustering in spread of opinions in coevolving networks, Chaos: Interdiscip. J. Nonlinear Sci. 23, 043123
[11] Shi, F., Mucha, P. J. & Durrett, R. (2013) R. Multiopinion coevolving voter model with infinitely many phase transitions, Phys. Rev. E 88, 062818.
[12] Durrett, R., Gleeson, J. P., Lloyd, A.L., Mucha, P.J., Shi, F., Sivakoff, D.,Socolar, J. E. S., & Varghese, C. (2012) Graph fission in an evolving voter model, PNAS 109, 3682–3687
[13] Malik, N., Shi, F., Lee, H.-W., & Mucha, P. (2016) Transitivity reinforcement in the coevolving voter model, Chaos: Interdiscip. J. Nonlinear Sci. 26, 123112
[14] Gross, T.,Dommar D’Lima C. & Blasius, B., (2006) Epidemic dynamics on an adaptive network. Phys. Rev. Lett. 96, 208701-4. (doi:10.1103/PhysRevLett.96.208701)
[15] Ebel, H. & Bornholdt, S. (2002) Coevolutionary games on networks. Phys. Rev. E 66, 056118. (doi:10.1103/ PhysRevE.66.056118)
[16] Pacheco, J. M, Traulsen, A. & Nowak, M. A. (2006) Coevolution of strategy and structure in complex networks with dynamic linking. Phys. Rev. Lett. 97, 258103-4.
[17] Holme, P. & Ghoshal, G. (2006) Dynamics of networking agents competing for high centrality and low degree. Phys. Rev. Lett. 96, 908701-4.
[18] Gross, T. & Blasius, B. (2008) Adaptive coevolutionary networks: a review. J. R. Soc. Interface 5, 259–271.
[19] Sood, V. & Redner, S. (2005) Voter Model on Heterogeneous Graphs. Phys. Rev. Lett. 94, 178701.
[20] Hethcote. H (2006) The Mathematics of Infectious Diseases. SIAM Rev. 42(4), 599–653.