Norman Zabusky, a pioneer in some of the most extraordinary developments in “experimental mathematics” and nonlinear science, passed away on 5 February 2018 in Beer Sheva, Israel. Norman played a major role in computational fluid dynamics and the importance of visualization. Most notably, however, he was a co-discoverer, along with Martin Kruskal, of the “soliton" [1], a robust, coherent localized solution of certain classes of nonlinear partial differential equations — a discovery that created a new paradigm. The seminal paper announcing this discovery appeared in a 1965 article in Physical Review Letters [2]. It led to the development of the Inverse Scattering Transform [3], a means by which certain classes of nonlinear partial differential equations can be shown to be exactly “integrable”, and thus analytically solvable, Hamiltonian systems. The IST gives a way to identify “action–angle” coordinates in which the flow dynamics becomes linear. This was a truly astounding finding: at that time, the number of exactly integrable nonlinear systems could be counted on one hand (e.g., two-body interactions and certain spinning tops).
The story of the soliton discovery provides a wonderful example of how large leaps in scientific understanding often come from curious investigators having the courage to tackle and try to understand anomalous results, rather than ignoring them. In this case, the observations were the curious behavior of a 1953 numerical “experiment" known for decades as the Fermi–Pasta–Ulam (FPU) problem, but historically more accurately characterized as the Fermi–Pasta–Ulam–Tsingou (FPUT) problem [4]. The goal of the numerical experiment was to confirm Fermi’s (where Fermi was modeling a suggestion of Debye) explanation for the finite thermal conductivity of solids. The solid was modeled as a lattice of coupled, weakly nonlinear springs. The argument was that the nonlinear nature of the spring forces would cause vibrations to spread to all modes and reach a state of thermal equilibrium, thereby inhibiting heat transfer. However, the mathematical experiment — the first computer experiment of its kind — showed that the spring vibrations did not thermalize. In fact, the evidence indicated that if the energy all started out in one of the low modes, it stayed with the low modes and exhibited a kind of recurrence. Kruskal and Zabusky, very young at the time, set out to explain this abnormality and took on the challenge of understanding these curious results. Because the energy stayed in modes that are long compared to the individual spring lengths, they approximated the discrete spring equations with a continuum limit and found that the difference in successive spring extensions satisfied a partial differential equation, the Korteweg–de Vries (KdV) equation, which was known to describe long waves in shallow water. Also known was that the KdV equation had traveling-wave pulse-like solutions. (Even before that, in the mid 19th century, such waves had been observed and studied experimentally by John Scott Russell.) Numerical computations of solutions of the KdV equation showed that an initial disturbance would break into a set of these traveling waves and then — in an enormous surprise — the traveling waves would pass through each other, unhindered except for a phase shift. Clearly, these coherent solitary waves, which they named “solitons’’, were not only very special, but indicated special and as-yet-undiscovered properties of the KdV equation itself. From that great insight, a whole new subject was born. This subject, the study of nonlinear waves, would have profound effects not only in mathematics but also in physics, chemistry, biology, geology, and optics. Solitons and integrable systems, in particular, provided a new paradigm in nonlinear science.
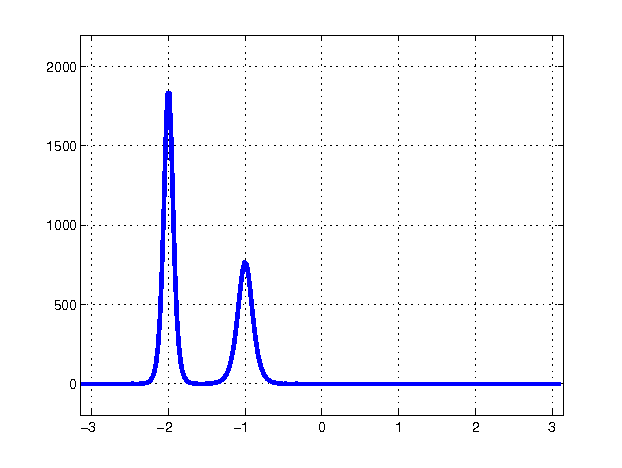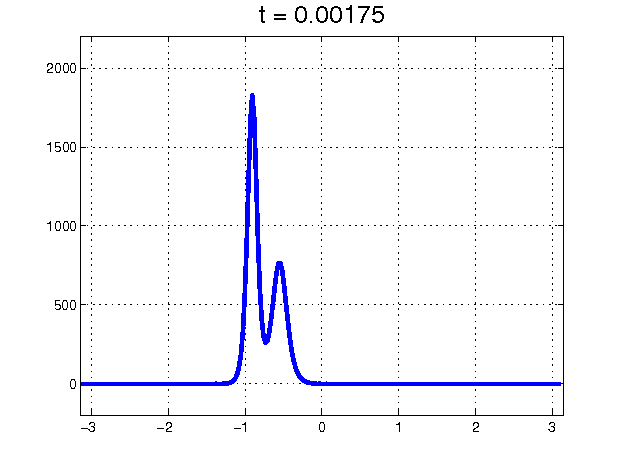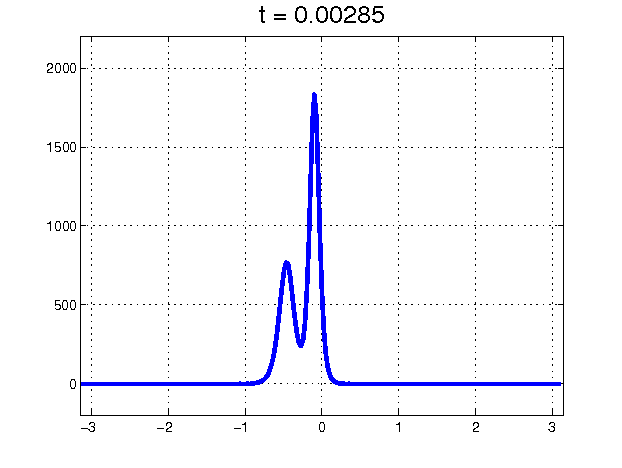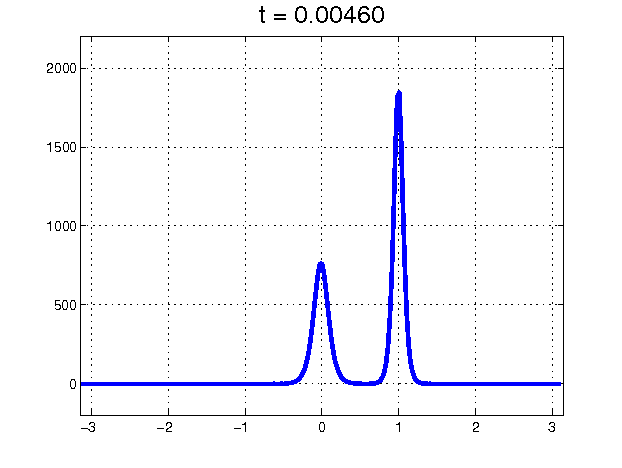
Figure 1: Collision between two soliton solutions of the KdV equation.
From the success of the computations of the KdV equation, Zabusky developed a keen appreciation of the importance of appropriate visualization and quantification as a tool in analyzing fluid dynamical and wave systems. In 1990, he and Francois Bitz introduced the term visiometrics, about which Zabusky wrote several papers, including an expository article in Physics Today [5] Zabusky often stressed visualization and even developed an interest in interactions with art. For example, in 2005, he organized the fourth Science and Art symposium (ScArt4).
Perhaps as significant as Norman’s scientific accomplishments was his steadfast, courageous support of human rights. He served on the Advisory Board of the Committee of Concerned Scientists, and he was a courageous and dedicated advocate of the Soviet Union’s “refuseniks" [6] , who suffered loss of jobs and were completely ostracized from society simply because they had requested to leave and build new lives in Israel and other countries. One of us was privileged to see Norman in action in these endeavors. Norman was visiting Kiev, where there were a series of conferences on nonlinear science between Soviet scientists and their Western counterparts from the late 1970s through the early 1990s. The conference in question, which took place in 1983, included such Russian luminaries as Zeldovich, Sagdeev, Arnold, Zakharov, Novikov, and occurred at a time of heightened tension between West and East. This did not deter Norman: He had many contacts with refuseniks and visited as many as he could, always under the disapproving scrutiny of the men in trenchcoats. He would sit down with these folk (usually over cups of chai), who had long felt that they had been forgotten. Norman would record everything they would say about themselves in great detail in his little notebook, and he did his best to give them the belief that they were not alone, that people of good will everywhere were aware of their plight (thereby giving them the courage to endure). For his efforts, Norman was punished. On a visit to Moscow the week after the Kiev Conference, he was informed that his safety could no longer be guaranteed and that he should immediately leave the Soviet Union. As Zabusky said at the time [6], “It is perfectly legal according to Soviet law,'' he said. “All I did was talk to them. I wanted to share my knowledge with younger and Jewish scientists who cannot get out.'' He said he wanted to visit the dissidents because “their lives and professional careers are truncated, and their harassment, especially in the Ukraine, you wouldn't believe.'' Thankfully, this story has a happy ending. Not only did many of those who were oppressed eventually find their way to new lives but, after Perestroika and Glasnost, Norman himself was invited back to the new Russia in 1989.
Norman J. Zabusky was born in Brooklyn, New York City on 4 January 1929 to Hyman and Anna (née Braun) Zabusky. He graduated from Brooklyn Technical High School and then attended City College of New York, from which he received a bachelor’s degree in electrical engineering in 1951. He then earned a master’s degree in electrical engineering from Massachusetts Institute of Technology in 1953 and a Ph.D. degree in theoretical physics from California Institute of Technology in 1959. His doctoral thesis concerned the stability of flowing magnetized plasmas. He held a postdoctoral position at the Max Planck Institute for Physics in Munich from 1959–1960. In 1960, he joined Princeton University as a researcher in the Plasma Physics Laboratory.
From 1961 to 1976, Zabusky worked at Bell Laboratories, where in 1968 he became the head of the first computational research department. In 1976, he became Professor of Mathematics at University of Pittsburgh. In 1988, he was named the State of New Jersey Professor of Computational Fluid Dynamics in the Department of Mechanical and Aerospace Engineering at Rutgers University. At Rutgers, he also founded and was Director of the Laboratory for Visiometrics and Modeling, and he held the Jacobs Chair in Applied Physics from 2000 to 2005. He retired from Rutgers University in 2006 and moved to Israel, where he was a visitor in the Department of Physics of Complex Systems at Weizmann Institute of Science.
For his many outstanding contributions, Norman Zabusky won numerous prestigious awards. In 1971, he received a Guggenheim Fellowship for his work in computational physics. He won the 1986 Potts Medal of the Franklin Institute for the discovery of the soliton. In 2003, Zabusky won the Otto Laporte Award of the American Physical Society, Division of Fluid Dynamics, “for pioneering and enduring contributions in nonlinear and vortex physics and computational fluid dynamics, including: the soliton; contour dynamics and V-states for 2D flows; vortex projectiles for accelerated inhomogeneous flows; and visiometrics for reduced modeling.”
Over the years, we enjoyed our many interactions with Norman Zabusky — whether as coauthor, discussant, debater, or host. His interests in both science (including visualization) and humanity were omnipresent and effervescent, and we and the rest of the scientific community will miss him.
References:
[1] N. J. Zabusky and M. A. Porter. Soliton. Scholarpedia, 5(8):2068, 2010.
[2] N. J. Zabusky and M. D. Kruskal.
Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States.
Phys. Rev. Lett.15,1965. 240.
[3] C. S. Gardner, J. M. Greene, M. D. Kruskal, and R. M. Miura, Method for solving the Korteweg–de Vries equation, Phys. Rev. Lett. 19 1095, 1967.
[4] T. Dauxois. Fermi, Pasta, Ulam, and a mysterious lady. Physics Today 61 (1), 55, 2008.
[5] N. J. Zabusky. Computational Synergetics. Physics Today 37(7) 36–46, 1984.
[6] New York Times article about talking to Refuseniks (Archives, 1983): Soviet expels U.S. professor who talked with dissidents.
Supplementary Reference: Wikipedia entry on Norman Zabusky.