
My ZomeTool [9] model of nested icosadodecahedra which I used to find reduced symmetry subspaces, before the wonderful world of equivariant bifurcation theory was introduced to me. :)
My journey thus far:
I completed my PhD in 2012 about the interaction between sound waves and laminar flames leading to thermoacoustic instability. My winding research journey since then took me first to Goettingen in Germany to work on pattern formation in transitional fluid flows such as plane Couette flow and inclined layer convection. In these fluid systems, I was exposed to the idea of mode interactions and the idea of invariant states being spatially/spatio-temporally localised patterns in addition to spatially extended patterns. Between 2015-2019 I was a research fellow at the University of Leeds where I worked with Prof. Alastair Rucklidge on the formation of spatially complex patterns such as superlattice and quasi- patterns. Since August 2019, I am a Hooke fellow at the Mathematical Institute, University of Oxford where my research focuses on the intersection of pattern formation and soft matter.
Soft matter crystallisation:
Soft matter systems abound in everyday life: from polymers and liquid crystals to biological materials such as proteins. Determining how such soft matter systems solidify/crystallise when cooled is important in a number of crucial applications ranging from formation of adhesives to designing materials for use in medical diagnostics. Soft matter has been observed to self-assemble into complex spatial patterns such as quasipatterns when they solidify as they are cooled from a melt. Soft matter crystallisation (SMC) is currently modeled at three scales: microscale - by tracking the dynamics of individual particles, phenomenologically - at the length and time scales of the full system or mesoscale - resolving only the effective interparticle interactions. An important research direction in this area is summed up by the question: `Given microscale information (e.g., shape of a polymer), can we deduce possible macroscale behaviour (e.g., observed patterns that the polymers self-assemble into)'?
Microscale computations are computationally intensive and preclude us from exploring vast regions of the parameter space or comparing different materials easily. On the other hand phenomenological models do not possess enough detail to explore possibly different mechanisms that govern self-assembly in different polymer systems. Therefore, an avenue of my recent and continuing research is to critically explore the limitations of a mesoscale model [1,2] and improve them to retain as much of the physics as is necessary. I rigorously repurpose computational methods and tools created from multiple areas of pure/applied mathematics such as topological data analysis, computational algebraic geometry and equivariant bifurcation theory in order to understand the formation of complex spatial patterns.
Using algebraic geometry:
Near the onset of crystallisation, equilibria can be determined by scaling the variable, parameters, space and time appropriately in a weakly nonlinear analysis. Such a weakly nonlinear analysis can be used to reduce the dimensionality of a system by distinguishing between dynamically active modes, which are growing or neutrally stable, and passive modes, which decay rapidly. Close to a phase transition, we can rewrite the dynamics in terms of amplitudes of different active wave vectors or active modes that make up a pattern. In doing so, this technique converts partial differential evolution equations into coupled ordinary differential equations describing time evolutions of each amplitude, i.e., amplitude equations. Equilibria for these amplitude equations can then be determined by solving the resulting coupled nonlinear polynomial equations. In the simplest cases, symmetry arguments can be used to decrease the number of coupled polynomial equations, whose solution may then be found in an iterative manner. The success of this method is dependent on a ‘good’ initial guess supplied and converges only to one solution at a time. However, my recent approach is to obtain all real solutions of the systems of polynomials using non-iterative homotopy methods that were developed using ideas from computational algebraic geometry. In recent works [3-5], I use homotopy methods [6] to solve for all real solutions of the amplitude equations. Such a non-iterative method allows us to ask more comprehensive questions about how solutions are born and vary both in their existence and stability characteristics as functions of the system parameters.
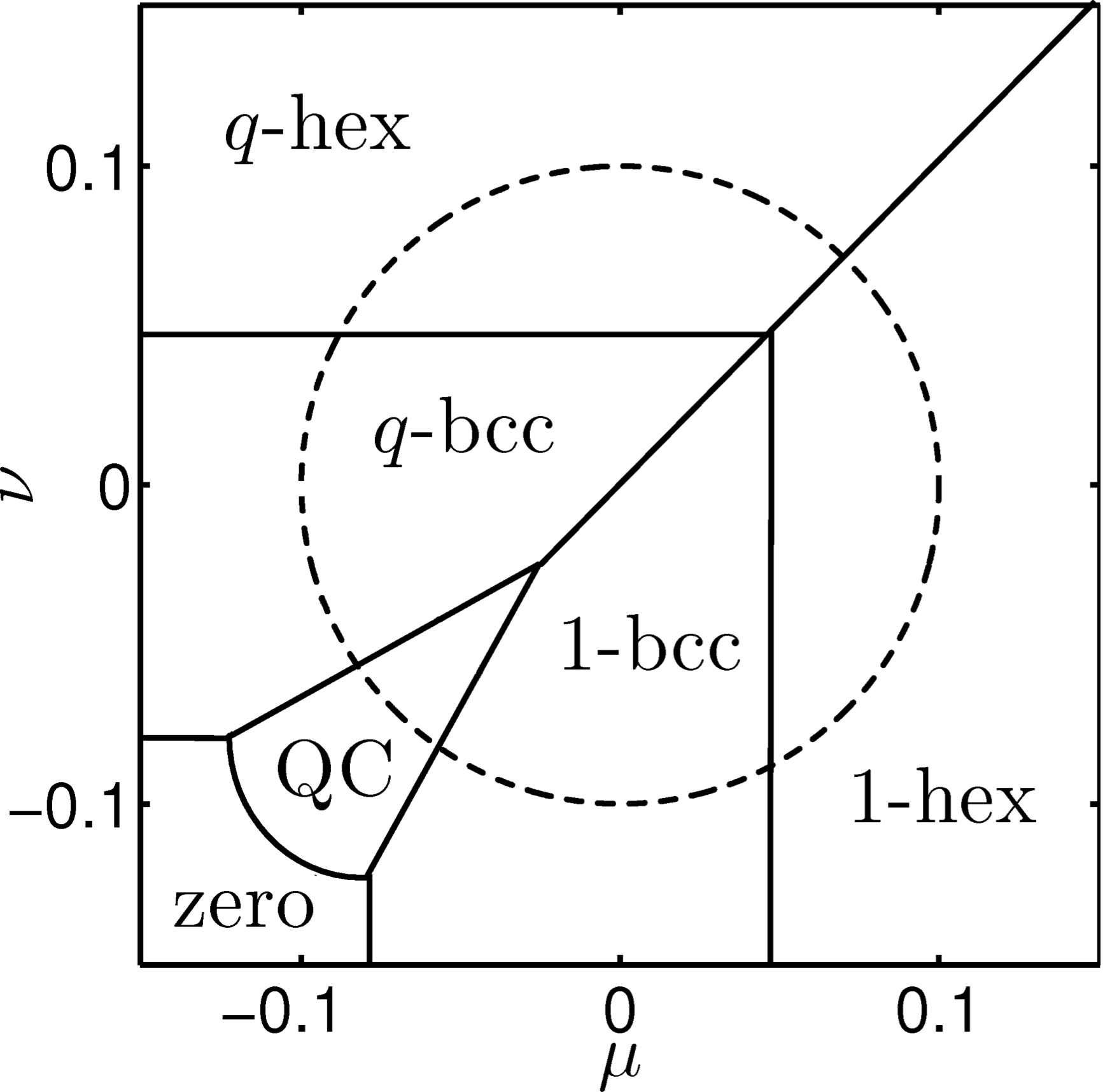

Figure 1: (a) 3D Structures with minimal specific free energy over a range of two system parameters, computed as equilibria of the amplitude equations using homotopy methods. 3D icosahedral quasicrystals are predicted to be globally stable in the third quadrant (consistent with timestepping results of the full partial differential equations of the model), (b) Example of variation in scalar density in a 3D icosahedral quasicrystal, sliced along the plane showing ten-fold symmetry [3].
In a minimal mesoscale model for soft matter crystallisation, [3] shows that 3D icosahedral quasicrystals are the globally stable state over a range of system parameters along with an example of a 3D icosahedral quasicrystal (Figure 1). Amplitudes of the wave vectors in this case were obtained by solving two coupled amplitude equations for the length scales in the problem. More than one real solution for the amplitudes is obtained at the same parameter and the state with the lowest free energy from among them is chosen as the globally stable state. This analysis enforced the assumption of full icosahedral symmetry for the quasicrystalline pattern. However, we can also consider symmetry broken cases and derive appropriate coupled amplitude equations and solve them using homotopy methods. Starting simulations from such symmetry broken solutions determined via the above method, I obtain two different periodic stackings of 2D decagonal QCs and an aperiodic stacking of 2D decagonal QC, in addition to the fully symmetric 3D icosahedral QC as asymptotic states (shown in Figure 2) [5]. These symmetry broken solutions are dynamically stable states at some parameter combinations. We would not have obtained them had we not considered symmetry broken amplitude equations and had a method that obtained all their equilibria.
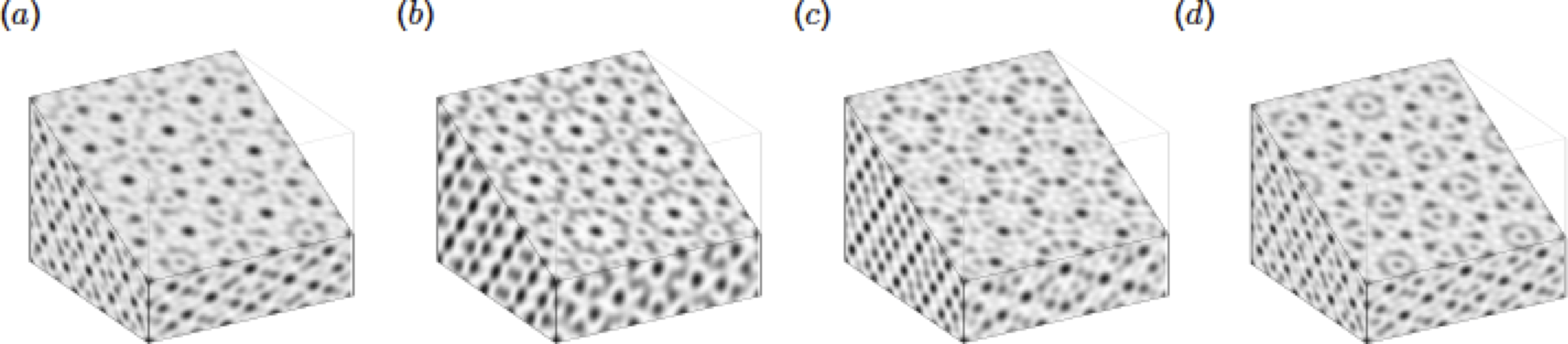
Figure 2: Variation of scalar density in a 3D soft matter system, sliced along the plane displaying the ten-fold symmetry, for extended dynamically stable states of (a) a fully symmetric icosahedral QC, (b) a periodic stacking of 2D decagonal QC with large stacking wavelength, (c) a periodic stacking of 2D decagonal QC with small stacking wavelength and (d) an aperiodic stacking of 2D decagonal QC [5].
Red Sock:
My recent Red Sock award at SIAM DS19 was for a poster that talked about using these homotopy methods to investigate competition between different second order mode interactions in creating superlattice patterns, such as those observed in Faraday wave systems [7]. Using this method system parameters for the birth of new superlattice solutions at pitchfork and saddle-node bifurcations were identified. It is also possible to analyse grid states [8] using this method. I am someone who is amazed that computations converge iteratively to even one solution from a good initial guess. Comparatively, a non-iterative homotopy method that obtains all real solutions sounds inspirational - inspirational enough to make me want to learn some algebraic geometry!
Outside research, I enjoy teaching and communicating mathematics to both students and the public. I have pursued this enthusiasm for public engagement through writing (The Conversation UK & IMA Mathematics Today), speaking (Cafe Scientifique & Otley Science Cafe) and participating (Big Draw London 2016, Queens of Industry Exhibition at Leeds Industrial Museum, British Science Festival 2019) in public outreach. I have benefited from multiple awards/fellowships aimed at promoting women's participation in science and I endeavour to pass the encouragement and support on by talking about my research journey at schools and universities and mentoring students. I believe that the generous social support at SIAM Dynamical Systems conferences for early career researchers is a great catalyst to attract/retain diverse talent in our community and I look forward to attending the next SIAM DS21 in Portland.
References:
1. A. J. Archer, D. J. Ratliff, A. M. Rucklidge and P. Subramanian, Deriving phase field crystal theory from dynamic density functional thory: consequences of the approximations, Physical Review E, 100-2 (2019), 022140.
2. D. J. Ratliff, A. J. Archer, P. Subramanian and A. M. Rucklidge, Which Wave Numbers Determine the Thermodynamic Stability of Soft Matter Quasicrystals?, Physical Review Letters, 123 (2019), 148004.
3. P. Subramanian, A. J. Archer, E. Knobloch and A. M. Rucklidge, Three-dimensional icosahedral phase field quasicrystal, Physical Review Letters, 117 (2016), 075501.
4. P. Subramanian, P. Riyapan and A. M. Rucklidge, Mode interactions and complex spatial patterns. Part I: Superlattice patterns, in preparation.
5. P. Subramanian, Exploring the phase space during self-assembly of a soft matter system, in preparation.
6. D. J. Bates, J. D. Hauenstein, A. J. Sommese and C. W. Wampler, Numerically solving polynomial systems with Bertini, SIAM (2013).
7. Y. Ding and P. Umbhanhowar, Enhanced Faraday pattern instability with three-frequency driving, Physical Review E, 73 (2006), 046305.
8. T. Epstein and J. Fineberg, Grid states and nonlinear selection in parametrically excited surface waves, Physical Review E, 73 (2006), 055302.
9. ZomeTool, website:
https://www.zometool.com/.