1. Who am I?

I am a postdoctoral researcher at the Mathematical Biosciences Institute, the Ohio State University. I was born in a remote yet historical part of India. The place is called Murshidabad, erstwhile capital of Nawab Siraj ud-Daulah, the last independent Nawab of Bengal. It is about 200 kms away from Kolkata, the present capital of the state of West Bengal, India. I completed my Bachelor of Science (B. Sc.) and Master of Statistics (M. Stat.) degrees in Kolkata. After spending a couple of years in the industry, I went to Technische Universität Darmstadt in Germany for my doctoral studies.

I am interested in stochastic analysis of complex systems that arise from various branches of sciences. Biological applications, in particular, fascinate me. They often reveal insightful connections among dynamical systems theory, probability theory and statistics.

2. Random dynamical processes on random dynamical structures

From an abstract point of view, many of the complex systems I study can be described as random dynamical processes on random dynamical structures. Think of a collection of agents each of which is endowed with a local state space (e.g., immunological statuses, such as susceptible, infected, and recovered, in case of an epidemic, political opinion, queue lengths at various service stations, magnetic dipole moments of atomic “spins” in models of ferromagnetism, buffer availability of a video chunk in peer-to-peer video streaming systems). The agents change their local states dynamically as they interact with other agents. Now, think of the agents as vertices of a graph. Then, the interactions among the agents can be described by the connections (edges between vertices) in the graph. See Figure 1 for an example from infectious disease epidemiology. Because the interaction patterns could change over time (e.g., due to preventive measures such as social distancing against COVID-19), the graph itself evolves dynamically.

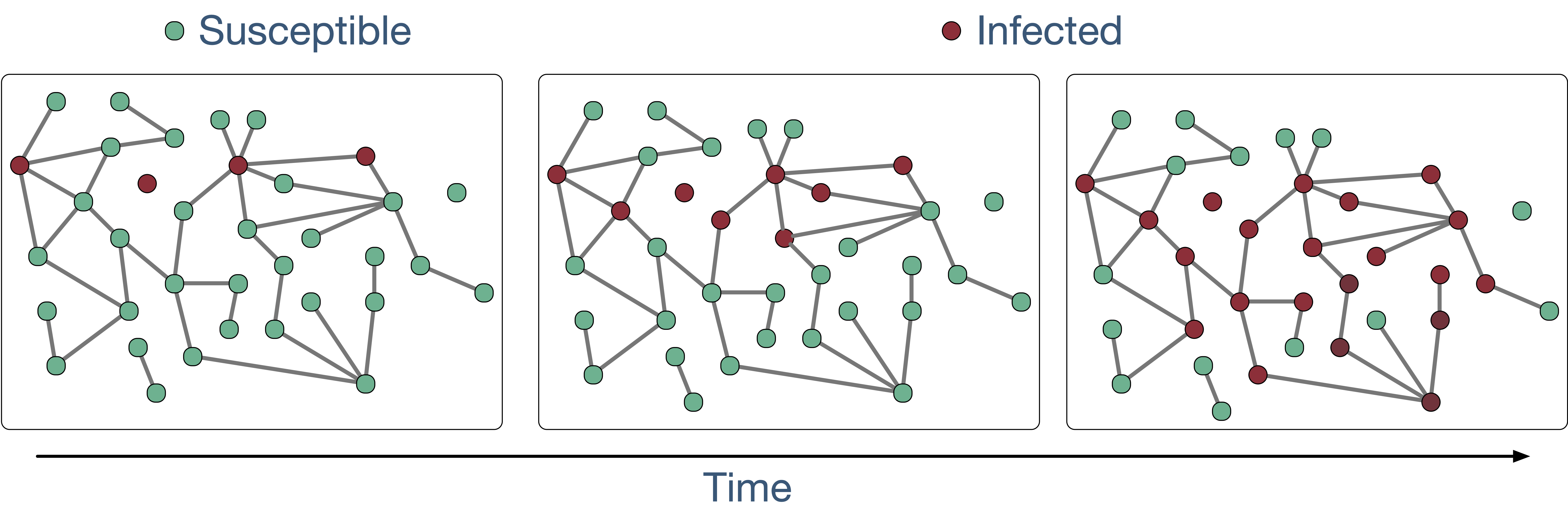
Figure 1. Stochastic Susceptible-Infected (SI) model. Susceptible vertices are shown in green and infected vertices, in dark red. Infected vertices infect their neighbours at a fixed rate [2]. From a statistical physics perspective, the above describes percolation over a graph, where the wet vertices are shown in dark red. As time progresses, the dark red component of the graph, sometimes called the percolated component, grows in size.

Exact stochastic analysis of such complex systems becomes cumbersome as the size of the graph grows large. Therefore, we need large-graph approximations. Functional Laws of Large Numbers (FLLNs) in the form of Ordinary Differential Equations (ODEs) or Partial Differential Equations (PDEs), Functional Central Limit Theorems (FCLTs) in terms of Stochastic Differential Equations (SDEs) or Stochastic Partial Differential Equations (SPDEs), and Large Deviations Principles (LDPs) are typical theoretical results that provide such approximations. I spend a lot of time deriving such large-graph approximation theorems. Those theorems are useful not only from a mathematical perspective, but also for statistical purposes. For instance, Dynamic Survival Analysis (DSA) is a method that converts those limiting dynamical systems in the form of ODEs or PDEs into prob- ability laws that can be used to derive likelihood functions for statistical inference.

3. Dynamic Survival Analysis

The DSA method [1] combines classical dynamical systems theory and survival analysis from statistics. In essence, it allows one to describe individual-level (micro-scale) dynamics in terms of population-level (macro-scale) dynamics. The population-level dynamics are typically described by large-graph limiting ODEs or PDEs. In the context of infectious disease epidemiology, the mathematical underpinning is provided by a novel application of the Sellke construction, which describes an epidemic process in terms of timings of individual infection and recovery as opposed to counts of individuals with different immunological statuses. In the general context, the DSA method extracts probability laws for the fate of a single individual agent (vertex) in a large graph. The probability laws are then used for likelihood-based parameter inference.

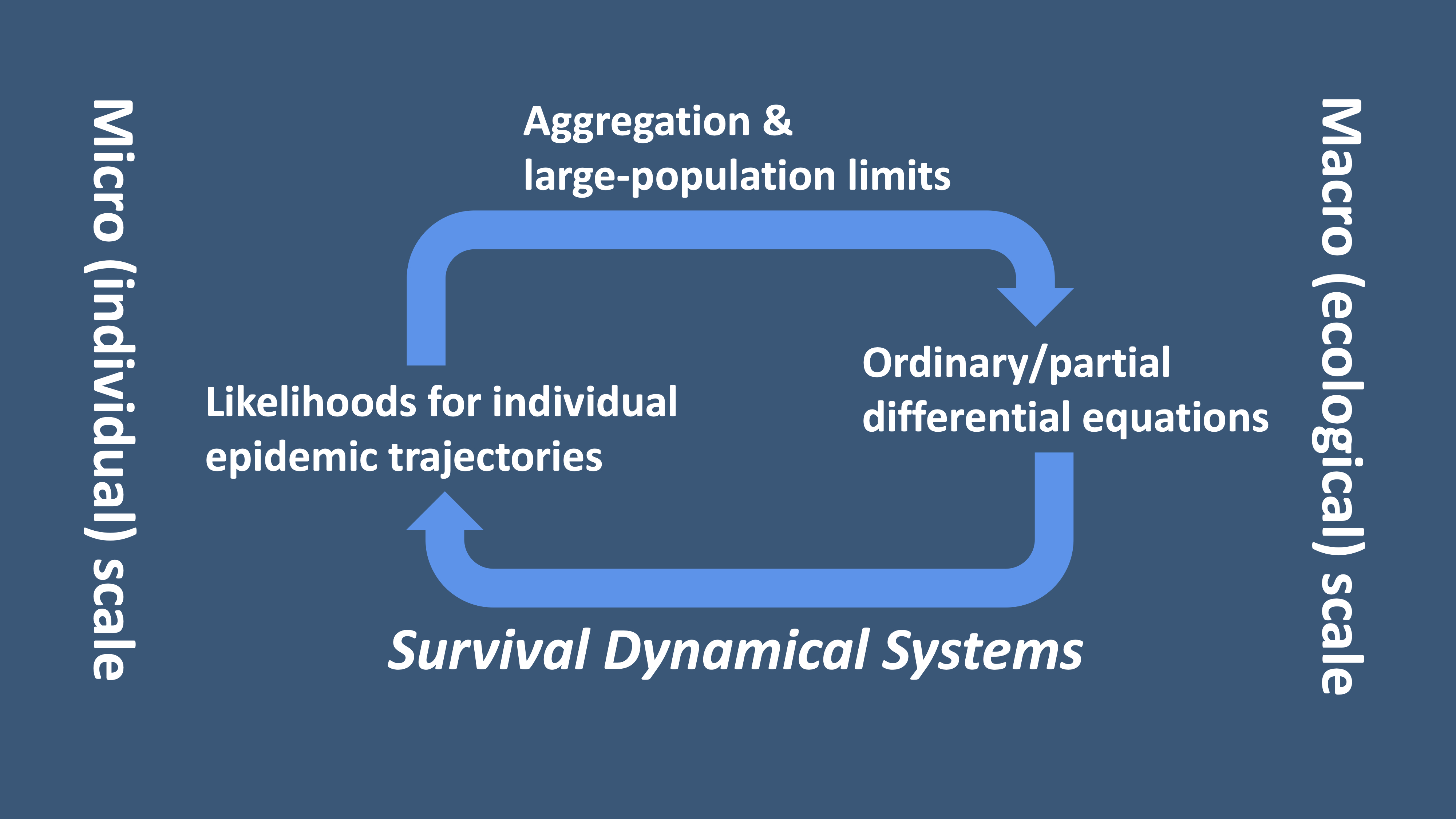
Figure 2. The DSA method interprets population-level dynamical systems as Survival Dynamical Systems (SDSs) [1], which describes probability laws for the fate of a single individual in a large population.

The DSA method was instrumental in the response modeling efforts [3] of the Ohio State University (OSU)/Infectious Diseases Institute (IDI) against COVID-19 in the state 

of Ohio. The response modeling team provided decision analytic support to the Governor’s Office, the Ohio Department of Health (ODH), and the Ohio Hospital Association (OHA).

Apart from doing mathematics, I enjoy eating delicious food, playing cricket and badminton, listening to music, and traveling. Even though I do not get much time to read literature nowadays, some of my heroes are actually writers. Rabindranath Tagore and Nazrul Islam, two prolific poets of Bengali literature, had the biggest influence on me during my formative years. Even today, they continue to shape my philosophy towards life.

References

[1] W. R. KhudaBukhsh, B. Choi, E. Kenah, and G. A. Rempała. Survival dynamical systems: individual-level survival analysis from population-level epidemic models. Interface Focus, volume 10(1):p. 20190048, 2020.

[2] W. R. KhudaBukhsh, C. Woroszylo, G. A. Rempała, and H. Koeppl. Functional Central Limit Theorem For Susceptible-Infected Process On Configuration Model Graphs. arXiv preprint: https://arxiv.org/abs/1703.06328.

[3] OSU / IDI COVID-19 Response Modeling Team. Predicting covid-19 cases and subsequent hospital burden in Ohio. 2020. Available: https://idi.osu.edu/assets/pdfs/ covid_response_white_paper.pdf.