S. Redner, Dynamics of Voter Models on Simple and Complex Networks, Santa Fe Institute, 1399 Hyde Park Road, Santa Fe, NM, 87501 USA.
How do groups of people come to consensus? While it’s hard to imagine a large group being able to agree on anything, there are some settings where unanimity is necessary—juries are one example. The voter model (VM) represents an idealization of this opinion evolution in which each individual, or agent, is influenced only by other members of the group; there is also no notion of a “right” or a “wrong” opinion, and there are no external influences, such as news media. In the VM, each agent, or voter, can assume one of two states (e.g., /, normal/mutant, Democrat/Republican). One agent resides at each node of a lattice or an arbitrary network and updates its state at unit rate until a population of agents necessarily reaches consensus.
In detail, VM evolution is as follows (Fig. Figure 1):
An anthropomorphic interpretation of VM dynamics is that each agent has zero self-confidence and merely adopts one of its neighbor’s state. We also discuss the related invasion process (IP), whose update rule is:
Pictorially, an invader dictatorially imposes its state on one of its neighbors; equivalently, an invader replicates and its offspring replaces a neighboring agent. While the differences between these two models appear superficially trivial, they are fundamental on complex networks. The two basic questions that we will discuss are: (i) What is the time to reach consensus? (ii) By what route is consensus achieved? We present our collaborative work on this subject with Vishal Sood and Tibor Antal [1].
A crucial feature of VM and IP dynamics on arbitrary networks is that they satisfy conservation laws that determine their long-time behaviors. Let’s develop the language to uncover these laws [2, 3]. Define as the state of the entire network, and , which can equal or , as the state of node . In an update, the node state changes from to or vice versa. Let denote the network state after the node at changes state. We may succinctly write the transition probability that node changes state as
\begin{equation}
\label{master}
\textbf{P} [\eta \to \eta_{x}] =
\sum_{y} \frac{A_{x y}}{N\mathcal{Q}}\,[\Phi(x,y)+\Phi(y,x)],
\tag{1}\end{equation}
where if the states at and differ and if these states agree, and is the adjacency matrix. Although this equation looks formidable, its meaning is simple: is non-zero only when nodes and are connected and in opposite states, so that an update actually occurs. For the VM, the factor accounts for first choosing any node with probability , and then one of its neighbors with probability , where is the degree of node . In the IP, : first choose node (a neighbor of ) with probability , and then choose with probability .
The kernel for the evolution of the population is the average change in the state of a single node, \(\langle \Delta\eta(x)\rangle\). This change equals the probability that \(\eta(x)\) changes from \(\mathbf{0}\) to \(\mathbf{1}\) minus the probability of a change from \(\mathbf{1}\) to \(\mathbf{0}\): \(\langle\Delta\eta(x)\rangle = \left[1-2\eta(x)\right] \mathbf{P}[\eta\rightarrow\eta_x]\). Summing this transition probability over all nodes gives the average change in \(\rho\), the density of nodes in state \(\mathbf{1}\):
\begin{equation}
\label{drho-av}
\langle \Delta \rho\rangle = \sum_x \langle \Delta \eta(x)\rangle =
\sum_{x,y} \frac{A_{x y}}{N\mathcal{Q}} \left[\eta(y)-\eta(x)\right]\,. \tag{2}\end{equation}
Since \(\mathcal{Q}\) is constant on regular lattices, the summand on the right is antisymmetric in \(x\) and \(y\) and \(\langle \Delta\rho\rangle=0\). Thus \(\langle\rho\rangle\) is conserved. This innocuous-looking conservation law has far-reaching consequences. It immediately gives the fixation or exit probability, namely, the probability \(\mathcal{E}(\rho)\) that a finite system with an initial density \(\rho\) of \(\mathbf{1}\)s attains a consensus of \(\mathbf{1}\)s. Because \(\rho\) is conserved and because the final state consists of either all \(\mathbf{1}\)s or all \(\mathbf{0}\)s, we have \(\rho=\mathcal{E(\rho)}\cdot \mathbf{1}+ [1-\mathcal{E}(\rho)]\cdot\mathbf{0}\). Thus, with no calculation the fixation probability equals \(\rho\)!
The power of this conservation law suggests looking for analogous laws for the VM and the IP on degree-heterogeneous networks. To obtain a conserved quantity, the factor \(\mathcal{Q}\) in the denominator of the transition rate in (1) must somehow be canceled out. This leads us to generalize the notion of density to the degree-weighted moments (note that and for simplicity we write as ), where is the density of s on the subset of nodes of degree the prime restricts the sum to nodes of degree . Here is the moment of the degree distribution of the network, with () the number (density) of nodes of degree . Repeating the calculation in Eq. (2) for for the VM and for for the IP, it is immediate to show that the conserved quantities are
\begin{align} \begin{split} \label{cons}&\langle\omega\rangle \qquad \qquad ~~\,\, \text{VM},\\ &\langle\omega_{-1}\rangle \qquad\qquad\text{IP}. \end{split} \tag{3} \end{align}
Since the initial value of the conserved quantity equals its value in the final unanimous state, the exit probability is
\begin{align} \begin{split} \label{exit-cons} &\mathcal{E}(\omega)=\omega ~~~~~\,\, \qquad \qquad \text{VM},\\ &\mathcal{E}(\omega_{-1})=\omega_{-1} \qquad \qquad \text{IP}. \end{split} \tag{4}\end{align}
An instructive example is the star graph, where nodes are connected only to a single central hub. For the VM, if the hub is in state and all other nodes are in state , then (4) mandates that the probability of reaching consensus is 1/2 ! That is, a single well-connected agent largely determines the final state. Conversely, in the IP, a mutant at the hub is very likely to be extinguished (fixation probability ), while a mutant at the periphery is more likely to persist (fixation probability ).
III. VOTER MODEL ON NETWORKS
To understand the VM and the IP on complex networks, first consider the complete graph, where the VM and the IP are identical. In each update event, , with , corresponding to a voter undergoing the respective state changes or . The probabilities for these respective events are
\begin{align} \label{rl}
\begin{split} \mathbf{R}(\rho)&\equiv \mathbf{P}[\rho\rightarrow\rho+\delta
\rho] = (1-\rho)\rho \\ \mathbf{L}(\rho)&\equiv \mathbf{P}[\rho\rightarrow\rho
-\delta \rho] = \rho(1-\rho)\,. \end{split} \tag{5}\end{align}
We term and as the raising and lowering operators.
We now use these transition probabilities to write the evolution equation for the average time to reach consensus when the fraction of agents initially in state is (the backward Kolmogorov equation [4, 5]):
\begin{eqnarray} \label{T} T (\rho)&=\delta t + \mathbf{R}(\rho)T(\rho\!+\!\delta\rho) +\mathbf{L}(\rho) T(\rho\!-\!\delta\rho) \nonumber\\ &+ [1-\mathbf{R}(\rho)-\mathbf{L}(\rho)] T(\rho)\,. \tag{6} \end{eqnarray} This simple-looking, but deceptively powerful equation expresses the average consensus time as the time for a single update step plus the average time to reach consensus after this update. The three terms account for the transitions or , respectively. Expanding Eq.(6) to second order in gives \begin{equation} \label{T-back} v(\rho)\frac{d T(\rho)}{d\rho}+D(\rho)\frac{d^2 T(\rho)}{d\rho^2} = -1\,, \tag{7}\end{equation} with drift velocity and diffusivity . On the complete graph, the drift term is zero and only the diffusion term, which quantifies the stochastic noise, remains. For the boundary conditions (consensus time equals 0 if the initial state is consensus), the solution is \begin{equation} \label{VM:KG:contime:sol} T(\rho)= -N\big[(1-\rho)\ln(1-\rho)+\rho\ln \rho\big] . \tag{8} \end{equation} For equal initial densities of each opinion, , while for a single mutant, . The linear dependence on represents the generic behavior for the consensus time of the VM on Euclidean lattices in spatial dimensions .
B. Complete Bipartite Graph
An important clue to understanding how degree heterogeneity affects the dynamics is provided by studying the simplest network network that contains of nodes with different degrees—the complete bipartite graph . In this graph, nodes are partitioned into two subgraphs of size and (Fig. 2). Each node in subgraph links to all nodes in , and vice versa. Thus nodes all have degree , while nodes all have degree .
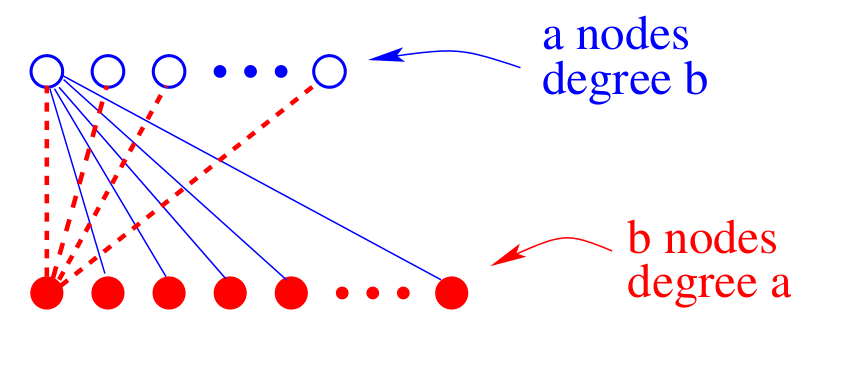
To determine the dynamical behavior, let be the respective number of voters in state on each subgraph, with , the respective subgraph densities. In an update, these densities change according to the raising/lowering transition probabilities,\begin{equation*}\label{VM:BG:jump} \begin{split} \mathbf{R}_\mathbf{a} \equiv \mathbf{P}[\rho_\mathbf{a},\rho_\mathbf{b} \rightarrow \rho_\mathbf{a}^+,\rho_\mathbf{b}] = \frac{a}{a+b}\,\,\rho_\mathbf{b}
(1-\rho_\mathbf{a}), \\ \mathbf{L}_\mathbf{a} \equiv
\mathbf{P}[\rho_\mathbf{a},\rho_\mathbf{b} \rightarrow \rho_\mathbf{a}^-,
\rho_\mathbf{b}] = \frac{a}{a+b}\,\, \rho_\mathbf{a} (1-\rho_\mathbf{b}),
\end{split} \end{equation*}
with . Here is the probability to increase the number of s in subgraph by 1, for which we need to first choose an agent in state in and then an agent in state in . Similarly, gives the corresponding probability for reducing the number of s in . Analogous definitions hold for and by interchanging .
From these transition probabilities, the rate equations for the average subgraph densities are and . Their solutions show that the subgraph densities are driven to the common value in a time of order 1 (Figure 3(a)). Thus the total density of s, which evolves as , becomes conserved in the long-time limit. Therefore, there is a two time-scale approach to consensus: initially, the effective bias quickly drives the system to equal subgraph densities ; subsequently, diffusive fluctuations drive the population to consensus. This dynamical picture also arises for general complex networks.
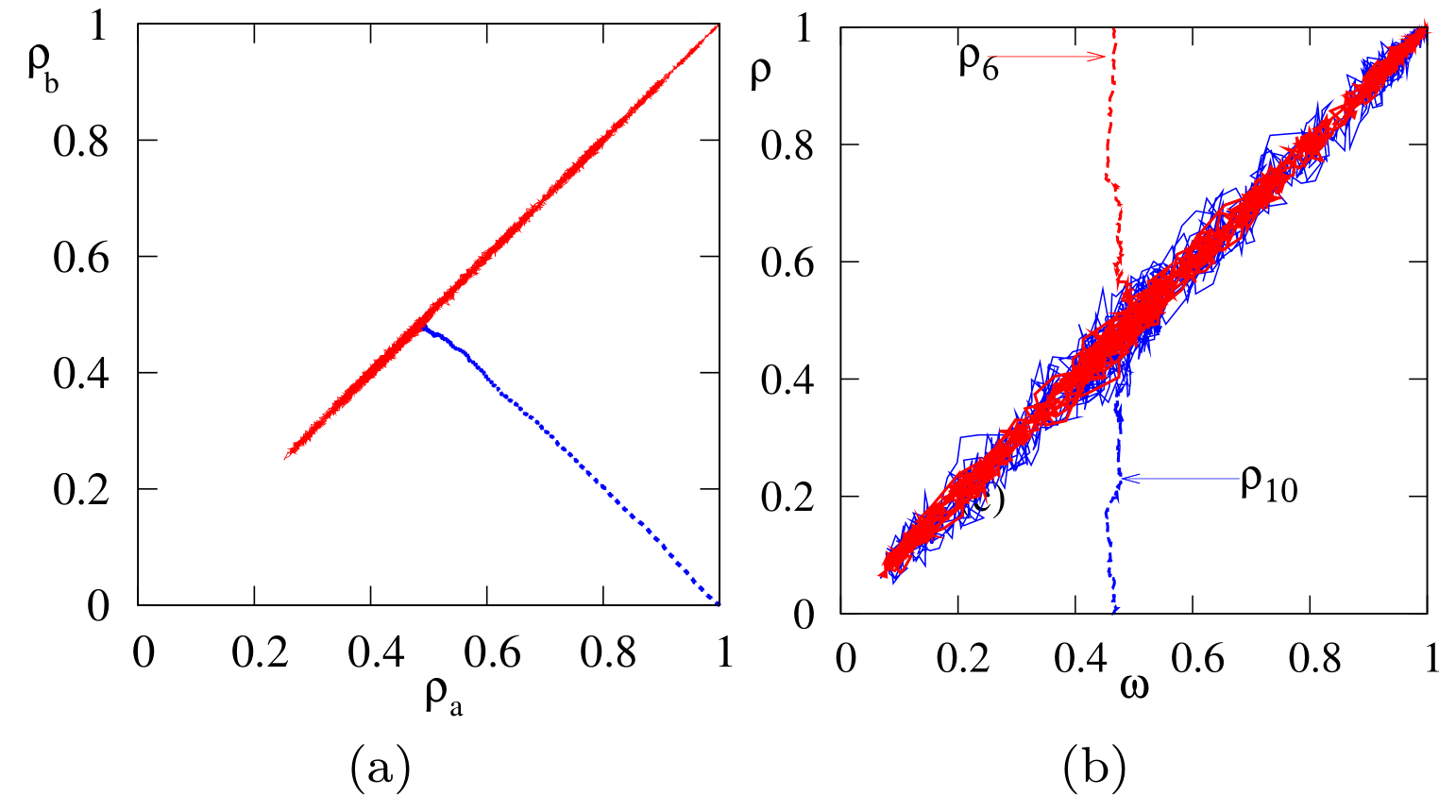
To determine the consensus time \(T(\rho_\mathbf{a},\rho_\mathbf{b})\), we exploit the feature that \(\rho_\mathbf{a}\to \rho_\mathbf{b}\) in the long-time limit. Then following exactly the same steps as those for the complete graph, the consensus time satisfies
\begin{equation} \label{VM:BG:CT:omega:eq} \omega (1-\omega)\frac{\partial^2T}{\partial\omega^2} =-\frac{4ab}{a+b}\,, \end{equation} with solution, for \(T(0)=T(1)=0\),
\begin{equation} \label{VM:BG:CT:sol} T(\omega)= \frac{4 a b}{a+b} \left[(1-\omega)\ln(1-\omega) +\omega\ln\omega\right] . \end{equation} The consensus time has the same form as in the complete graph [Eq. (\ref{VM:KG:contime:sol})], but with an effective population \(N_{\mathrm{eff}} = 4ab/(a+b)\). If both the \(\mathbf{a}\) and \(\mathbf{b}\) subgraphs have similar sizes, \(a, b\approx N/2\), then \(N_{\rm eff}\approx N\). However, if, for example, \(a\sim \mathcal{O}(1)\) and \(b\approx N\) then \(T\sim \mathcal{O}(1)!\) One highly-connected node can promote consensus.
C. Complex Networks
Now we turn to VM and IP dynamics on complex networks. While the bookkeeping becomes a bit tedious, the approach is the same as that for the complete bipartite graph: separate the dynamics according to the degree of each node. From Eq. \eqref{master}, the transition probabilities for increasing and decreasing the density of voters of type \(\mathbf{1}\) on nodes of fixed degree \(k\) are \begin{equation} \label{VM:HG:jump} \begin{split} \mathbf{R}_k[\{\rho_k\}] &\!\!\equiv\!\! \mathbf{P}[\rho_k\rightarrow\rho_k^+] = \frac{1}{N} \sideset{}{'}\sum_{x,y}\!\frac{1}{k_{x}}\, A_{xy}\,\Phi(y,x)\\ \mathbf{L}_k [\{\rho_k\}] &\!\!\equiv\!\! \mathbf{P}[\rho_k\rightarrow\rho_k^-] = \frac{1}{N} \sideset{}{'}\sum_{x,y}\!\frac{1}{k_{x}}\, A_{xy}\, \Phi(x,y), \end{split} \end{equation} where \(\rho_k^{\pm}=\rho_k\pm N_k^{-1}\), and the prime restricts the sum to nodes of fixed degree \(k\). In this equation, the densities associated with nodes of degrees \(k'\ne k\) are unaltered.
We now make the simplification of considering the mean-field configuration model (see, e.g., [6]). This is a network that is constructed by starting with a set of nodes that have "stubs'' of specified degrees, and then connecting the ends of stubs at random until no free ends remain. By this construction, the degrees of neighboring nodes are uncorrelated. Thus we may replace \(A_{xy}\) by \(\langle A_{xy}\rangle = k_xk_y/\mu_1N\) in (11). Following the same steps as in the complete bipartite network, the backward Kolmogorov equation for the consensus time is \begin{equation} \label{VM:Kol-t} \sum_k v_k \frac{\partial T}{\partial\rho_k} + \sum_k D_k \frac{\partial^2 T}{\partial\rho_k^2} =-1, \end{equation} with degree-dependent velocity and diffusivity (\(v_k,D_k)\).
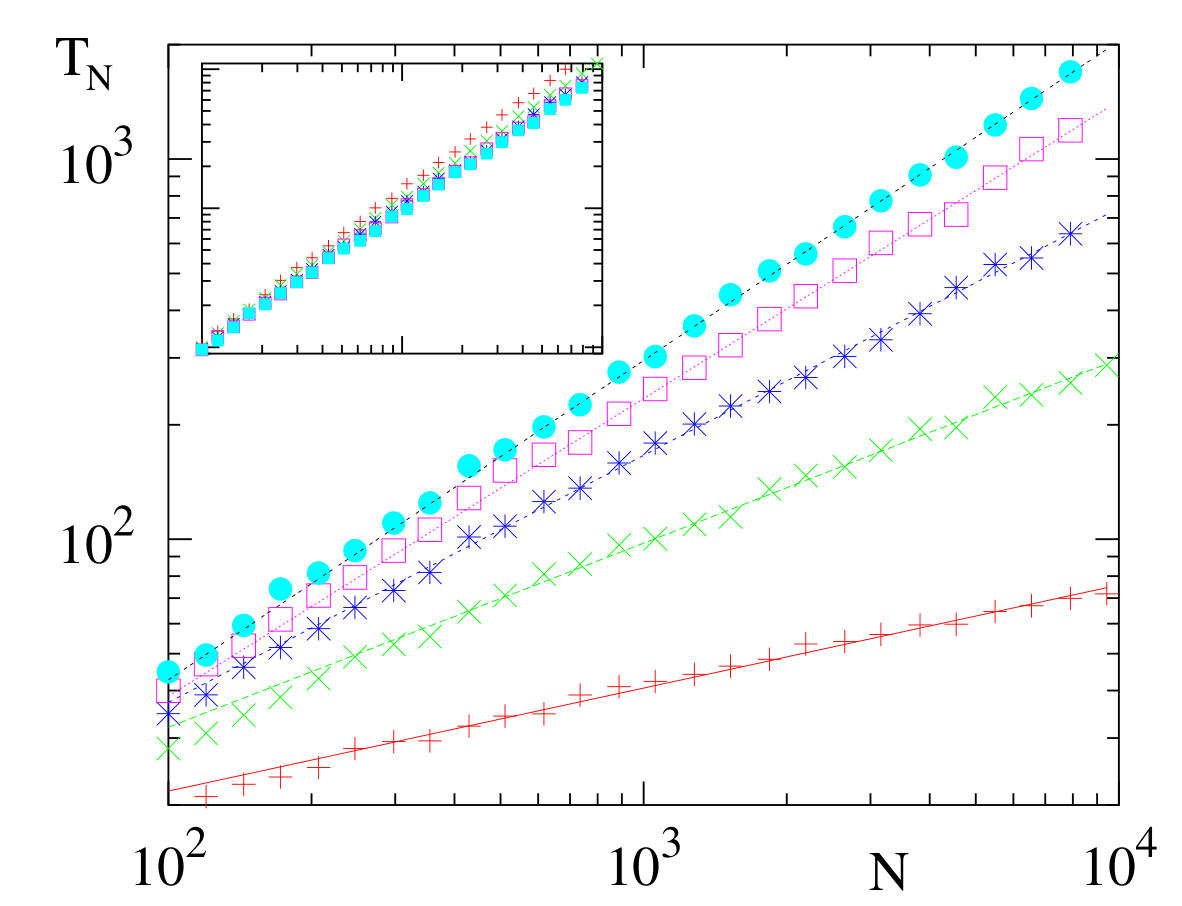
Figure 4. Consensus time \(T_N\) versus \(N\) for the configuration model with degree distribution \(n_k = k^{-\nu}\) for \(\nu = 2.1\) \((+)\), \(2.3\) \((\times)\), \(2.5\) \((\ast)\), \(2.7\) \((\circ)\) and \(2.9\) \((\bullet)\). Data are based on 100 graph realizations and 10 realizations of VM dynamics on each graph. Lines represent the prediction (15). The inset shows the same data plotted in the scaled form \(\mu_2T_N/\mu_1^2\) versus \(N\).
To simplify (12), it is helpful to first study the time dependence of the density of voters in state \(\mathbf{1}\) on nodes of fixed degree \(k\). As seen in Fig. 3(b) (and can be shown analytically), the average densities \(\langle \rho_k\rangle\) all converge to the common value \(\omega\) in a time of the order of 1. Thus, at long times, \(v_k\) in (12) vanishes. We also convert derivatives with respect to \(\rho_k\) to derivatives with respect to \(\omega\) by \(\frac{\partial T}{\partial\rho_k}=\frac{\partial T}{\partial\omega} \frac{\partial\omega}{\partial\rho_k} = \frac{k n_k}{\mu_1}\frac{\partial T}{\partial\omega}\,,\) to reduce (12) to \begin{equation} \label{VM:HG:BPE} \frac{\mu_2}{N\mu_1^2}\, \omega(1-\omega)\, \frac{\partial^2 T}{\partial \omega^2} =-1. \end{equation} Defining an effective population size by \(N_{\mathrm{eff}} = N\,{\mu_1^2}/{\mu_2}\), and comparing with (9), the consensus time is \begin{equation} \label{TVM} T_N(\omega)= -N_{\rm eff} \left[(1-\omega)\ln(1-\omega) + \omega \ln\omega\right] ~. \end{equation} This is the same form as on the complete graph and the complete bipartite network, expect for the value of \(N_{\rm eff}\). To compute \(N_{\rm eff}\) for a network with a power-law degree distribution, \(n_k \sim k^{-\nu}\), is a standard exercise in extreme-value statistics [7], and the final result is
\begin{equation} \label{VM:HG:SF:CT} T_N \propto N_{\rm eff} \sim \begin{cases} N & \nu>3,\\N^{2(\nu-2)/(\nu-1)} & 2<\nu<3,\\{\cal O}(1)& \nu<2, \end{cases} \end{equation} with logarithmic corrections in the marginal cases of \(\nu=2,3\). For \(\nu< 3\), consensus arises quickly because \(N_{\rm eff}\) is much less than \(N\) when the degree distribution is sufficiently broad. Here, a few of high-degree nodes "control'' many neighboring low-degree nodes, so the effective number of independent voters is less than \(N\).
Applying this same formalism to the IP, the consensus time is \begin{equation} \label{TIP} T_N(\omega_{-1})= -N_{\rm eff} \left[(1\!-\!\omega_{-1})\ln(1\!-\!\omega_{-1}) \!+\! \omega_{-1} \ln\omega_{-1}\right]\,. \end{equation} with \(N_{\rm eff}=N\mu_1\mu_{-1}\). For power-law degree networks, \(\mu_1\) and \(\mu_{-1}\) can be straightforwardly obtained to give \begin{equation} \label{T:IP} T_N \propto N_{\rm eff} \sim \begin{cases} N & \nu>2,\\N^{3-\nu} & \nu<2, \end{cases} \end{equation} with again a logarithmic correction for the marginal case \(\nu=2\). Thus, the consensus time in the IP is linear in \(N\) for \(\nu>2\) and superlinear in \(N\) for \(\mu<2\). Consensus arises slowly because of the difficulty in changing the opinions of agents on the very many low-degree nodes.
What happens when the two states are inequivalent? We may view state as a mutant with fitness that invades a population of “residents” in state , each of which has fitness . What is the fixation probability, namely, the probability that a single fitter mutant overspreads the population? Such fixation underlies many social and epidemiological phenomena (see e.g., [8, 9, 10, 11, 12, 13, 14]).
We implement biased dynamics for the VM as follows:
Thus, a “weaker” voter is more likely to be picked and be influenced by a neighbor. We may equivalently view the inverse fitness as the death rate for a given voter. Similarly, the evolution steps in the biased IP are
A fitter mutant is thus more likely to spread its progeny.
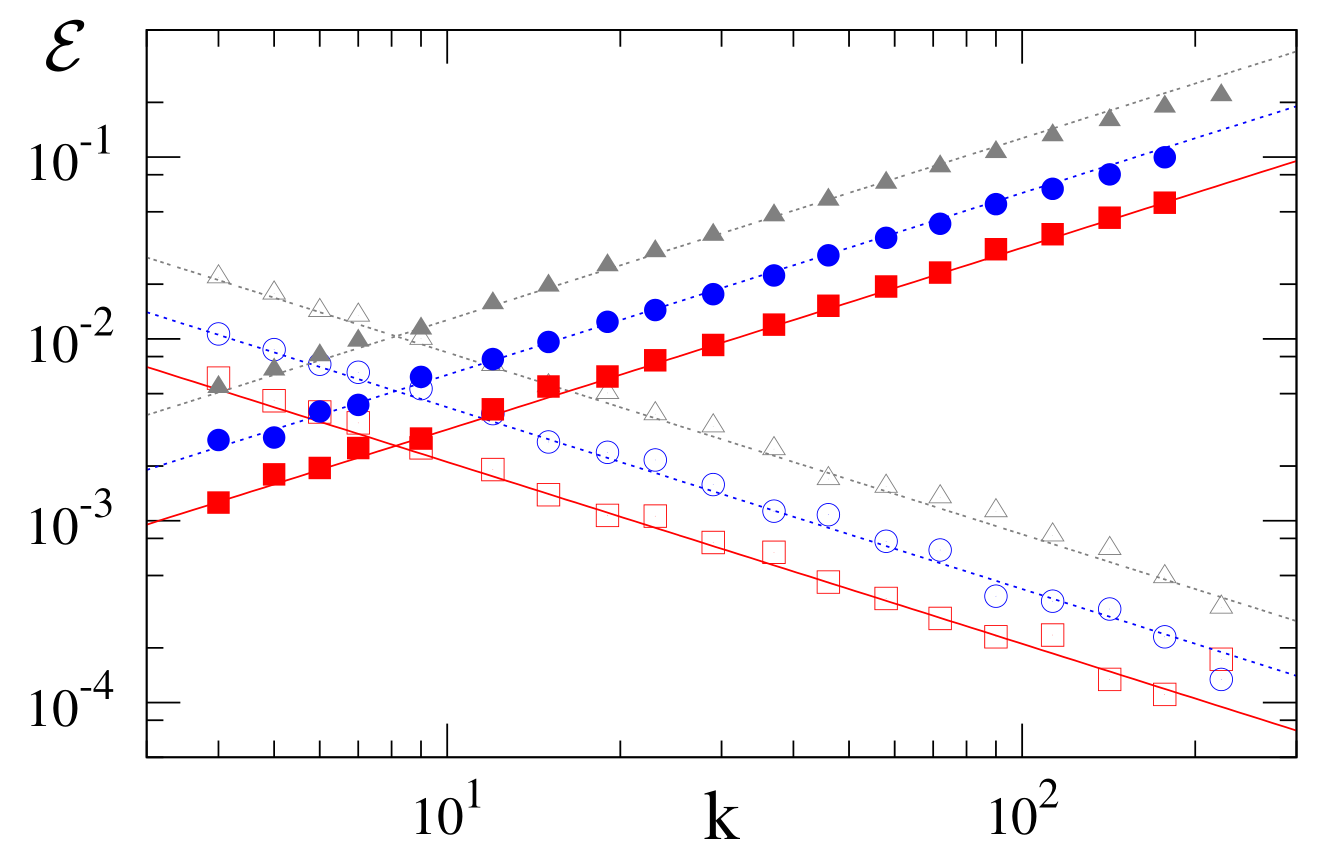
In unbiased dynamics, we saw that high-degree nodes strongly influence the fixation probability in the VM, while low-degree nodes are more influential in the IP. This trend is confirmed by Figure 5, where the fixation probability is proportional to the degree of the mutant node in the VM and proportional to the inverse of this degree in the IP.
To understand the fixation probability, let’s again consider the simple example of the complete graph. The raising and lowering operators in Eq. (5) now are
We now write the backward Kolmogorov equation for , the fixation probability to reach consensus when the initial density of agents in state equals :
subject to the boundary conditions and . In analogy with Eq. (6), this equation expresses the fixation probability as the appropriately weighted average of the fixation probabilities after a single update step. In the following, we focus on the weak selection limit, in which , with . Expanding (18) to second order in gives \begin{equation} \label{VM:bVM:RG:KBG} \rho(1-\rho) \left[s \frac{\partial\mathcal{E}}{\partial \rho} +\frac{1}{N} \frac{\partial^2\mathcal{E}}{\partial \rho^2} \right]=0\,. \end{equation} This coincides with the equation for the fixation probability to \(\rho=1\) for biased diffusion on the finite interval \([0,1]\), with solution [5, 11] \begin{equation} \label{bLDsolcont} \mathcal{E}(\rho;sN)\simeq \frac{1-e^{-sN\rho}}{1-e^{-sN}}\,. \end{equation} Here, we explicitly write the dependence of the fixation probability on \(\rho\) as well as on a second natural variable combination \(sN\).
To obtain the fixation probability on a complex network, we extend the two time-scale dynamics of the unbiased VM to biased dynamics. Here the population is again quickly driven to a homogeneous state where for all on a time scale of the order of 1. Once this homogeneous state is reached, the new feature is that consensus is driven by the bias, rather than by diffusive fluctuations. Thus, we are led to study the evolution of , which, for , evolves as . This gives on a time scale of the order of .
We now determine the fixation probability by applying the same computational approach as that for the unbiased VM: replace by in all transition probabilities and the derivative by . With these replacements, the backward Kolmogorov equation for the fixation probability has the same form as Eq. (19), but with replaced by and by . The fixation probability for biased dynamics on a complex network is then given by Eq. (20) with these replacements.
For a single mutant initially at a node of degree , . Substituting this into (20), we find generally that the fixation probability is proportional to for all and has the limiting behaviors (Figure 5): \begin{equation} \label{VM:bVM:fix:k:sol} \mathcal{E} \simeq \begin{cases} {\displaystyle k/N\mu_1} & \quad s \ll 1/N_{\mathrm{eff}} ;\\ {\displaystyle k\, (s \mu_1/\mu_2)} & \quad 1/N_{\mathrm{eff}} \ll s \ll 1. \end{cases} \tag{21}\end{equation}
In the complementary biased IP, the fixation probability for a mutant initially on a node of degree is inversely proportional to the node degree:\begin{equation} \label{VM:bIP:fix:k:sol} \mathcal{E} \simeq \begin{cases} {\displaystyle k^{-1} /N\mu_{-1}} &\quad s\ll 1/N ;\\ {\displaystyle k^{-1}(s/\mu_{-1})} &\quad 1/N\ll s\ll 1\,. \end{cases} \tag{22} \end{equation}
The venerable voter model played a central role in probability theory and statistical physics because it is one of the few exactly soluble many-particle interacting systems in all spatial dimensions and because of the diversity of its applications. Putting the voter model on a complex network—in which there is broad distribution of node degrees—changes its dynamics in crucial ways.
A new dynamical conservation law—the degree-weighted magnetization—gives the fixation probability for the voter model and the invasion process on finite networks. Another new feature is a two time-scale approach to consensus—first an initial quick approach to a homogeneous state in which the density of s is the same for nodes of any degree, after which diffusive fluctuations drive the consensus. Consensus is achieved quickly in the voter model when the degree distribution is sufficiently broad, as high-degree nodes effectively “control” many neighboring low-degree nodes. When one state is more fit, there is again a two time-scale approach to consensus, but with fitness selection driving ultimate consensus. As a message for evolutionary dynamics, for a mutant to infiltrate a network most effectively, it is advantageous for it to be on a high-degree node in the voter model and on a low-degree node in the invasion process.
[1] V. Sood and S. Redner, Phys. Rev. Lett. 94, 178701 (2005); T. Antal, S. Redner, and V. Sood, Phys. Rev. Lett. 96, 188104 (2006); V. Sood, T. Antal, and S. Redner, Phys. Rev. E 77, 041121 (2008).
[2] T. M. Liggett, Interacting Particle Systems, (Springer-Verlag, Berlin, 2005).
[3] P. L. Krapivsky, Phys. Rev. A 45, 1067 (1992).
[4] N. G. van Kampen, Stochastic Processes in Physics and Chemistry, 2nd ed. (North-Holland, Amsterdam, 1997).
[5] S. Redner, A Guide to First-Passage Processes, (Cambridge University Press, New York, 2001).
[6] M. E. J. Newman, Networks: An Introduction (Oxford University Press, 2010).
[7] J. Galambos, The Asymptotic Theory of Extreme Order Statistics, (R. E. Krieger Publishing Co., Malabar, Florida, 1987).
[8] P. A. P Moran, The Statistical Processes of Evolutionary Theory (Clarendon Press, Oxford, 1962).
[9] M. Kimura, The Neutral Theory of Molecular Evolution, (Cambridge University Press, Cambridge, 1983).
[10] R. M. Anderson and R. M. May, Infectious Diseases in Humans, (Oxford University Press, Oxford, 1992).
[11] W. Ewens, Mathematical Population Genetics I. Theoretical Introduction, (Springer-Verlag, Berlin, 2004).
[12] M. A. Nowak, Evolutionary Dynamics, (Harvard Univ. Press, Cambridge MA 2006).
[13] R. Pastor-Satorras and A. Vespignani, Phys. Rev. Lett. 86, 3200 (2001).
[14] D. J. Watts, Proc. Natl. Acad. Sci. USA 99, 5766 (2002).