Editor's note: This article originally appeared in the SIAM News (vol. 42, no. 10, Dec. 2009). We reprint it here with permission of SIAM News and the author.
An old rap against biologists is that they chose a science as far from mathematics as they could get -- only to wake up in an age of computer models and bioinformatics. Following a similar path of least resistance, stereotypical applied mathematicians steered clear of a subject called topology; to the extent that this is so, they could be in for a similar slow but rude awakening. In an invited presentation on sensor networks and topology at this year's SIAM Conference on Applications of Dynamical Systems, Robert Ghrist of the University of Pennsylvania showed how the softer side of geometry is infiltrating the analysis of complex systems.
In particular, Ghrist predicts that coming generations of applied mathematicians and other computational scientists and engineers will embrace a term now rarely uttered outside esoteric academic specialties: homology.
It's happened before, Ghrist points out. In the 1960s, differentiable manifolds were primarily the purview of pure theorists. By the 1980s, applied mathematicians were writing books on manifolds, stable and unstable. Nowadays, it's often engineers who wax eloquent on the nature of hetero- and homoclinic points. It's hard to escape an idea whose time has come.
Broadly speaking, homology is a mathematical mechanism for collating individually meaningless, local data into useful, global information. A famous example concerns triangulated surfaces: If each vertex of a triangulation (of a compact surface without boundary, to be precise) reports its "degree" -- the number of edges emanating from it -- then the number of vertices V and the total degree D can be combined into the interesting number V - D/6, which turns out to depend only on the surface, and not the specific triangulation. This number, known as the Euler characteristic, relates to the number of "holes" in the surface. (The formula for the Euler characteristic is more generally given as V - E + F, where E and F are the numbers of edges and faces when the surface is cut into bite-sized chunks, not necessarily triangles. When all chunks are triangles, E = D/2 and F = D/3.)
Collecting local data is what sensors do -- even a telescope registers only the photons that enter its aperture. Sensors have become ubiquitous: You can't go into a public restroom in most places without the faucets, hand driers, and toilets taking note of your presence. Increasingly, sensors are networked, so that the left hand might know what the right hand is doing. And that's where things become potentially topological.
The standard engineering paradigm of sensor technology envisions more or less complete and exact knowledge of the locations of sensors and the data streams they are built to provide, with all this information centrally processed and controlled. Indeed, for certain sensor systems -- say the traffic-detector loops put in place to coordinate rush-hour gridlock -- such centralized planning makes sense. But this assumes essentially unlimited communications and computing power. What happens when sensors are constrained by cost or uncertainty?
Overlapping scraps of data can be stitched together to form a crazy quilt of insight. Take, for example, a network of randomly placed sensors, each able to identify any fellow sensors within some reasonable radius of its (unknown) position and to count the number of other nearby objects of interest, generically known as "targets." Ghrist and colleagues have shown how tools of topology, including souped up versions of the Euler characteristic, can answer a variety of such questions: Does the network cover the entire domain of interest? Are there obstacles, such as walls, that limit some sensors' view? How many "targets" are there altogether?
The technical answers depend, of course, on additional technical assumptions. In a 2006 paper that appeared in the International Journal of Robotics Research, Ghrist and Vin de Silva of Pomona College considered the coverage problem for polygonal domains in \(\mathbb{R}^2\), with one set of "fencepost" sensors at the vertices of the polygon and another batch scattered about the interior. Their main result is that complete coverage of the domain can be verified by finding a certain nontrivial homology class. One useful corollary has to do with cost-cutting: Once you compute which sensors correspond to the crucial homology class, you can turn off or ignore the others. Alternatively, if you compute more than one representative of such a class, you've got yourself a fault-tolerant backup system. (See illustration.)
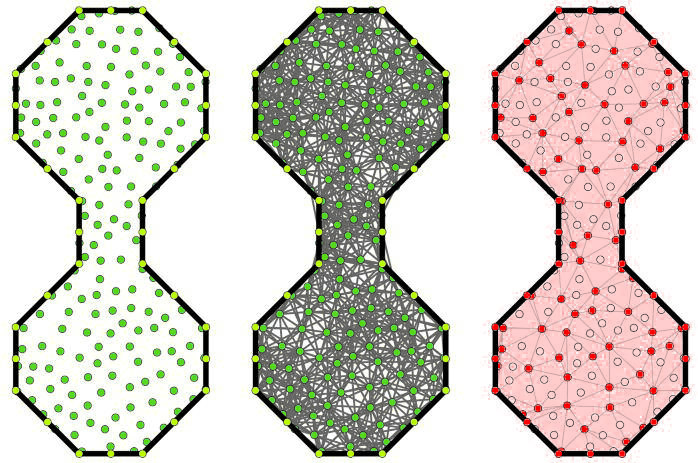
Sleep Mode. When sensors are scattered about a region (left), a homology computation can determine whether they provide complete coverage simply from knowledge of which sensors are within each other's sensing radius (center). The homology computation also suggests sensors that can be turned off without loss of coverage (right). From V. de Silva and R. Ghrist, "Coordinate-free Coverage in Sensor Networks with Controlled Boundaries via Homology," International Journal of Robotics Research, Vol. 25, No.12, 2006, pages 1205-22.
But how computable are such things? Topology has a reputation for being abstract. Indeed, the theory has a tendency to wander off into a thicket of sub- and superscripted notation, intricate terminology, and formulas that fill the better part of a blackboard. But linear programming, and linear algebra generally, have the same tendency. In fact, the whole point of algebraic topology is to provide an algebraic toolbox for objects whose plastic nature seemingly defies any effort to pin them down.
Homology groups in particular are eminently computable. As a postdoc with the computational topology group at Stanford University in the early 2000s, de Silva developed Plex, a suite of MATLAB routines for studying simplicial complexes, which, in rough algebraic-topology-speak, are networks. (The simplest kind of simplex is a clique within a graph, e.g., a tight grouping of sensors, each aware of the others' existence.) Plex, now in its third (Java) version, is available at the Stanford computational topology group's website, comptop.stanford.edu.
The extensive machinery of algebraic topology is giving computational scientists plenty of new tools to work with, Ghrist says. It has also kept them busy reading the instruction manuals. Applying homology is just step one. Wait until you get to the part on applied sheaf theory.
Barry A. Cipra is a mathematician and writer based in Northfield, Minnesota.