Anastasia Bizyaeva, based on work done in collaboration with Alessio Franci and Naomi Ehrich Leonard.

Emergent properties of complex social systems are shaped by the beliefs of individuals that compose them. People embedded in online and offline social networks form beliefs on political topics that inform their day-to-day actions, determine the outcomes of elections, and contribute to echo chamber formation and extremism. Animals evaluate the quality of candidate nest sites, foraging patches, and movement directions to make consensus decisions. Technological agents in robotic teams, autonomous vehicle networks, and mobile sensor networks also leverage communication and sensing to form beliefs, for example on which action to take or which direction to move to accomplish a design objective.

Mathematical models of belief formation dynamics are useful analogies for the study of real-world social systems [1] and a tool for the design of collective behavior in engineered teams [2]. A belief of an individual, or agent, \(i\) about option or topic \(j\) is modeled with a scalar variable \(z_{ij} \in \mathbb{R}\). Whether an agent favors, disfavors, or has no opinion on a particular option is captured by the sign and magnitude of its corresponding belief (some models also consider beliefs constrained to a simplex, or beliefs that belong to a discrete set). A model of belief formation describes how agents update their beliefs over time in response to complex interplays of social, cognitive, and environmental factors.

Recently, a novel agent-based model of belief dynamics was developed in [3, 4, 5, 2]. In this model, agents' beliefs evolve in continuous time according to a nonlinear update rule that synthesizes the influence of social networks and of several internal driving factors within agents' cognition. The model's nonlinearity sets it apart from traditional linear models [6, 7, 8], and is well-grounded for modeling complex systems with emergent decision-making based on ideas from cognitive science, signal processing, and collective animal behavior, as discussed in [9, 4, 2]. In this article, we summarize key ideas behind the formulation of the model and several insights about belief formation that are gained from its analysis.

Two graphs

A key ingredient in any social network model is the communication graph \(\mathcal{G}_a = (\mathcal{V}_a,\mathcal{E}_a,s_a)\) that encodes the structure and nature of social relationships. The set of vertices \(\mathcal{V}_a\) represents the \(N_a\) agents in the group. Whenever the edge \(e_{ik} \in \mathcal{E}_a\), agent \(i\) receives information about the beliefs of agent \(k\) through some form of communication, sensing, or estimation. The edge signature \(s_a: \mathcal{E}_a \to \{1,-1\}\) classifies the relationships between agents; whenever \(s(e_{ik}) = 1\), agent \(i\) sees agent \(k\) as a friend or teammate, whereas \(s(e_{ik}) = -1\) signifies an antagonistic relationship. The communication graph is associated with a signed, and possibly weighted, adjacency matrix \(A_a \in \mathbb{R}^{N_a \times N_a}\).

The communication graph and its adjacency matrix play a key role in virtually any agent-based model of collective behavior, including models of belief dynamics. However, it is not the only graph that matters. Literature in belief dynamics modeling is beginning to embrace that realistically, beliefs on different topics do not evolve in an ideological vacuum and can be interdependent due to various logical, social, and psychological constraints [10, 11, 12, 13]. Such constraints constitute an individual's belief system [14] and can be formalized mathematically as a belief system graph \(\mathcal{G}_o = (\mathcal{V}_o, \mathcal{E}_o, s_o)\). The vertices in the set \(\mathcal{V}_o\) are the \(N_o\) options or topics, and the edges \(e_{jl} \in \mathcal{E}_o\) and their signature \(s_o(e_{ij}) \in \{1,-1\}\) encode the interdependencies between different topics. Belief system graphs provide an additional structure that, together with the social network structure, constrains how beliefs in a group can evolve.

A common example of a belief system is the left-right spectrum of political ideology. Two beliefs on the same "side" of this spectrum, such as beliefs about the need for universal healthcare and for environmental regulations, would be connected by a positive edge on the belief system graph, indicating correlation or alignment. Conversely, two beliefs that are opposed on this spectrum, such as one about the need for universal healthcare and one on heightening immigration control policies, would be connected by a negative edge, indicating anti-correlation or misalignment. Belief system graphs can exhibit more complex structure, especially when multiple ideological dimensions are necessary to classify different belief alignments. Furthermore, belief systems can be defined globally for all agents or separately for each individual. The former might correspond to a society that promotes a unified ideological narrative, while the latter may be the case in a society that is more ideologically diverse. A belief system graph is also associated with a signed, and possibly weighted adjacency matrix \(A_o \in \mathbb{R}^{N_o \times N_o}\).

Four social forces and Networks of Beliefs Theory

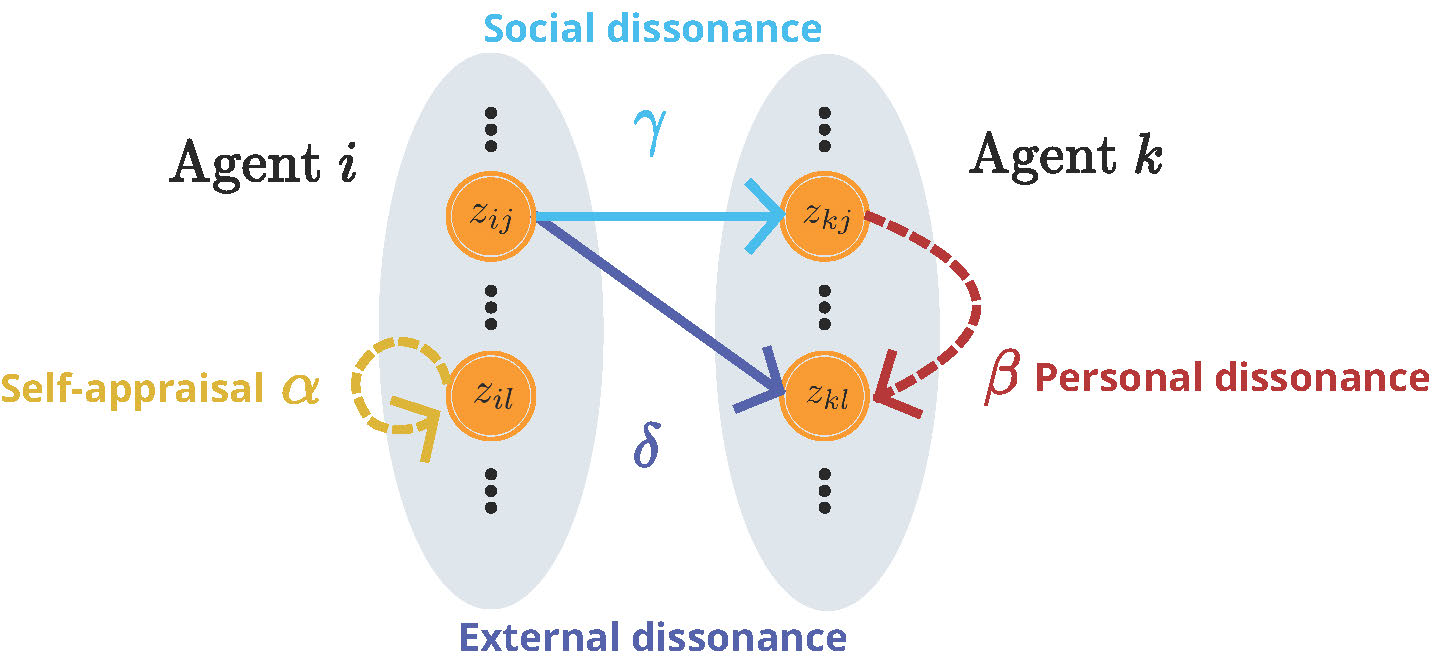
Figure 1: Four representative coupling arrows that represent the four social forces that influence belief formation according to (1). Social gains \(\alpha, \beta, \gamma, \delta \geq 0\) modulate the amount of attention allocated to each of the four effects. Figure is adapted from [5].

The belief dynamics model of [5] incorporates into a nonlinear dynamical system several key ideas from Networks of Beliefs Theory, a recent framework proposed in social psychology for modeling belief formation in social networks [13]. Some of these premises include:

1. Modeling belief dynamics requires a "networks of networks" perspective, wherein beliefs interact on an internal network within an individual's cognition (e.g. one constrained by belief system structure) as well as on an external network between individuals (e.g. a social network).

2. Various internal and external misalignments between agents' own beliefs and those of their social neighbors lead to the experience of cognitive dissonance. Beliefs of individuals are dynamically updated to minimize and therefore resolve this dissonance.

Following these ideas, belief formation in [5] is modeled as a dissonance minimization, where cognitive dissonance arises from several of the sources proposed by [13]. Personal dissonance arises from the internal conflict one experiences when holding contradictory beliefs. Social dissonance arises when an individual's beliefs are at odds with the perceived beliefs of their social circle, i.e. it is a social pressure to align one's own beliefs better with those of one's in-group and anti-align them with one's out-group. External dissonance occurs when an individual's belief on a specific topic conflicts with their perception of what their social circle believes about other, related topics. In addition to these three effects, the model accounts for a self-appraisal of beliefs, i.e. a self-confidence of agents that counterbalances their experience of dissonance. These four social forces are associated with four distinct types of coupling arrows between the belief vectors of neighboring individuals, pictured in Figure 1. Different amounts of attention can be allocated by agents to each of the four social forces, which we associate with nonnegative parameters \(\beta, \gamma, \delta, \alpha\) in the listed order of social forces.

Dynamic belief updates follow the structure \(\dot{z}_{ij} = - (z_{ij} - D_{ij}(\mathbf{Z}) - b_{ij})\) where \(D_{ij}\) is the contribution to the cognitive dissonance from the four outlined social forces on option \(j\) and \(b_{ij}\) is a pre-existing bias of the agent. At steady-state, for every agent \(i\) and option \(j\), \(z_{ij} = D_{ij}(\mathbf{Z}) + b_{ij}\) which corresponds to zero dissonance. For a social network of homogeneous (but possibly biased) agents with a globally defined belief system structure, the belief update model reads

\( \small \dot{z}_{ij} = \mkern-15mu \underbrace{-z_{ij}\vphantom{\sum_{\substack{l=1 \\ l \neq j}}^{N_o} \sum_{\substack{k=1 \\ k \neq i}}^{N_a}}}_{\text{resistance}} \mkern-15mu + \ u S\bigg( \underbrace{\alpha (A_a)_{ii} (A_o)_{jj} z_{ij}\vphantom{\sum_{\substack{l=1 \\ l \neq j}}^{N_o} \sum_{\substack{k=1 \\ k \neq i}}^{N_a}}}_{\text{self-appraisal}} + \underbrace{\beta \sum_{\substack{l=1 \\ l \neq j}}^{N_o} (A_{a})_{ii} (A_o)_{jl} z_{il}}_{\text{personal dissonance}} + \underbrace{\gamma \sum_{k=1}^{N_a}(A_a)_{ik} (A_o)_{jj} z_{kj}\vphantom{\sum_{\substack{l=1 \\ l \neq j}}^{N_o} \sum_{\substack{k=1 \\ k \neq i}}^{N_a}}}_{\text{social dissonance}} + \underbrace{\delta \sum_{\substack{l=1 \\ l \neq j}}^{N_o} \sum_{\substack{k=1 \\ k \neq i}}^{N_a} (A_a)_{ik}(A_o)_{jl} z_{kl}}_{\text{external dissonance}} \bigg) + \underbrace{b_{ij}\vphantom{\sum_{\substack{l=1 \\ l \neq j}}^{N_o} \sum_{\substack{k=1 \\ k \neq i}}^{N_a}}}_{\text{bias}}. \)

(1)

In (1), the first term is a resistance to forming strong beliefs, andd \(S\) is a saturating nonlinearity satisfying \(S(0) = 0\), \(S'(0) = 1\). This nonlinearity introduces a layer of nonlinear processing of social information and reflects the fact that dissonance effects are bounded. The parameters \(\alpha,\beta,\gamma,\delta\) are relative amounts of attention to each of the the four social forces, as pictured in Figure 1, and \(u \geq 0\) is the absolute amount of attention to all of the social effects. In the analysis of (1) in [5], the absolute attention parameter \(u\) serves as a bifurcation parameter, although the relative attention parameters \(\alpha,\beta,\gamma,\delta\) can equivalently be utilized in this way.

Belief formation as an indecision-breaking bifurcation

A key prediction of (1) is that strong beliefs emerge in a group when agents pay enough attention to their cognitive dissonance. When the overall attention \(u\) is low, agents' beliefs track their biases \(b_{ij}\). However, at a critical attention threshold \(u = u^*\), nonlinear dissonance effects dominate and strong beliefs form. After this critical point, the pattern of beliefs in a group is primarily determined not by the agents' biases, but by the structure of the social network and belief system graphs. Formally, (1) is a coupled cell system and formation of strong beliefs is the consequence of a bifurcation. Analysis of (1) relies on tools from network bifurcation theory [15, 4].

When agents are unbiased, the state \(\mathbf{Z} = \mathbf{0}\) is an equilibrium of (1). This steady-state configuration of beliefs corresponds to global neutrality or indecision in the group, meaning all agents refrain from taking on any affirmative or negative stances on issues they are evaluating. The Jacobian matrix of the linearization of (1) at the indecision eqiulibrium decouples into the effects of the four social forces,

\( J (\mathbf{0},u) = \underbrace{(- 1 + u \alpha) \mathcal{I}_{N_a}\otimes \mathcal{I}_{N_o}}_{\text{resistance and self-appraisal}} + \underbrace{u \beta \mathcal{I}_{N_a} \otimes \hat{A}_o}_{\text{personal dissonance}} + \underbrace{u \gamma \hat{A}_a \otimes \mathcal{I}_{N_o}}_{\text{social dissonance}} + \underbrace{u \delta \hat{A}_a \otimes \hat{A}_o}_{\text{external dissonance}}, \)

(2)

where \(\otimes\) is the Kronecker product of matrices, \((A_o)_{jj} = 1\) for all \(j\), \((A_a)_{ii} = 1\) for all \(i\), \(\hat{A}_a = A_a - \mathcal{I}_a\), and \(\hat{A}_o = A_o - \mathcal{I}_o\). Analysis in [5] leads to the following theoretical insights, informed by the structure of (2):

1. Global indecision is stable when \(u < u^*\), and unstable when \(u > u^*\). Belief formation from any initial condition on the network tends towards global neutrality over time when agents pay little attention to their cognitive dissonance.

2. The critical attention threshold \(u^*\) is tuned by the relative attention to the four social forces and by the structure of \(\mathcal{G}_a\), \(\mathcal{G}_o\). Global indecision loses stability when the attention reaches

\( u^* = \frac{1}{\alpha + \gamma \operatorname{Re}(\lambda_a) + \beta \operatorname{Re}(\mu_o) + \delta \operatorname{Re}(\lambda_a \mu_o)} \)

(3)

where \(\lambda_a\) is an eigenvalue of \(\hat{A}_a\) and \(\mu_o\) is an eigenvalue of \(\hat{A}_o\) satisfying

\( (\lambda_a,\mu_o) = \operatorname{argmax}_{\lambda \in \sigma(\hat{A}_a),\ \mu \in \sigma(\hat{A}_o)}( \gamma \operatorname{Re}(\lambda) + \beta \operatorname{Re}(\mu) + \delta \operatorname{Re}(\lambda \mu)). \)

(4)

Whenever relative attention to one of the four social effects increases, the bifurcation threshold decreases and agents are more prone to forming strong beliefs.

3. Belief patterns away from neutrality are informed by the structure of \(\mathcal{G}_a\), \(\mathcal{G}_o\). Non-neutral beliefs arise from a bifurcation at \(u = u^*\) along a center manifold of the origin. The structure of the center manifold, due to the structure of (2), is approximated to first-order by a right eigenspace of the graph product adjacency matrix \(\hat{A}_a \otimes \hat{A}_o\). The pattern of beliefs that emerge on this manifold is therefore constrained to be near this dominant eigenspace, which we refer to as the critical subspace, especially when the absolute attention \(u\) is near its bifurcation threshold.

A typical indecision-breaking bifurcation in (1) is pictured in Figure 2. Whenever the two eigenvalues \(\lambda_a, \mu_o\) satisfying (4) are both simple and real, with corresponding right eigenvectors \(\mathbf{v}_a, \mathbf{v}_o\) and left eigenvectors \(\mathbf{w}_a,\mathbf{w}_o\), a symmetric pitchfork bifurcation is the organizing center for the bifurcation diagram of (1) near \(u = u^*\), \(\mathbf{Z} = \mathbf{0}\). We will call an equilibrium at which some or all of the agents form at least one nonzero belief a decision state for the network.

In a group of unbiased agents, two simultaneously stable decision states appear near the critical space \(\operatorname{span}(\mathbf{v}_a \otimes \mathbf{v}_o)\) (Figure 2, left). In this case, the left eigenspace \(\operatorname{span}(\mathbf{w}_a \otimes \mathbf{w}_o)\) is the sensitivity subspace that determines how biases affect the belief formation outcome. Near \(u = u^*\), the belief formation dynamics amplify arbitrarily small biases along the sensitivity subspace. Specifically, the projection of network bias vector \(\mathbf{b}\) onto the sensitivity subspace predicts whether the bistability between the two decision states is broken near the critical attention threshold. When the bistability is broken, the decision state that is misaligned with the agents' biases is no longer viable for the group, and the "correct" decision state is the only remaining equilibrium (Figure 2, right).

Sensitivity of a social decision to bias and external information is further amplified when attention of agents is allowed to vary over time. For example, slowly increasing the attention parameter \(u\) from below its critical threshold \(u^*\) to a supercritical value results in a drift along the bifurcation diagram of Figure 2. The beliefs of unbiased agents will eventually converge towards one of the two bistable decision states, with the choice determined entirely by the distribution of initial conditions. In contrast, the beliefs in a group of biased agents will follow the decision state selected by their biases and the sensitivity subspace, roughly tracking the continuous branch of solutions pictured in the right-side diagram of Figure 2. Beyond slow parameter drift, agents may update their attention reactively in response to the beliefs others in their social circle. Such dynamic state feedback can give rise to flexible transitions from a global state of indecision to a decision state, and between different decision states when biases change. We explore this coupling between belief formation and attention dynamics, as well as their relevance for the design of social decision algorithms in [16, 17, 2].

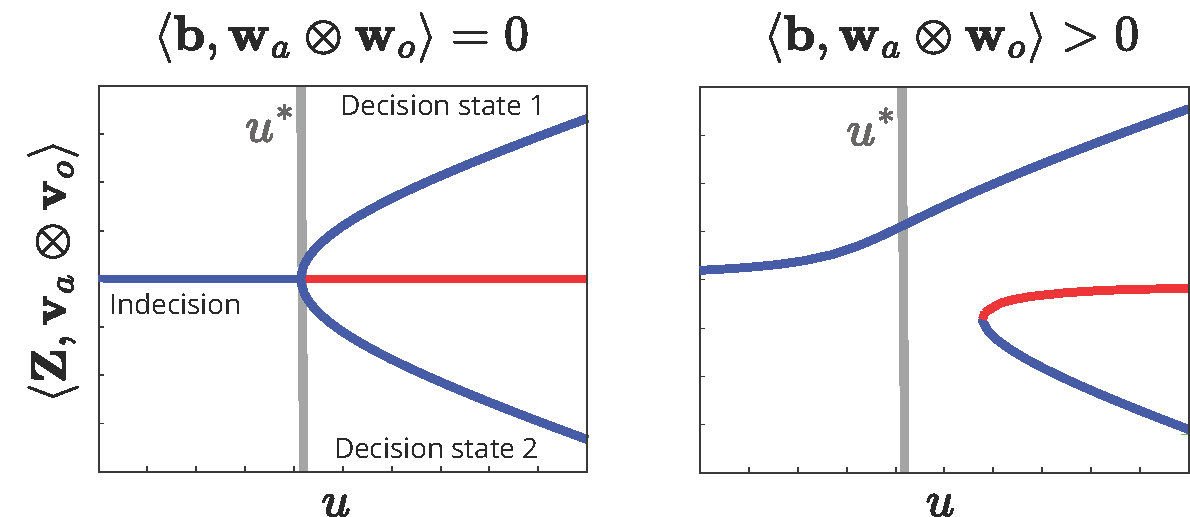
Figure 2: Representative bifurcation diagram of (1) for an unbiased (left) and biased (right) group of agents. Blue lines are stable equilibria, and red lines are unstable equilibria. The vectors \(\mathbf{v}_a \otimes \mathbf{v}_o\) and \(\mathbf{w}_a \otimes \mathbf{w}_o\) are right and left leading eigenvectors of (2). Belief formation in unbiased network is organized through a pitchfork bifurcation, that unfolds to favor one of the decision states when biases are introduced. Figure is adapted from [3].

In Figure 3 we show a representative simulation to illustrate the relationship between the critical subspace of the pitchfork bifurcation and the pattern of beliefs formed in the group. Specifically, Figure 3 B reveals that agents' beliefs about each option align with the sign pattern of the eigenvector \(\mathbf{v}_a\) from the adjacency matrix \(A_a\) of the communication graph. Moreover, the steady-state relative magnitudes of beliefs correspond to the eigenvector entries' relative magnitudes.

Observe that the social relationships in the communication graph shown in Figure 3 A. are highly polarized. Agents 1-4 and agents 6-10 form two mutually antagonistic subgroups, with exclusively positive relationships within each group, and exclusively negative relationships between groups. This polarization mathematically corresponds to a property called structural balance, and it is reflected in the steady-state belief pattern. Specifically, beliefs within each subgroup cluster by sign, resulting in opposing viewpoints between the two subgroups.

Figure 3 D. shows an analogous insight about the internal beliefs of agents. At steady-state, each agent's beliefs about the various options follow the sign and magnitude pattern of the eigenvector \(\mathbf{v}_o\) from the adjacency matrix \(A_o\) of the belief system graph. These beliefs are termed coherent, as they conform to the logical constraints specified in the belief system graph shown in Figure 3 C. Specifically, if the belief system indicates a positive correlation between any pair of options, the agents' beliefs for those options share the same sign at steady-state, signifying either mutual acceptance or rejection. Conversely, a negative correlation in the belief system leads to internal beliefs with opposite signs. Our work in [5] identifies various classes of belief system and communication graphs that support such maximally coherent belief formation post-bifurcation.

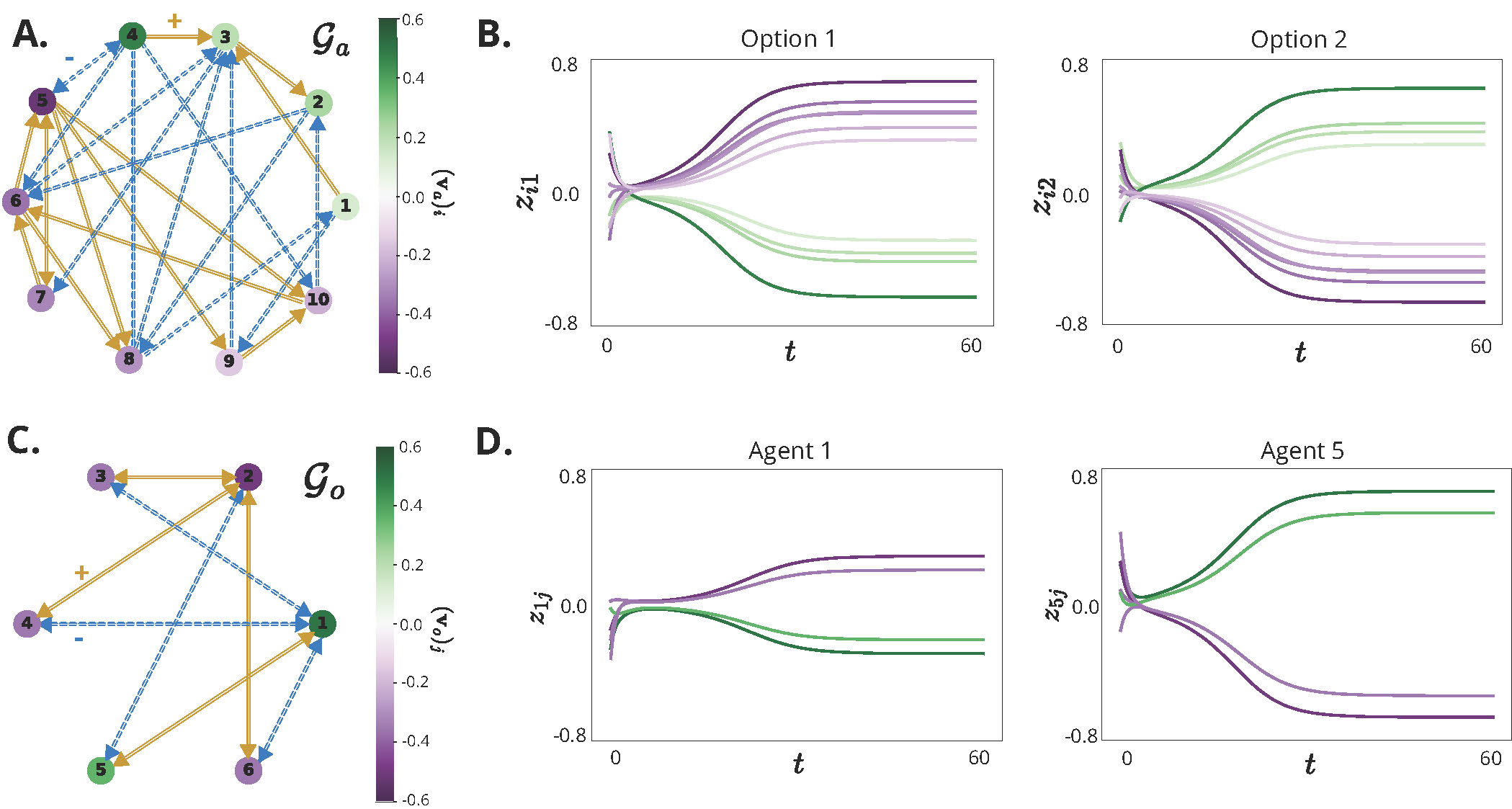
Figure 3: Simulation of (1) for 10 agents and 6 options, over communication graph pictured in A. and over belief system graph pictured in C. from a random small initial condition. Trajectories of beliefs \(z_{ij}\) of all agents about two representative options are shown in panel B., and trajectories of beliefs of two representative agents on all options are shown in panel D. Color of nodes in \(\mathcal{G}_a\), \(\mathcal{G}_o\) represents the sign and magnitude of corresponding entry in the leading eigenvectors \(\mathbf{v}_a\), \(\mathbf{v}_o\). In A., C., yellow solid lines represent positively signed edges, and blue dashed lines represent negatively signed edges. In B.,D. color of belief trajectory matches the corresponding node color in A. and C., respectively. Parameters: \(\mathbf{b} = \mathbf{0}\), \(\alpha = \beta = \gamma = \delta = 0.1\), \(u = 1\), \(S = \tanh\).

Same graphs, different beliefs: social and external dissonance-dominant bifurcations

An interesting insight from [5] is that for some graphs, different beliefs can emerge at the indecision-breaking bifurcation depending on the relative balance of social dissonance \(\gamma\) and external dissonance \(\delta\). We illustrate the transition between these two belief-forming behaviors in the following simulation. The belief system graph in the simulation is the same as in Figure 3 C., and the social network graph is pictured in the video. The simulation begins with \(\delta = 0.25\) and the beliefs of agents settle to a decision state from a random initial condition. The external dissonance parameter then increases to \(\delta = 0.3\) at \(t = 150\), and the agents' beliefs settle to a different equilibrium. This happens because the critical subspace of the pitchfork bifurcation is different for the two choices of \(\delta\). The color of nodes in the plots represents each agent's corresponding entry in the dominant social network graph eigenvector \(\mathbf{v}_a\). At steady-state, the agents' beliefs are arranged mostly in the order of their corresponding eigenvector entries. Because of this, subgroups of agents whose beliefs cluster together are different between the two scenarios. To put it simply, a change in the balance of the various dissonance effects can dramatically alter the patterns of agreement and disagreement in a group, even when the social network and belief system graph topologies, weight distributions, and sign structures are completely unchanged.

Movie 1: In the above simulation, the parameters are \(\alpha = \beta = \gamma = 0.1\), \(u = u^*+0.03\), \(S = \tanh\), and \(\mathbf{b} = \mathbf{0}\).

Final comments

In this article we summarized a novel nonlinear dynamic framework for modeling the evolution of beliefs in a social network and described several key insights from its analysis. Beyond the pitchfork bifurcation discussed here, an indecision-breaking bifurcation can give rise to oscillatory beliefs [18, 5], higher dimensional sets of simultaneously stable equilibria [4, 3], and more complicated dynamic attractors such as ergodic tori [19]. Furthermore, there are many open questions and opportunities for further analyses of this model, including understanding belief formation with heterogeneous belief systems among agents, with dynamic edge weights and graph topologies for both the belief system and the communication graphs, and away from the primary bifurcation of the origin. There are also many opportunities for application of this framework, both for modeling social behavior across different contexts and for the design of social algorithms for technological teams. For a detailed discussion of past, ongoing, and potential applications we refer the interested reader to our recent review [2].

References

[1]   Henrik Olsson and Mirta Galesic, Analogies for modeling belief dynamics, OSF Preprints, 2023.

[2]   Naomi Ehrich Leonard, Anastasia Bizyaeva, and Alessio Franci, Fast and flexible multi-agent decision-making, Annual Review of Control, Robotics, and Autonomous Systems, 2023.

[3]   Anastasia Bizyaeva, Alessio Franci, and Naomi Ehrich Leonard, Nonlinear opinion dynamics with tunable sensitivity, IEEE Transactions on Automatic Control, 68(3), pp. 1415-1430, 2022.

[4]   Alessio Franci, Martin Golubitsky, Ian Stewart, Anastasia Bizyaeva, and Naomi E. Leonard, Breaking indecision in multiagent, multioption dynamics, SIAM J. Applied Dynamical Systems}, 22(3), pp. 1780-1817, 2023.

[5]   Anastasia Bizyaeva, Alessio Franci, and Naomi Ehrich Leonard, Multi-topic belief formation through bifurcations over signed social networks, arXiv preprint arXiv:2308.02755, 2023.

[6]   R. P. Abelson, Mathematical models in social psychology, volume 3 of Advances in Experimental Social Psychology, pp. 1-54. Academic Press, 1967.

[7]   Morris H. DeGroot, Reaching a consensus, J. Am. Statistical Association, 69(345), pp. 118-121, 1974.

[8]   Noah Friedkin and Eugene Johnsen, Social influence and opinions, Journal of mathematical sociology, 15(3-4), pp. 193-206, 1990.

[9]   Alessio Franci, Martin Golubitsky, Anastasia Bizyaeva, and Naomi Ehrich Leonard, A model-independent theory of consensus and dissensus decision making, arXiv preprint arXiv:1909.05765, 2019.

[10]   Noah Friedkin, Anton Proskurnikov, Roberto Tempo, and Sergey Parsegov, Network science on belief system dynamics under logic constraints, Science, 354(6310), pp. 321-326, 2016.

[11]   Mirta Galesic, Wändi Bruine de Bruin, Jonas Dalege, Scott Feld, Frauke Kreuter, Henrik Olsson, Drazen Prelec, Daniel Stein, and Tamara van Der Does, Human social sensing is an untapped resource for computational social science, Nature, 595(7866), pp. 214-222, 2021.

[12]   Madalina Vlasceanu, Ari M. Dyckovsky, and Alin Coman, A network approach to investigate the dynamics of individual and collective beliefs: Advances and applications of the bending model, Perspectives on Psychological Science, 2023.

[13]   Jonas Dalege, Mirta Galesic, and Henrik Olsson, Networks of beliefs: An integrative theory of individual-and social-level belief dynamics, OSF Preprints, 2023.

[14]   Philip E. Converse, The nature of belief systems in mass publics (1964), Critical review, 18(1-3), pp. 1-74, 2006.

[15]   Martin Golubitsky and Ian Stewart, Dynamics and Bifurcation in Networks, SIAM, 2023.

[16]   Anastasia Bizyaeva, Timothy Sorochkin, Alessio Franci, and Naomi Ehrich Leonard, Control of agreement and disagreement cascades with distributed inputs, In IEEE Conference on Decision and Control, pp. 4994-4999, 2021.

[17]   Alessio Franci, Anastasia Bizyaeva, Shinkyu Park, and Naomi Ehrich Leonard, Analysis and control of agreement and disagreement opinion cascades, Swarm Intelligence, 15, pp. 47-82, 2021.

[18]   Anastasia Bizyaeva, Alessio Franci, and Naomi Ehrich Leonard, Sustained oscillations in multi-topic belief dynamics over signed networks, In American Control Conference, pp. 4296-4301, 2023.

[19]   Anastasia Sergeyevna Bizyaeva, Nonlinear dynamics of multi-agent multi-option belief and opinion formation, PhD thesis, Princeton University, 2022.