Research on Delayed Dynamical Systems in Budapest

by Gábor Stépán and Tamás Insperger, Budapest University of Technology and Economics

The Department of Applied Mechanics is one of the largest departments of Budapest University of Technology and Economics. The department is responsible for the basic mechanics lectures at undergraduate level in mechanical engineering, and for the advanced mechanics courses at graduate and postgraduate level for all engineering students. The teaching and research activities include the whole range of basic mechanics: from statics, dynamics, and vibrations to elasticity, plasticity, and continuum mechanics.

Staff of the Department of Applied Mechanics.

The research on delayed dynamical systems was started by Professor Gábor Stépán in the late 1970s; the first basic results are summarised in his book Retarded Dynamical Systems (Longman, 1989). Now, there are three assistant professors, two postdoctoral researchers, five PhD students and six MSc students working on delayed systems, all of them supervised by Prof. Stépán.

The milling process.

The interests of the research group are: stability analysis of delay differential equations (DDEs), bifurcation analysis of DDEs, chaotic behaviour in DDEs, analysis of DDEs with varying time delay, applications (machining processes, feedback control systems, position and force control in robotics, human and robotic balancing, shimmying wheels, wheel suspension systems). Most of the research projects come from real industrial problems. The primary research project is the dynamics of high-speed machining processes. Accurate modelling of the regenerative effect of the cutting process results in a time periodic delay-differential equation. The effect of parameter change for both linear and nonlinear cases is investigated. The aim of this research is to provide a guide on the proper choice of the feed, depth of cut and spindle speed parameters.

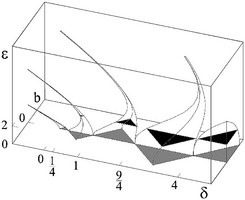
The associated basic mathematical problem is how the stability properties of the delayed Mathieu equation \(\ddot{x}(t) + (\delta + \varepsilon \mbox{cos}{t}) x(t) = x(t - 2 \pi)\) depend on its parameters. It has been proved that the stability chart of the delayed Mathieu equation is a kind of combination of the Strutt-Ince chart and the Hsu-Bhatt chart.
	Stability chart for the delayed Mathieu equation.

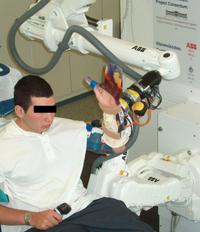
Another research area is the control of robot motions, where time delay comes from the sampling time of the digital controller and from the delay of the signals in the information transmission system. In these systems, the time delay itself is time varying as well, due to the sampling effect. Some results of this research has already been accomplished in the REHAROB Project. REHAROB is a robotic rehabilitation system for upper-limb motion therapy for the disabled. The therapy is driven by industrial robots utilising intelligent identification of the required physiotherapy motions. The teaching process of the robot is done by force control, the robot follows the path driven by the physiotherapist. During the design of the control concept, the delays and the sampling effect played an essential role in the system performance.

The robot as a physiotherapist.	Shimmy experiment on running belt.

Undesired rolling dynamics of many physical rolling systems such as aircraft nose wheels, motorcycles, automotive systems and tractor-trailer systems call the attention to the problem of shimmying wheels. The shimmy phenomenon can also be modelled by delayed dynamical systems due to the contact between the ground and the elastic tyre of the wheel that exhibits memory effects.

Test rig for demonstrating stick-slip phenomena.

In most of the above engineering problems, nonlinear analysis pointed to the possible existence of unstable periodic motion about otherwise stable equilibria and stationary motion of the systems. The corresponding subcritical Hopf bifurcations were also often identified experimentally. Stick-slip phenomena serve as nice examples of demonstrating these theoretical results by experiments. The subcritical Hopf bifurcation was shown on an accurately designed test rig.

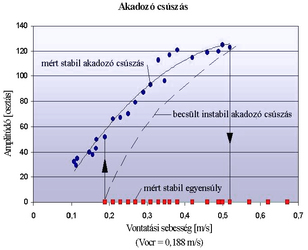Measured subcritical Hopf bifurcation (with some clarifying explanation in Hungarian)

Human balancing is also affected by time delays, namely, by the delays of our reflexes. The Delayed Dynamical Systems research group in Budapest celebrates the event of a colleague obtaining a PhD degree at a bowling club, where the mechanics subjects on rolling, sliding, friction, impact, gyroscopic effect, etc. are all studied experimentally in a relaxed atmosphere. At these occasions, the alcohol content of the consumed lager and beer is also tested by checking the critical reflex delays where small amplitude oscillations arise at the vertical position of the celebrated researchers via Hopf bifurcations. For details, see our publication lists at http://www.mm.bme.hu/.

Bowling: 3D sliding and rolling