Saksham Sharma, Pembroke College, Cambridge CB2 1RF

1. Introduction

Can the study of matter, particularly fluids - which includes, liquids, gases, gels, polymers etc. - be fundamentally described as a mathematical venture or not? Can a mathematical framework perfectly capture the dynamics of fluids or not? Are fluids inherently analytically tractable (meaning that their physics explainable by a mathematical formalism) or not? As fundamental and metaphysical these questions might sound, answers to these questions have dictated research in fluid mechanics for past many centuries. The commonly accepted belief in the community is that the fluids are composed of tiny parcels of "continuum" in which stochastic fluctuations due to atoms and molecules do not play a significant role, such that the Newton's laws of motion can be point-wise applied inside the parcel. This belief is called the "continuum hypothesis (physics)" and it has led to the derivation of almost all results in modern fluid mechanics. Yet to this date, there is no rationale for why this hypothesis works. In fact, the fluid flow suffers from major "mathematical pathologies" because of this hypothesis at first. Acknowledging the fact that the mathematical self-consistency of fluids is not well-established, this article attempts to use ideas from the discipline of "complexity sciences" to start seeing "fluids" as emergent in nature - emerging from atoms/molecules, in order to remove mathematical pathologies from the description of fluids. This article, then, presents a single abstract framework - Cantor set - to effectively solve the multi-scale physics problem of fluids, and connect arbitrary small scale physics to large scale physics in fluids; which is an attempt to present a more fundamental and complete theory of fluids. While this idea is still a theory, the article, then, concludes with the new problems and areas of research that the Cantor set framework and the complexity lens in fluids might offer to readers who are bothered by such problems.

2. Navier-Stokes regularity problem: a mathematical inconsistency in the fluid flow

The models developed to understand fluids have to be intuitive. This is because fluids exist in three dimensional spaces \(\mathcal{R}^{3}\) and thus similar to the world that we experience. However, it is possible that the scientific models we have developed are not perfect enough to describe fluids and thus, their behaviour might not be intuitive to us, or have features that are counter-intuitive. In mathematical language, these features are called "pathologies". On the other hand, if behaviour of a function does not run counter to the intuition, it is called "well-behaved". A simple example could be the distinction between general continuous and continuously differentiable functions; the latter is more well-behaved because it can be differentiated a larger number of times. In the study of fluids, it has been found that the model to describe fluid flow, i.e. the Navier-Stokes equations (NSE), is pathological in nature, meaning that in some cases, it yields solutions that are counter-intuitive. For example, velocity of fluid flow or its vorticity can reach infinite values after a certain finite-time, for a given initial condition. This is counter-intuitive because we do not see water or a general liquid exploding (unless some adiabatic shock at larger Mach numbers happens) in reality. This pathological nature of fluids of reaching singular values is captured very well by an open millennium-prize problem formulated by the Clay Mathematical Institute in the dawn of 21st century. To state the problem briefly, let us first formally describe the Navier-Stokes equations.

Navier-Stokes equations, are Newton's laws of motion to model the motion of a fluid, in two or three spatial dimensions (\(\mathcal{R}^2 \textrm{or} \, \mathcal{R}^3\)), and single time \(t\) dimension. The velocity vector field \(\vec{u}(x,t) = (u_{i}(x,t))_{1 \leq i \leq n} \in \mathcal{R}^n\) and scalar pressure field \(p(x,t) \in \mathcal{R}\) are the unknowns in the equations. Given an assumption of incompressibility of the fluid, these equations are given by

\( \partial_t \vec{u}(t,x) = \nu \Delta \vec{u} - \sum_{i=1}^3 u_i \partial_i \vec{u} - \vec{\nabla} p + \vec{f} \)

(1a)

\( \nabla.\vec{u}=\sum^3_{i=1} \partial_i u_i = 0 \)

(1b)

where \(\nu\) is the kinematic viscosity and \(\vec{f}\) is the external body force. The initial conditions of the velocity vector field are given as

\( \vec{u}(0,x)=\vec{u}_0 (x) \)

(2)

where (1) and (2) are defined for \(t \geq 0\) and \(x \in \mathcal{R}^n\). The solutions to either of these equations are considered "well-behaved" or physically reasonable if

\( p,u \in C^\infty (\mathcal{R}^n \times [0,\infty)) \)

(3a)

\( \int_{\mathcal{R}^n} |u(x,t)|^2 dx < C \)

(3b)

for all \(t \geq 0\). Here, \(C^\infty\) refers to the functions \(p,u\) being smooth and infinitely differentiable, and the kinematic energy of the fluid is bounded above by a constant \(C\).

The original problem statement proposed by the Clay Mathematical Institute is to prove either of the following statements:

1. For \(\nu>0\) and \(n=3\), prove that for the smooth, divergence-free, physically reasonable initial vector field \(u_0(x)\), and \(f(x,t)=0\), there exists smooth functions \(p(x,t),u_{i}(x,t)\) on \(\mathcal{R}^3 \times [0,\infty]\) that satisfy (1) - (3).
2. For \(\nu>0\) and \(n=3\), prove that for the smooth, divergence-free, physically reasonable initial vector field \(u_0(x)\), and \(f(x,t)=0\), there exists no solutions \(p(x,t),u_{i}(x,t)\) on \(\mathcal{R}^3 \times [0,\infty]\) that satisfy (1) - (3).

While there have been many efforts to prove one of these statements, there has been no resolution to this date of this problem yet. Efforts in the past century focused on finding weak analytic solutions to certain modified version of the Navier-Stokes equations, which could have led to the proof of the first statement that the solutions are smooth in nature. These efforts include the works of: Leray; Constantin & Fefferman; Ladyzhenskaya-Prodi-Serrin and many others. However, only recently, in the past two decades, the focus of the community has now shifted to proving that the solutions might yield singularity at finite-time, and are, thus, non-unique. This is exemplified by the recent works of Buckmaster and Vicol [1], and broadly in the recent papers by Terence Tao. The next section will further expand on Tao's work and how it has paved a new path for potentially resolving the Navier-Stokes regularity/singularity debate.

3. Recent progress in the computational complexity of fluids

This section, specifically, highlights a new scheme to approach the regularity problem using ideas from theoretical computer science. In 2015, Terence Tao introduced a model [2]

\( \partial_t X_n = - \lambda^{2n\alpha} X_n + 1_{n-1=n(t)}\lambda^{n-1}X^{2}_{n-1} \\ - 1_{n=n(t)}\lambda^{n=n(t)}\lambda^{n}X_{n}X_{n+1} \)

(4)

where \(n: [0,T_{*})\to\mathcal{Z}\) is a piecewise constant function that describes the mode pair (\(X_{n(t)},X_{n(t)+1}\)) which is allowed to interact at a given time \(t\); \(X_{n}\) is the energy of fluid at scale \(n-1\) that is being diffused to the scale \(n\). It should be noted that here, the solutions to NSE are sought in terms of wavelengths/modes, instead of length scales. This interpretation usually comes from the Fourier transform of Navier-Stokes equations from the physical space to wavenumber space. Within this wavenumber space, a system of ODEs were constructed to simulate the Eq. (4) using a sequence of "quadratic circuits" connected in series fashion. Each circuit is composed of "quadratic logic gates" which simulate a certain form of basic quadratic non-linear interaction. The gates transfer energy from one mode to another using "amplifier" and "rotor" gates. Tao argued that it might be possible that such gates are Turing complete i.e. embeddable in a Turing machine. This construction was originally intended to exemplify an artificial case where the solutions to the artificial fluid flow exhibited blowup, wherein the dynamics of fluid was described in discretely self-similar fashion using Eq. (4). After 5 years, in 2021, Cardona, Miranda, Peralta-Salas, Presas [3] proved that the case hypothesised by Tao is indeed true for inviscid Navier-Stokes equations, in that these equations are Turing complete. The theorem that the authors proved states that

Theorem 1. There exists a Riemannian manifold \((M,g)\) whose Euler flow is Turing-complete: the halting problem for any given Turing machine is equivalent to the Euler flow for a certain initial condition associated to that machine entering a certain region.

where the authors constructed solutions for the steady Euler flow (without viscosity) on a Riemannian 3-sphere \(\mathcal{S}^{3}\) that are Turing complete. Following this work, the authors extended their analysis to a standard Euclidean 3-dimensional space. An intuitive sense of how the proof is derived can be given as follows. For a given string of symbols of the alphabet \((t^{*}_{-k},....,t^{*}_{k})\) and a Turing machine \(T\) with an input tape \(t\), the authors showed that it is possible to construct explicitly a point \(p\) and an open set \(U\) in \(\mathcal{S}^{3}\) such that when the velocity field \(X\), which is the solution of inviscid Navier-Stokes equations, passes through \(p\), it also intersects \(U\) if and only if \(T\) halts with the output tape at positions corresponding to symbols \((t^{*}_{-k},....,t^{*}_{k})\) (Fig. 1(a)). The authors found that if the initial vector field \(\vec{X}\) for Euler equations is given as an input in the NSE, the resulting velocity field can only simulate a finite number of steps, and thus, the Turing completeness of Navier-Stokes equations would still remain unproven.

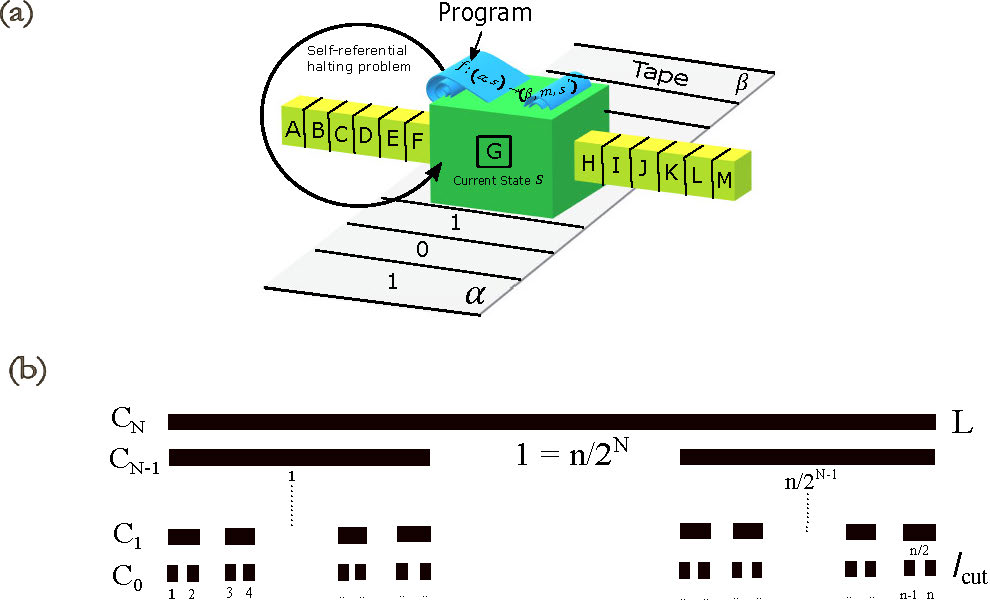
Figure 1. (a) Schematic of a Turing machine on a tape with input \(\alpha\), program/function \(f\), and output \(\beta\), (b) Cantor set framework consisting of \(N\) layers with length scale \(L\) of the top-most one and \(l_{cut}\) of the bottom-most one. There are \(n\) discrete elements in the bottom-most layer, and the number of elements reduce by a factor of 2 as one goes bottom-up layer by layer. Each layer is represented by \(C_i\), where \(0\leq i \leq N\).

As discussed by Tao, proving the Turing-completeness of the Euler or Navier-Stokes equations is the first step towards building, designing, and quantifying the design of logic gates that can be assembled to simulate the classical laws of conservation of energy and helicity that the fluid equations obeys. After making sure that the physics is right and the design of logic gates is rigorous enough, such a "fluid program" can be shown to blowup for a specific set of initial data, and the debate of regularity versus blowup can be given more concrete answer, for a given choice of initial data.

4. Cantor set framework for emergence of fluids from atoms

In recently uploaded two preprints, one of which is due to be published in the Int. J. Unconventional Computing [5] and the other one under review in JFM [6], we discussed the importance of "fluid computing" idea in the context of Navier-Stokes regularity problem. While the tools from reservoir computing and neuromorphic computing disciplines might be helpful to expound more on how fluids as computers might be dealt with, the focus that we draw in this section here is the theoretical treatment of fluid as a computer. To digitise fluids, it is important to think of a theoretical framework that can be used to program the behaviour of fluids emerging from atoms/molecules, and one such framework is Cantor set.

To understand emergence in fluids and how Cantor set is relevant there, we are interested to analyse two arbitrary length scales in a fluid: \(l_{cut}\) and \(L\), such that \(l_{cut}<<l\) \(l="1\)" \(l_{cut}="10^{-9}\)">single Cantor set denoted by \(\mathcal{C}_{N}\). From Fig. 1(b), it is apparent, geometrically, that the sets at layer \(k\) merge pairwise, to form the sets at layer \(k+1\). Thus, if the number of subsets in \(C_{1}\) are \(n\), the the number of subsets in \(C_{2}\) are \(n/2\), and so on, until \(C_{N}\). Since \(C_{N}\) is a single set with just one subset (itself), \(n/2^{N}=1\). Rearranging it </l\)>

\( N = \log_{2} n \)

(5)

At a general length scale, say \(l\) (\(l_{cut}\leq l \leq L\)), with the atoms categorised in the set \(C_{k}\), let us call each subset in \(C_{k}\) as a "mode". Consider any two adjacent modes in \(C_{k}\), say \(x\) and \(y\) with energies \(e_{x}\) and \(e_{y}\). At an initial time step \(t_{0}\), the modes are represented by \(x(t_{0})\) and \(y(t_{0})\). Consider them rotating around the origin at a constant angular rate \(\alpha z(t_{0})\) such that

\( x(t)=x(t_{0}) \cos(\alpha z(t_{0})) (t-t_{0}) - y(t_{0}) \sin (\alpha z(t_{0})(t-t_{0})) \)

(6)

\( y(t)=y(t_{0}) \cos(\alpha z(t_{0})) (t-t_{0}) + x(t_{0}) \sin (\alpha z(t_{0})(t-t_{0})) \)

(7)

\( z(t)=z(t_{0}) \)

(8)

where the mode \(z \in C_{k+1}\) is fixed while \(x,y \in C_{k}\) is not. In fact, starting at \(t_{0}\) until time \(T_{k}\), the two modes \(x\) and \(y\) interchange energy with each other and thus mix to emerge and form the mode \(z\) at the layer \(C_{k+1}\). This process can be viewed as \(z\) mode driving the exchange of energy between \(x\) and \(y\) modes. It is to be noted that though it is the choice of the reader to see the Cantor set in either top-down or bottom-up fashion, throughout this article, we choose to discuss emergence as a bottom-up process, starting from \(l_{cut}\) and reaching layer-by-layer until \(L\).

Equipartition theorem in statistical mechanics gives us

\( \alpha z (x^{2}-y^{2})=\partial_{t}(xy) \)

(9)

which can be written as

\( \alpha \int^{T_{k}}_{t_{0}} z(t)(x^{2}-y^{2})dt = x(T_{k})y(T_{k})-x(t_{0})y(t_{0}) \)

(10)

such that \(x^{2}+y^{2}=E\) and constant \(z\) gives

\( \frac{1}{T-T_{0}}\int^{T_{k}}_{t_{0}}x^{2} (t) dt = \frac{E}{2} + O(\frac{E}{\alpha |z(t_{0}|)(T-T_{0})|}) \)

(11)

where \(E=e_{x}+e_{y}\) and \(e_{x}=e_{y}\). As a result,

\( e_{x}=e_{y} = e[C_{k}] \approx \frac{e[C_{k+1}]}{2} \)

(12)

Using (12) and (5), one gets the general formula

\( e[C_{N}] \approx 2^{N} e[C_{1}] \)

(13)

which relates the energy of a discrete block in \(C_{1}\) (molecular scale) to the energy in \(C_{N}\) (continuum scale). To put forth an example where molecular scale physics is connected to continuum scale physics, consider a fluid \(F\) with surface tension \(\gamma\) which is composed of molecules in two layers separated at a distance \(d_0\), such that the surface energy can be defined as: \(\gamma = A / d_0^{6}\) where \(d_0\) is the intermolecular distance between two layers. Typical units of \(A\) could be \(10^{-20}\) J, while the units for \(\gamma\) is usually of the order of \(10^{1}\) J. Thus, a Cantor set framework if embedded into such a situation will yield the energy ratio of \(10^{-21}\) J, and thus, \(N \approx 70\) layers in the Cantor set framework. There are plenty other nano-to-micro scale physics connections in fluids that can be understood using the Cantor set framework, and in the future, we expect to produce a catalogue of such studies.

5. Fluids as chaotic systems and computers

Navier-Stokes equations are a type of chaotic dynamical system that can have solutions existing in an attractor of a particular dimension. However, the lack of a regularity proof prevents the existence of a global attractor for the equations. Nevertheless, it is still possible to circumvent this problem by introducing \(sup_{t} H_{1}\) and defining energy dissipation rate \(\overline{\epsilon}\) and Kolmogorov length scales \(\Lambda_{K}\) respectively as follows

\( \overline{\epsilon}= \nu L^{-3} \left(sup_{t} H_{1} \right) \quad , \quad \Lambda_{K}^{-1}=\left(\frac{\bar{\epsilon}}{\mu^{3}} \right) ^{1/4} \)

(14)

which is then used to estimate the attractor dimension. Such chaotic systems can be represented by a horseshoe map called shift map given by \(\sigma: a_{i} \rightarrow a_{i+1}\) where \((a_{i})=...a_{-2}a_{-1}.a_{0}a_{1}a_{2}...\) denotes a point in the Cantor set that represents all the past and future states of the trajectory of the dynamical system. Another version of this shift map is called a generalised shift map given by \(\phi: a \rightarrow \sigma^{F(a)} (a \oplus G(a))\) where \(F\) and \(G\) are maps from \(a\) to integers and \(a\) to finite sequences [4]. It is possible to embed a generalised shift map in a Turing machine using the following equivalence

\( (s,..,t_{-2}t_{-1}t_{0}t_{1}t_{2}...) \rightarrow ... t_{-2}t_{-1}.st_{0}t_{1}... \)

(15)

where \(s\) is the internal state and \(t_{i}\) is the internal tape. Thus, a Turing machine can represent the output of GS maps, and thus of a chaotic dynamical systems trajectory. This equivalence hints that there might exist some classes of Navier-Stokes equations which could be embeddable in a Turing machine. While much of these thoughts remained conjectural for two decades, only recently, in 2021, this debate was settled by proving that Euler equations are Turing-complete, whilst still keeping the Navier-Stokes Turing completeness problem as open.

6. What's next?

This article attempted to put forward arguments for why fluids suffer from a mathematical pathology that is inherent in the formulation of Navier-Stokes equations. One thing that is clear, and well-accepted in the community is that the continuum assumption in mechanics is a prime reason for the occurrence of singularity at scales close to the atomic length scale. It is then natural to attempt to understand the reason why the continuum assumption still works quite satisfactorily when applications of the hydrodynamic models are concerned, and how to rationalize this assumption mathematically. One possible way out is that there might be some fundamental equivalence between the continuum hypothesis in set theory and in fluid mechanics. In set theory, the continuum hypothesis disallows the existence of an infinity between the infinities of natural numbers and real numbers. This hypothesis allows the creation of null sets, such as Cantor sets, with measure zero, such that they are non-empty and not filled at the same time. Using such sets, it is possible that the pointwise property of a fluid defined at all points in the system is equivalent to the average property of the subset of a Cantor set which fills up the entire system in a similar cardinal fashion. This line of thought is still a work in progress and we do hope to prove in the coming months that the continuum hypothesis in set theory does allow continuum assumption in fluid mechanics to work.

We also discussed Cantor set framework to correlate arbitrary lower scales to higher scale. Though this idea might seem to be theoretical in nature yet, it can also be looked from an engineering and design lens. Recently, Song et al. (2022) [7] showed that the linear viscoelasticity of arrested soft materials (gels, glasses) at a macroscopic level is correlated to the microscopic dynamics of the material. At the macroscopic level, the stress relaxation of the system is studied using rheometry techniques. On the other hand, at the microscopic level, the superdiffusive dynamics of microscopic clusters are studied by perturbing the material using X-ray photo correlation spectroscopy. The nonlinear phenomenon at the smaller scale is physically correlated to the linear phenomenon at the macroscopic scale. An experimental understanding of this correlation can inform design experts to interfere and perturb the lower scale phenomenon in such a way that the desired output at the macroscopic level is reached. The techniques of physical learning (supervised or unsupervised) could be useful here to train and adapt a physical system to reach a desired target property by experimentally perturbing its internal nodes and adjusting the weights of the network in accordance with the physical law governing the emergent process.

In this article, we also discussed the recent advancements in the field of Navier-Stokes regularity problem, especially after the pioneering work of Tao. Given that this problem lies at the heart of current scientific advances of the 21st century, it is highly likely that the theoretical and numerical advances in physics-informed machine learning techniques and its connections to the computational complexity of ‘computable’ fluid parcels are going to metamorphosize our understanding of fluids in the coming few decades.

References

[1]   T. Buckmaster and V. Vicol, Nonuniqueness of weak solutions to the Navier-Stokes equation, Annals of Mathematics, 189(1), 2019, pp. 101-144.

[2]   T. Tao, Finite time blowup for an averaged three-dimensional Navier-Stokes equation, Journal of the American Mathematical Society, 29(3), 2016, pp. 601-674.

[3]   R. Cardona, E. Miranda, D. Peralta-Salas, and F. Presas, Constructing Turing complete Euler flows in dimension 3, Proceedings of the National Academy of Sciences, 118(19), 2021, e2026818118.

[4]   C. Moore, Unpredictability and undecidability in dynamical systems, Physical Review Letters, 64(20), 1990, p. 2354.

[5]   S. Sharma, G. Marcucci, and A. Mahmud, A complexity perspective on fluid mechanics, arXiv preprint arXiv:2212.00153, 2022.

[6]   S. Sharma and G. Marcucci, From Navier-Stokes millennium-prize problem to soft matter computing, arXiv preprint arXiv:2212.01492, 2022.

[7]   J. Song, Q. Zhang, F. de Quesada, M.H. Rizvi, J.B. Tracy, J. Ilavsky, S. Narayanan, E. Del Gado, R.L. Leheny, N. Holten-Andersen, and G.H. McKinley, Microscopic dynamics underlying the stress relaxation of arrested soft materials, Proceedings of the National Academy of Sciences, 119(30), 2022, p.e2201566119.