Handling editor: Evelyn Sander
Sensor Networks, Algebraic Topology, and Dynamics
Robert Ghrist, Departments of Mathematics and Electrical
& Systems Engineering, University of Pennsylvania
Imagine a future in which physical surroundings "wakes up," being
endowed with sensory data, networked and responsive. This is one of
the goals of the rapidly-developing field of pervasive sensor
networks. The ability to fabricate increasingly small sensing
devices, along with the computational scaling implicit in Moore's
Law and the parallel advances in wireless technology, foretell a
world in which walls, furniture, roads, vehicles, grocery bags, and
clothes are seemingly alive with data.
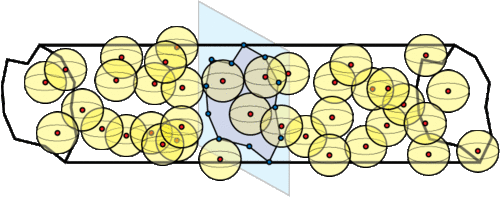
Figure 1. Ubiquitous sensing --- the prospect of ubiquitous
immersion of sensors --- leads to problems of
aggregating local data into global information.
Data: Good in Moderation
While it does not tax the imagination to contemplate a
trajectory for networked sensors which parallels that of
networked computers, managing vast networks of embedded sensors
does pose difficult engineering challenges. Some of the most
pressing challenges are as follows:
1. Too Much Data: What is to be done with all the local data
that is collected? How can it be suitably integrated so as to keep
data flows to a reasonable level? How can one effectively manage
uncertainty and faulty data?
2. Not Enough Power: The prime resource to be conserved in a
sensor network is power. Changing the battery on a sensor is a
bother, but changing the batteries on millions of sensors is a
barrier. Power constrains not only the type of sensing that may be
performed, but also -- more crucially -- the amount of communication
a network can bear. The ``viscosity'' of data in a network is
inversely related to the power consumed.
3. Who? What? Where? When?: Some types of data are unwieldy
to a frustrating degree. Clocks, for example, provide a challenge,
not because they are expensive, but because they are difficult to
synchronize across a network with (inevitable) signal delays.
Localization (knowing one's location) sounds easy in the context of
GPS, but a GPS device is neither cheap nor local. Some data is
simply too expensive to garner en masse.
Minimality: Less is more
In the context of constraints on resources, one option is to make do
with less or coarser data. This is where the engineering challenges
of pervasive sensing become a mathematical challenge: what is the
minimal amount of data needed to solve a given sensing problem? If
mathematicians can demonstrate a clever means of solving a problem
without needing the expensive signal processing of a target
identifier, or a GPS, or a distance-with-bearing measurement, then
this can lead to vast improvements in performance. As well, if a
particular sensor modality is shown to be redundant, this simplifies
the miniaturization and manufacturing of sensors, by lowering the
device capabilities. A similar reduction in complexity occurs if one
can increase the tolerance for noisy data: better mathematics makes
the engineering task simpler.
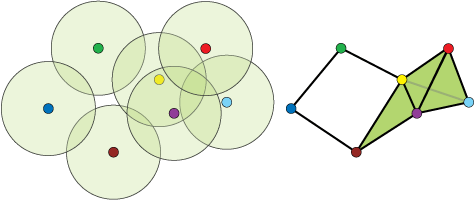
Figure 2. There is a natural way to turn coverage regions
of sensors into a simplicial complex.
Algebraic Topology and Sensors
What is the appropriate mathematics for sensor networks? Most of the
problems in networked sensing are of the local-to-global variety. As
sensors shrink in size and increase in multiplicity, one goes from
having a small number of ``global'' sensors to a dense array of
``local'' sensors. Sensing problems are increasingly about
integrating localized data into a global picture of the environment.
Among the many applicable tools that mathematicians have discovered,
one branch of mathematics is outstanding in its fine-tuned ability
to turn local data into global data: algebraic topology. This branch
of mathematics is rarely construed as applied; nevertheless, it is
almost perfectly designed to answer questions in sensor networks.
Algebraic topology takes as its argument an abstract space and a
rough equivalence relation (homotopy type, homology type, or other
type of ``deformation'') and reduces it to algebraic data (groups,
rings, modules, etc.). The space is generally encoded as local, or
even combinatorial, data, in a manner reminiscent of what is encoded
in a sensor network (nodes, local communication links, etc.). Very
sophisticated algebraic structures arise from a principled approach
to topological data. One such tool is homology (with real
coefficients): a means of reducing a topological space X to a
sequence of vector spaces Hk(X), whose dimensions
encode the number of various types of holes in a space, and whose
bases describe said holes.
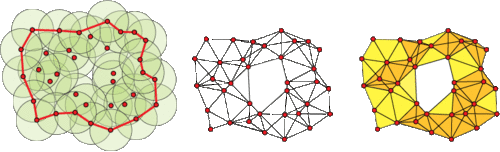
Figure 3. Homology detects the presence of a hole within
a network of sensors having no knowledge of
coordinates or distance.
Example: Coverage
A simple example will suffice to demonstrate the efficacy of
algebraic-topological methods. Consider a network of labeled sensor
nodes whose communication links are based on proximity: nodes which
are roughly nearby can communicate. Assume that each node is a
sensor, responsible for ``covering'' a neighborhood of its location.
One of the important problems in sensor networks is the coverage
problem -- are there holes in the domain which are not covered
by sensors?
If the nodes have no knowledge of their coordinate locations or of
the locations of their neighbors, how can they determine whether
there are gaps in coverage? Imagine a cocktail party full of people,
blindfolded, and constrained to do nothing but whisper their
identities and listen for the names of their immediate neighbors
(with one ear, to prevent bearing data). Can such a crowd
determine the topology or geometry of the party?
Some assumptions on the sensor modality and the communication
protocols must be made. Weak assumptions would be as follows. Assume
nodes lie in the plane, at unknown locations. Assume that any
collection of K nodes that are in pairwise communication have
coverage regions which contain the convex hull of these points in
the plane. So, if three nodes communicate pairwise, then the
abstract triangle they form in the plane lies within the coverage of
the network. These are reasonable assumptions for a stable network
where communication links are based on proximity. This assumption
prompts the examination of a particular simplicial complex --
a space built from simplices -- whose vertices are sensor nodes;
whose edges are communication links; and whose K-simplices
correspond to collections of K+1 nodes in pairwise
communication. Denote this complex R.
Theorem: [DG] Assuming a sensing modality that covers convex
hulls of pairwise-communicant nodes in the plane, the region spanned
by a cycle F in the communication graph is covered if F
is nullhomologous in H1(R,F).
This provides a simple homological coverage criterion. (It is
not if and only if, since our assumptions on coverage allow nodes to
cover more than the convex hulls of simplices.) The proof of this
result is a simple exercise in using exact sequences and commutative
diagrams in homology. One can do much more: coverage in
time-dependent systems, criteria for hole repair, and minimizing the
number of nodes needed to form a cover, all fall out of the
homological algebra in a natural way.
The question remains: how easy is it to compute these homological
invariants, and to what extent can the computation be performed in a
local, distributed manner? Fortunately, there has been an explosion
of work in the past decade in computational homology, much of the
impetus coming from dynamical systems and Conley index theory for
differential equations [KMM].
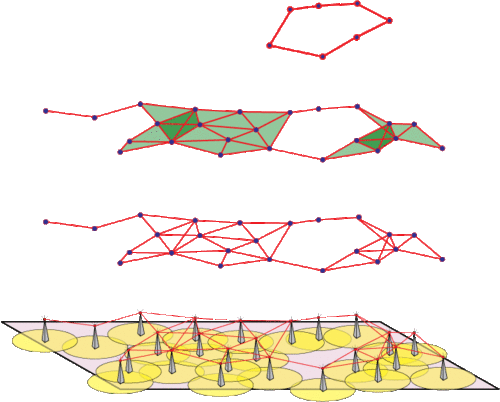
Figure 4. A physical network of sensors is approximated
by its communication network. This network, in turn,
is a frame or skeleton for a higher-dimensional
complex. The topology of this complex is linked
with the coverage patterns in the network.
A Dynamical Systems Perspective
Recent work of Jadbabaie and Muhammad [JM] gives a means of
computing the homology associated to a sensor network in a
distributed manner, using a dynamical system. It is well-known that
a combinatorial version of Hodge theory (which computes the homology
of a smooth manifold in terms of its harmonic forms) can be used to
compute the homology of a simplicial complex. The key insight in
[JM] is to use a dynamical system --- a Laplacian flow --- to
compute the combinatorial harmonic forms on a simplicial complex
associated to a sensor network (in much the same way that the heat
equation can compute a harmonic function in the smooth category). As
a dynamical system is used, the computation is purely local and
distributed: an especially exciting and useful feature.
Looking Forward
Coverage is but one example of algebraic topology impacting sensor
networks. Another example at the forefront of the field includes
using an integration theory derived from constructible sheaves and
Euler characteristic to perform target enumeration [BG]. This
provides a topological approach to data aggregation over networks.
Various forms of topological complexity answer questions about clock
synchronization in networks by means of cohomological obstructions
[CCCM]. Winding numbers provide means of surrounding targets in
networks without position information [GLPS]. These are merely the
first few applications of the richness of algebraic topology in
sensor networks. Most of these applications are for networks which
are entirely static: many of the most interesting open questions
concern the intricacies implicit in dynamic networks, where it is
clear that applied dynamical systems theory has much to say.
REFERENCES
| [BG] |
|
Y. Baryshnikov and R. Ghrist, ``Target enumeration
via Euler characteristic integrals,'' to appear, SIAM
J. Appl. Math., 2008.
|
| [CCCM] |
R. Calderbank, D. Cochran, F. Cohen, and B. Moran, ``Clock
synchronization on multi-hop networks,'' preprint, 2008.
|
| [DG] |
V. de Silva and R. Ghrist, ``Coordinate-free coverage in sensor
networks with controlled boundaries via homology,'' Intl. J.
Robotics Research, 25(12), 1205--1222, 2006.
|
| [GLPS] |
R. Ghrist, D. Lipsky, S. Poduri, and G. Sukhatme,
``Surrounding nodes in coordinate-free networks,'' in Proc.
Workshop in Algorithmic Foundations of Robotics, 2006.
|
| [2] |
[JM] A. Jadbabaie and A. Muhammad, ``Distributed computation of
homology groups by gossip,'' in Proc. American Control
Conference, 2007.
|
| [KMM] |
T. Kaczynski, K. Mischaikow, and M. Mrozek, Computational
Homology, Applied Mathematical Sciences 157, Springer-Verlag,
2004.
|