1. Asymptotic Expansions

Constructing asymptotic expansions for some given function is a versatile technique that can be found in the toolbox of many mathematicians. Truncating a formal asymptotic series expansion after a finite number of terms typically provides an accurate representation of the function it represents. Often, highly accurate mathematical approximations may be found by retaining only a handful of terms – one or two terms are sufficient to study system behaviour in many applications. If this is not sufficient, more terms can seemingly be taken until the required accuracy is reached.

Unfortunately, asymptotic series expansions seem to have a fundamental limit built into their construction. Consider using a Taylor series about \(\epsilon = 0\) to represent \(\mbox{e}^{-1/\epsilon}\), such that

\(\mbox{e}^{-1/\epsilon} = \lim_{k \rightarrow 0}\left[\mbox{e}^{-1/k} + \frac{\mbox{e}^{-1/k}}{k^2} \cdot \epsilon - \frac{(2 k - 1) \mbox{e}^{-1/k}}{2 k^4} \cdot \epsilon^2 + \ldots\right]. \)

(1)

In the limit that \(k \rightarrow 0\), each of these coefficients is zero. Furthermore, this pattern continues indefinitely, with every coefficient in this series begin given as zero. The power series is incapable of representing behaviour that is exponentially small in the asymptotic parameter \(\epsilon\), as it is smaller than any algebraic power of \(\epsilon\) in the limit that \(\epsilon \rightarrow 0\). Behaviour on an exponentially small scale cannot be represented in terms of a power series, as it lies "beyond all orders" of the series.

This does not seem to be a particularly troubling limitation. If some component of an asymptotic solution is exponentially small, then it seems as if it is unlikely to have any important implications for the solution of the system. However, there are certain situations in which the exponentially small terms play a pivotal role in the behaviour of a given system. Typically, these fall into one of three (often overlapping) categories:

1. Uniformly valid asymptotic expansions. Systems that contain behaviour that is exponentially small in one region of the function domain, but grow to become significant elsewhere [2, 3, 6].
2. Important qualitative behaviour present at exponentially small scales. This is seen, for example, in the study of water waves in certain physical limits [13, 14]; the water waves are exponentially small, and do not appear at any algebraic orders in the solution expansion. An example of this is shown in Figure 3.
3. Exponential selection problems. Many systems are well-posed at all algebraic orders, but have boundary conditions that cannot be satisfied at exponentially small scales [11, 19, 22]. In these systems, behaviour that occurs on exponentially small scales dramatically impacts the overall system behaviour at every order. An example of this is shown in Figure 4, in which steady translating bubble solutions can only exist for certain parameter combinations.

The importance of exponentially small terms in a range of systems could not be ignored, and eventually a range of techniques were developed, based on the pioneering works on late-order asymptotics by Dingle [15] and resurgence by Écalle [16], to obtain asymptotic approximations which include exponentially small terms. These techniques are found in the literature under many different names, including exponential asymptotics, hyperasymptotics, or asymptotics beyond-all-orders [9, 10]. While the details of each method vary, they typically involve some variant of the following steps.

The first step is to write the solution as some asymptotic power series in the appropriate limit. While this series is not able to capture exponentially small behaviour, it still plays an important role in exponential asymptotic methods. A representative series for some function \(g(z;\epsilon)\) in the limit that \(\epsilon \rightarrow 0\) may take the form

\(g(z;\epsilon) \sim \sum_{n=0}^{\infty} \epsilon^n g_n(z) \quad \mathrm{as} \quad \epsilon \rightarrow 0. \)

(2)

If exponentially small terms play a significant role in the problem, then this series typically diverges for any nonzero \(\epsilon\) [10]. The key observation that makes exponential asymptotic methods was made in [4, 5], in which it was shown that if a divergent asymptotic series is truncated such that the error is minimized, then the error of the truncated series is exponentially small. This is known as optimal truncation. The next step in exponential asymptotic methods typically involves obtaining the optimally truncated series. This can be accomplished using Borel summation, late-order term asymptotics, or a number of other related techniques. After optimal truncation, we write

\(g(z;\epsilon) = \sum_{n=0}^{N_{\mathrm{opt}}} \epsilon^n g_n(z) + R_N(z;\epsilon), \)

(3)

where \(N_{\mathrm{opt}}\) is the number of terms that minimizes the approximation error. Note that this expression is an equality, and the quantity \(R_N\) therefore represents the approximation error obtained by optimal truncation.

The final step is to rescale the problem to examine \(R_N\) directly. As \(R_N\) represents the exponentially small contribution to the solution behaviour, this is equivalent to isolating the exponentially small terms, allowing them to be studied and manipulated directly. The precise method for capturing \(R_N\) depends on the exponential asymptotic method being used, and the form of the equation, but these methods have the common property that the exponentially small terms are separated from the algebraic behaviour through some rescaling.

2. Stokes' Phenomenon

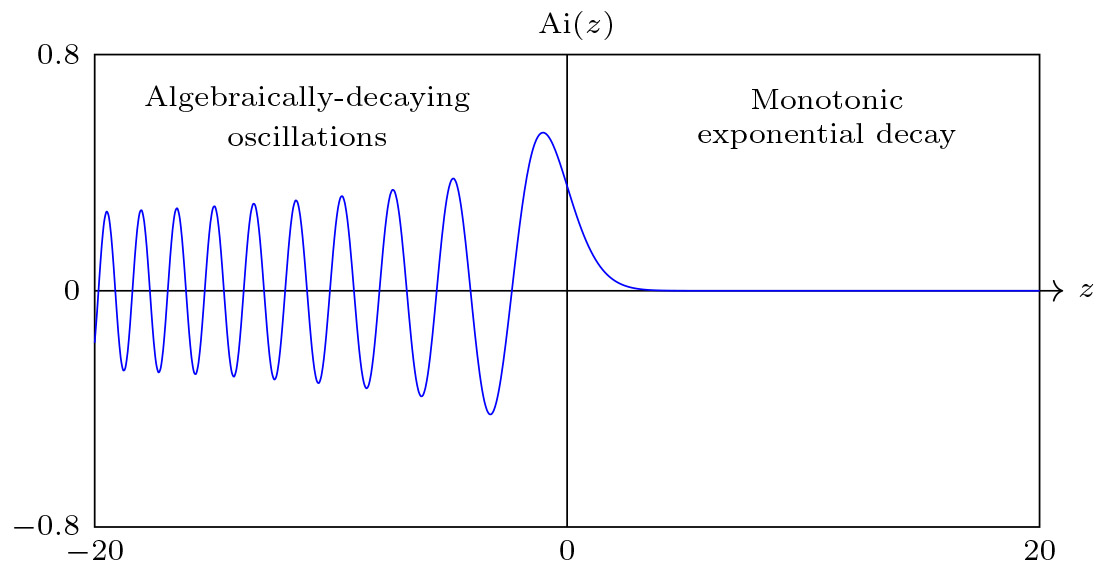
Figure 1. The Airy function of the first kind. In the limit that \(z \rightarrow \infty\), the function decays exponentially without oscillation. In the limit that \(z \rightarrow -\infty\), the function oscillates and decays algebraically with amplitude that is \(\mathcal{O}(|z|^{-1/4})\) in the limit.

With the advent of exponential asymptotic methods, it became possible to explore exponentially small effects in systems. On this scale, solutions can exhibit unusual behaviour, such as "Stokes' Phenomenon". Stokes' Phenomenon was named after its discoverer, G. G. Stokes, who was studying solutions to the Airy equation [24], given by

\(\dfrac{\textrm{d}^2y}{\textrm{d}z^2} = zy. \)

(4)

This differential equation has two solutions. One of these, known as the Airy function of the first kind and denoted \(\mathrm{Ai}(z)\), describes the diffraction of light; it decays exponentially in the positive direction, and oscillates in the negative direction. The behaviour of this function is illustrated in Figure 1. Stokes was interested in understanding the behaviour of this function in the complex plane, and how these two different asymptotic behaviours could be connected.

The asymptotic behaviour of the Airy function \(\mathrm{Ai}(z)\) for large \(|z|\) is composed of a linear combination of two exponential contributions, such that

\(\mathrm{Ai}(z) \sim \frac{A_1}{z^{1/4}}\mbox{e}^{-2z^{3/2}/3} + \frac{A_2}{z^{1/4}}\mbox{e}^{2z^{3/2}/3}. \)

(5)

For simplicity, we define

\(f_1(z) = \frac{1}{z^{1/4}}\mbox{e}^{-2z^{3/2}/3},\qquad f_2(z) = \frac{1}{z^{1/4}}\mbox{e}^{2z^{3/2}/3}, \)

(6)

such that the asymptotic behaviour of \(\mathrm{Ai}(z)\) is a linear combination of \(f_1\) and \(f_2\).

On the real axis it must be true that the limit as \(z \rightarrow \infty\) is described by \(A_2 = 0\). If \(A_2\) was not zero, the exponential term \(f_2\) would dominate the asymptotic behaviour in this limit, which it does not. In the negative real direction, the oscillatory behaviour in the limit that \(z \rightarrow -\infty\) is created by the combined effect of contributions from both \(f_1\) and \(f_2\). Hence, both \(A_1\) and \(A_2\) must be nonzero in this limit. Stokes reasoned that the exponential contribution \(f_2\) must appear somewhere, and investigated the solution behaviour along an arc with large radius connecting the two limits.

Through laborious hand calculation, Stokes discovered that the asymptotic behaviour of this function changes dramatically in different sectors of the complex plane. These sectors are bounded by special curves, later named Stokes curves and anti-Stokes curves. These curves are illustrated in Figure 2. As a Stokes curve is crossed, exponentially small contributions rapidly appear or disappear, demonstrating behaviour is known as "Stokes switching". As an anti-Stokes curve is crossed, there is a change in the dominant exponential contribution; exponentially large terms become exponentially small, and vice versa (in a number of references on the topic of Stokes' phenomenon, the definition of Stokes and anti-Stokes curves is reversed).

Figure 2. Stokes curves and anti-Stokes curves in \(\mathrm{Ai}(z)\). It is clear from the decaying exponential behaviour on the positive real axis that \(A_1\neq 0\) and \(A_2 = 0\) in Region ①. There is an anti-Stokes curve along \(\mathrm{arg}(z) = \pi/3\), across which the exponentially small contribution associated with \(A_1\) becomes exponentially large in Region ②. There is a Stokes curve along \(\mathrm{arg}(z) = 2\pi/3\), across which \(A_2\) becomes nonzero, producing a new exponential contribution which is present in Region ③. Finally, there is an anti-Stokes curve along the negative imaginary axis, along which both exponentials are \(\mathcal{O}(1)\), producing oscillatory behaviour.

The Airy function \(\mathrm{Ai}\) in the upper half plane contains one Stokes curve and two anti-Stokes curves. In the region containing the positive real axis it is impossible for \(A_2\) to be nonzero, as previously discussed. If it were present, then \(f_2\) would be exponentially large, and dominate the exponentially decaying behaviour caused by \(f_1\).

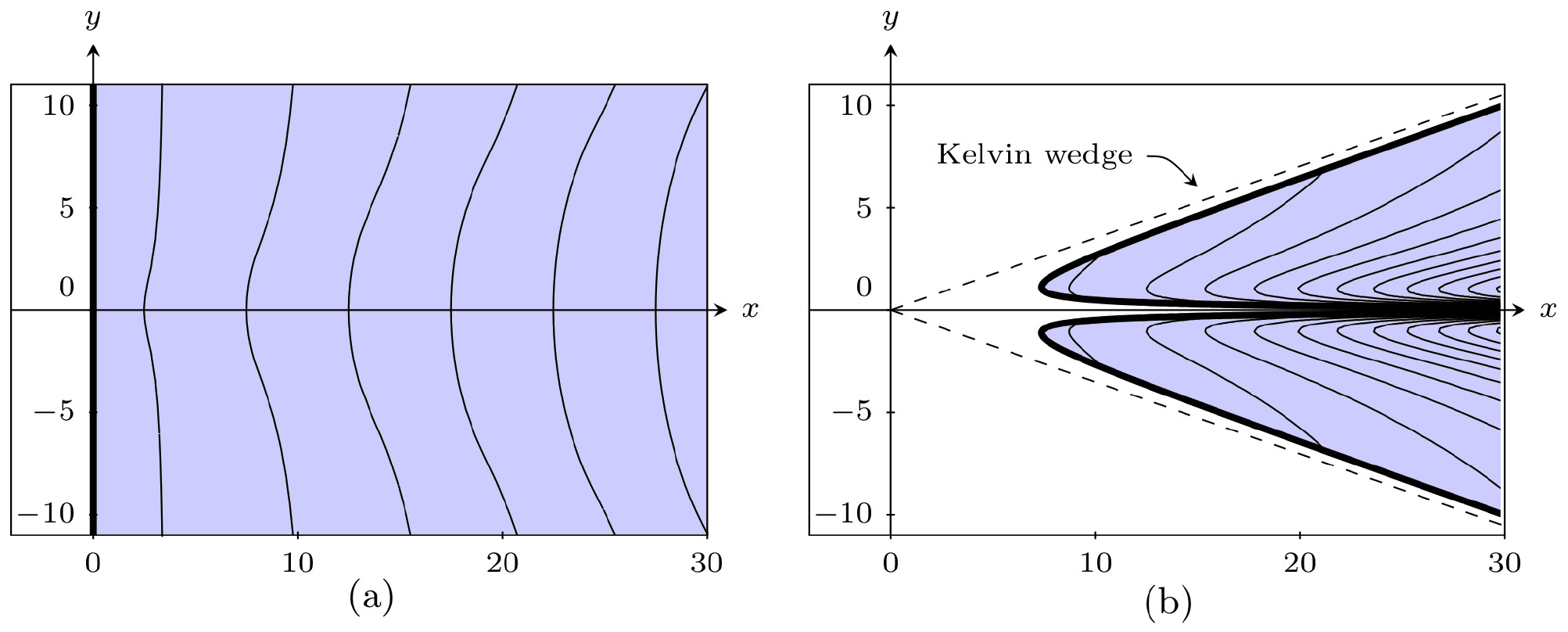
Figure 3. Stokes curves and equal phase lines for surface gravity waves in three dimensional flow past a submerged source propagating in a (a) parallel and (b) perpendicular direction relative to the background flow, created using calculations from [21]. The submerged source is located below \((x,y) = (0,0)\). Stokes curves are shown in bold, while equal phase lines are shown as narrow curves. The waves are switched on across the Stokes curves, and are present in the shaded area. Perpendicular waves are located entirely within a region known as the Kelvin wedge, which has an interior angle of approximately \(38.9^{\circ}\), while parallel waves propagate outwards, with the amplitude decaying exponentially outside of the wedge.

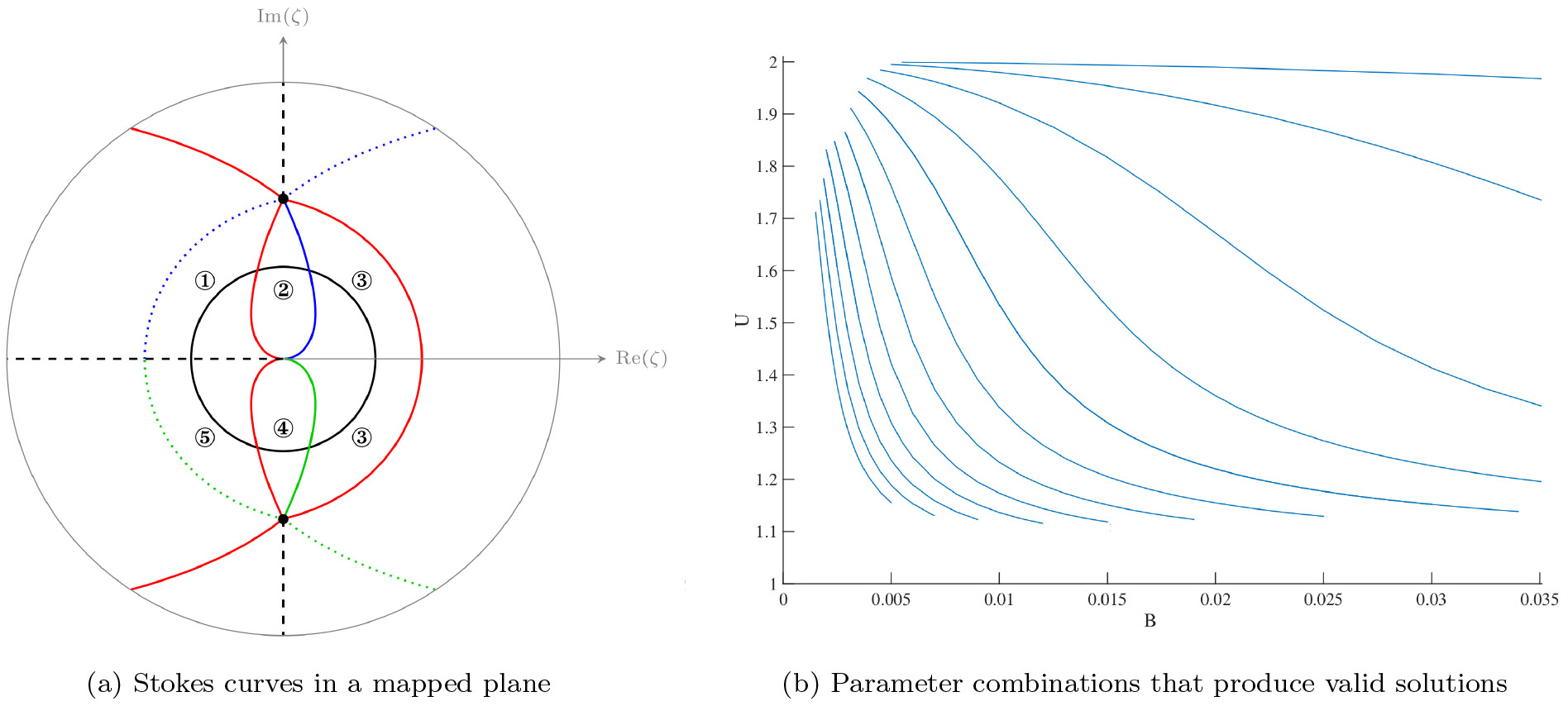
Figure 4. This figure illustrates a typical example of an exponentially small selection problem: a steadily translating bubble, created using calculations from [22]. In (a) the bubble has been mapped to the unit circle, depicted as a bold black circle. Anti-Stokes curves are shown in red, and important Stokes curves are shown as blue or green unbroken curves. Dotted curves and dashed black lines represent Stokes curves and branch cuts that do not impact the selection problem. On unit circle sections ① and ②, the exponential terms are absent. Two exponentially small terms switch on as the Stokes curves are crossed into sections ③ and ④. In section ⑤ an anti-Stokes curve has been crossed, and both contributions must be exponentially large. This is not possible, and therefore solutions can only exist if the two exponential contributions cancel precisely. This cancellation only occurs for specific combinations of the flow velocity \(U\) and surface tension parameter \(B\), shown in (b) as blue curves.

The curve \(\mathrm{arg}(z) = \pi/3\) is an anti-Stokes curve. As this curve is crossed, \(f_1\) changes from being exponentially small in the limit that \(|z| \rightarrow \infty\) to being exponentially large. There is no change in the coefficients \(A_1\) or \(A_2\) as anti-Stokes curves are crossed. However, the curve \(\mathrm{arg}(z) = 2\pi/3\) is a Stokes curve. As this curve is crossed, \(A_2\) changes rapidly and smoothly to a nonzero value, "switching on" the exponential contribution \(f_2\). Finally, on the negative real axis, both \(f_1\) and \(f_2\) are present, and their combined effect produces the oscillations seen in the limit that \(z \rightarrow -\infty\). By carefully tracking where the exponentially small quantity \(f_2\) switches on, it is possible to construct a uniform asymptotic expansion for \(\mathrm{Ai}(z)\), explaining the difference in asymptotic behaviour in the negative and positive real directions.

Locating Stokes curves, and studying the behaviour that switches as they are crossed, is a challenging task. The switching is always exponentially small compared to the dominant solution behaviour, and therefore inaccessible to classical asymptotic power series methods. Studying Stokes' phenomenon therefore typically requires the use of exponential asymptotic methods, which are designed for precisely this purpose.

Some examples of Stokes and anti-Stokes curves that play important roles are shown in Figures 3 and 4. Figure 3 shows waves on a the surface of a three-dimensional flow, which appear across Stokes curves. Figure 4 shows Stokes curves that select valid solutions for a steadily translating Hele-Shaw bubble, and the physical configurations that produce valid solutions. In both of these problems, exponential asymptotics were used to understand important aspects of the solution behaviour.

3. Nanoptera in Dynamical Systems

A particularly significant example of Stokes' phenomenon playing an important role in a physical system is the study of "nanopteron" solutions, or generalized solitary waves. Boyd introduced the concept of a nanopteron in his study of the \(\phi^4\) breather [7]. A nanopteron approximately satisfies the classical definition of a solitary wave – an exponentially localized wave that propagates without changing form – except rather than being completely localized, a nanopteron instead also possesses a small-amplitude oscillation on one or both sides of the central solitary wave. This oscillation is typically exponentially small, meaning that the wave is exponentially localized to all algebraic orders in the singular perturbation parameter. Examples of nanoptera are shown in Figure 5.

Figure 5. Comparison of the profiles associated with (a) a standard solitary wave, (b) a one-sided nanopteron, and (c) a two-sided nanopteron. The solitary wave is localized spatially, whereas the nanoptera contain exponentially small non-decaying oscillatory tails on (b) one side or (c) both sides of the wave front.

Nanoptera are typically found in the solutions to singularly-perturbed systems in which the unperturbed system contains solitary wave solutions. One of the earliest examples of this to be studied is the singularly-perturbed fifth-order Korteweg de-Vries (KdV) equation [8, 17, 27]. In this case, the system is singularly perturbed around the classical KdV equation, which possesses solitary wave solutions. Using one of these solitary wave solutions as the leading-order behaviour in an asymptotic expansion for the solution of the fifth-order KdV equation provided a way to construct nanopteron solutions to the singularly perturbed problem.

Solitary waves propagate indefinitely without changing form, but this is not necessarily true of nanoptera. When these solutions were first identified, it was commonly assumed that waves of this form were steady, and that these waves could propagate indefinitely in the same manner as classical solitary waves. This idea was contradicted by the work of Boyd [8], who concluded that only symmetric two-sided nanoptera could truly propagate in this manner. One-sided nanoptera, or two-sided nanoptera with unequal amplitude on either side, necessarily radiate energy and can therefore not propagate indefinitely. Hence, these solutions are not true travelling wave solutions, and are instead described as "metastable" or "quasi-stable" solutions.

This observation means that understanding the exponentially small oscillations in the solution is critically important in describing the long-time behaviour of the wave: will it propagate forever, or will it eventually collapse?

Using exponential asymptotic analysis, it is possible to show that many nanoptera contain a single Stokes curve in their solution, joining singularities in the analytically-continued upper and lower half planes. As this Stokes curve is crossed, waves are either switched on or off (in the case of one-sided nanoptera) or experience a jump in amplitude from negative to positive (in the case of two-sided nanoptera). An example of this behaviour is shown in Figure 6.

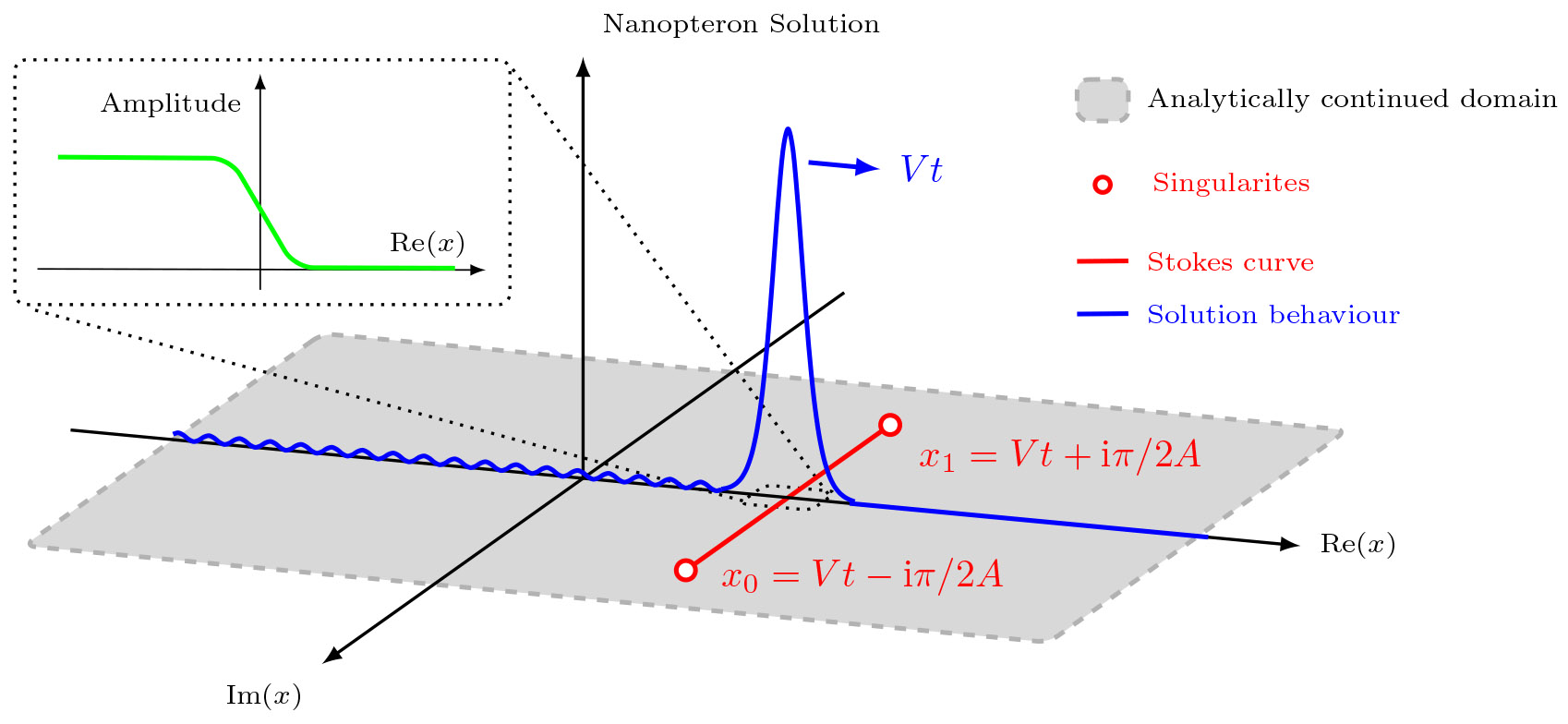
Figure 6. This figure illustrates the effect of Stokes' phenomenon on the exponentially small terms in a nanopteron with one Stokes line, originating at singularities in the analytically-continued complex plane. The solution is shown by a blue curve. The singularities and Stokes curves are represented by red circles and a red curve respectively. There are no disturbances ahead of the main wave, and an exponentially small train of oscillations appears as the Stokes curve is crossed. The amplitude of the oscillations near the Stokes line is shown in the inset figure as a green curve. These oscillations are visible in the wake of the main wave. As this is a one-sided nanopteron, it is clear that the wave must eventually lose energy and collapse, rather than propagating indefinitely. (Figure provided by Aaron Moston-Duggan.)

If the main wave is moving into an undisturbed domain, then the exponentially small oscillations must form in its wake. This has been shown in a number of partial differential equation systems, including [12, 18]. The oscillations appear only on the side of the Stokes curve that trails behind the central wave core. These oscillations require energy to form, and therefore the central wave must eventually collapse.

However, this isn't the end of the story. Recently, it was shown in [1, 23, 20] that many nanoptera in discrete singularly-perturbed systems actually contain two Stokes curves, rather than one. This means that the exponentially small contribution to the solution is composed of two exponentially small oscillations, rather than one. In Figure 7(a), the exponentially small contribution to the solution is shown for a system with two Stokes curves. The solution is undisturbed ahead of the central wave, with one set of oscillations switching on as each Stokes curve is crossed.

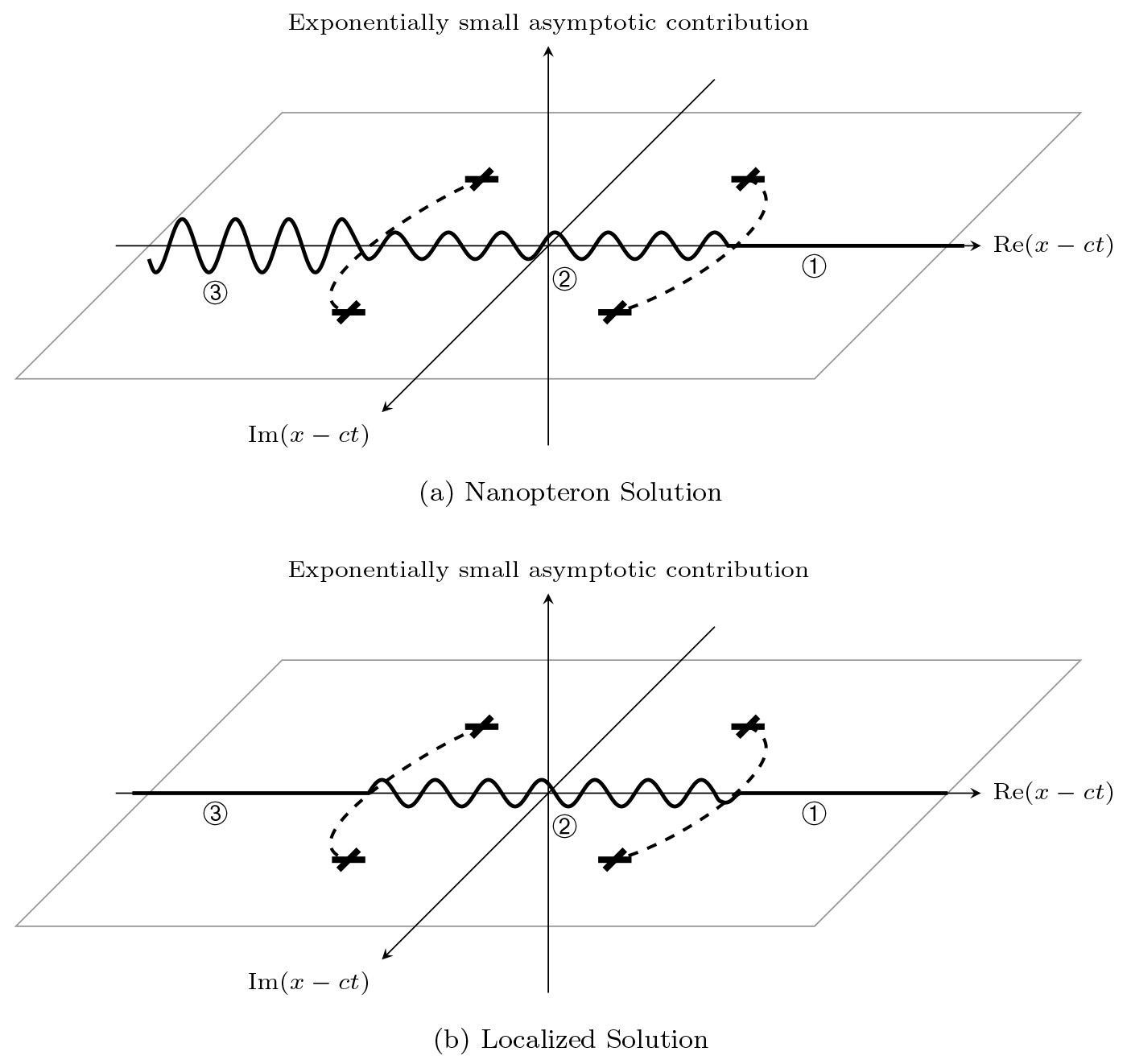
Figure 7. This figure illustrates the impact of Stokes' phenomenon on the exponentially small terms in a nanopteron with two Stokes lines, originating at singularities in the analytically-continued complex plane, denoted by crosses. In (a), the solution is seperated into three regions. Region ① is ahead of the main wave core, and contains no exponentially small contributions. In Region ②, one set of oscillations is switched on as the first Stokes curve is crossed. In Region ③, a second Stokes line has been crossed, and two exponentially small oscillatory contributions are present in the solution behind the main wave core. In (b), the behaviour is identical, except that the two solutions cancel each other out precisely, meaning that Region ③ contains no oscillations at all, despite both contributions having been switched on. In this case, the solution is a truly localized solitary wave.

Initially it seems like this makes the problem worse rather than better. Instead of one wave train drawing energy from the main wave core, there are two. However, this also allows for the possibility of wave cancellation. If the two wave trains cancel precisely, then the travelling wave is exponentially localized, and can propagate indefinitely without losing energy. This configuration is shown in Figure 7(b). In this case, both contributions are "present" in the wake of the central wave, but cancel each other out, causing the waves to be localized to a finite region between the Stokes curves. For most systems of this form, there is some infinite discrete set of solution parameters that localized solitary waves in this fashion. An example of this behaviour was identified for a diatomic Toda lattice in [26], and the asymptotic behaviour was obtained using exponential asymptotic methods in [20].

Using exponential asymptotics, it is possible to predict configurations in which the oscillations are localized, and the wave can propagate indefinitely. Nanoptera solutions for travelling waves in singularly-perturbed systems are therefore a striking example of systems that satisfy criteria 2 and 3 from Section 1. The oscillations are a qualitative behaviour that is only present on exponentially small scales, and therefore cannot be captured using algebraic series methods. Furthermore, the overall behaviour of the system is impacted significantly by these terms: they determine whether the wave propagates indefinitely, or eventually collapses.

There are many interesting open questions remaining in this field: one of these is to determine how the metastability of a one-sided nanopteron can be studied directly using the asymptotic solution. In [23, 20], as well as many other analyses such as the fifth-order KdV [17, 25], there is nothing explicit in the asymptotic solution which indicates that the wave must eventually collapse. While this can be seen from arguments using energy, it seems like metastability should be possible to observe in asymptotic solution directly for sufficiently large time. Obtaining this information likely requires a careful analysis of the interaction between algebraic and exponentially small scales in the problem on long time scales.

4. INI Research Programme

The use of exponential asymptotics to study Stokes' phenomenon has been used to provide insight into a range of physical problems. In addition to nanoptera in dynamical systems, Stokes phenomenon has been shown to play an important role in water wave problems (see Figure 3) and fluid interface behaviour (see Figure 4), crystal growth, and the theory of random matrices and orthogonal polynomials. Recently, remarkable progress has also been made in theoretical physics using the theory resurgent asymptotic analysis. This approach has revealed new insights into quantum field theories, string theory, and knot theory.

Advances in these areas have developed largely in parallel within the mathematics and theoretical physics communities. In order to unify the ideas that have grown in these areas, the Isaac Newton Institute for Mathematical Sciences is hosting a six-month programme entitled "Applicable resurgent asymptotics: towards a universal theory" from January to June, 2021. This programme has a very broad scope, and is intended to draw together many of the disparate exponential asymptotic approaches that have been developed to study problems arising in particular fields.

This programme intends to host several workshops which may be of interest to researchers who would like to develop more familiarity with exponential asymptotic techniques, including a Summer/Winter school aimed to introduce the topics at a level appropriate to postgraduate research students. This includes exploring the role of foundational works by Dingle and Écalle, how to identify physical problems in which exponentially small effects are important, and how to apply exponential asymptotic methods to uncover these effects.

It is hoped that efforts such as this programme will "demystify" exponential asymptotics, and that in the future, these methods will join classical asymptotic series methods as a standard component of the applied mathematics toolbox. It is not a coincidence that researchers discovered many new important exponentially small effects in the decades following the development of the first exponential asymptotic techniques; these tools permitted researchers to see behaviour which had previously been hidden, and showed that this behaviour plays a pivotal role in many physical and mathematical systems. It is expected that as the importance of these effects in many systems becomes more well-known, and exponential asymptotic methods become more accessible and widely used, the number of applications for these ideas will continue to grow.

References

[1]   G. L. Alfimov, A. S. Korobeinikov, C. J. Lustri, and D. E. Pelinovsky, Standing lattice solitons in the discrete nls equation with saturation, Nonlinearity, 32(9) (2019), p. 3445.

[2]   M. V. Berry, Stokes phenomenon; smoothing a Victorian discontinuity, Pub. Math. de L'IHÉS, 68 (1988), pp. 211–221.

[3]   M. V. Berry, Uniform asymptotic smoothing of Stokes's discontinuties, Proc. Roy. Soc. Lond. A, 422(1862) (1989), pp. 7–21.

[4]   M. V. Berry, Asymptotics, superasymptotics, hyperasymptotics, In H. Segur, S. Tanveer, and H. Levine, editors, Asymptotics Beyond All Orders, Plenum, Amsterdam, 1991, pp. 1–14.

[5]   M. V. Berry and C. J. Howls, Hyperasymptotics, Proc. Roy. Soc. Lond. A, 430(1880) (1990), pp. 653–668.

[6]   M. V. Berry and C. J. Howls, Hyperasymptotics for integrals with saddles, Proc. Roy. Soc. Lond. A, 434(1892) (1991), pp. 657–675.

[7]   J. P. Boyd, A numerical calculation of a weakly non-local solitary wave: the \(\phi^4\) breather, Nonlinearity, 3(1) (1990), pp. 177–195.

[8]   J. P. Boyd, Weakly non-local solitons for capillary-gravity waves: fifth-degree Korteweg-de Vries equation, Physica D, 48(1) (1991), pp. 129–146.

[9]   J. P. Boyd, The devil's invention: Asymptotic, superasymptotic and hyperasymptotic series, Acta Appl. Math., 56(1) (1999), pp. 1–98.

[10]   J. P. Boyd, Hyperasymptotics and the linear boundary layer problem: Why asymptotic series diverge, SIAM Rev., 47(3) (2005), pp. 553–575.

[11]   S. J. Chapman, On the rôle of Stokes lines in the selection of Saffman–Taylor fingers with small surface tension, Euro. J. App. Math., 10(6) (1999), pp. 513–534.

[12]   S. J. Chapman and D. B. Mortimer, Exponential asymptotics and Stokes lines in a partial differential equation, Proc. Roy. Soc. Lond. A, 461 (2005), pp. 2385–2421.

[13]   S. J. Chapman and J.-M. Vanden-Broeck, Exponential asymptotics and capillary waves, SIAM J. Appl. Math., 62(6) (2002), pp. 1872–1898.

[14]   S. J. Chapman and J.-M. Vanden-Broeck, Exponential asymptotics and gravity waves, J. Fluid Mech., 567 (2006), pp. 299–326.

[15]   R. B. Dingle, Asymptotic Expansions: Their Derivation and Interpretation, Academic Press, New York, 1973.

[16]   J. Écalle, Les fonctions résurgentes:(en trois parties), volume 1, Université de Paris-Sud, Département de Mathématique, Bât, 425, 1981.

[17]   R. Grimshaw and N. Joshi, Weakly nonlocal solitary waves in a singularly perturbed Korteweg-de Vries equation, SIAM J. Appl. Math., 55(1) (1995), pp. 124–135.

[18]   C. J. Howls, P. J. Langman, and A. B. Olde Daalhuis, On the higher-order Stokes phenomenon, Proc. Roy. Soc. Lond. A, 460(2121) (2004), pp. 2285–2303.

[19]   M. D. Kruskal and H. Segur, Asymptotics beyond all orders in a model of crystal growth, Stud. Appl. Math., 85 (1991), pp. 129–181.

[20]   C. J. Lustri, Nanoptera and stokes curves in the 2-periodic Fermi–Pasta–Ulam–Tsingou equation, Physica D, 402 (2020), p. 132239.

[21]   C. J. Lustri and S. J. Chapman, Steady gravity waves due to a submerged source, J. Fluid Mech., 732 (2013), pp. 660–686.

[22]   C. J. Lustri, C. C. Green, and S. W. McCue, Selection of a Hele-Shaw bubble via exponential asymptotics, SIAM J. App. Math., 80(1) (2020), pp. 289–311.

[23]   C. J. Lustri and M. A. Porter, Nanoptera in a period-2 Toda chain, SIAM J. App. Dyn. Sys., 17(2) (2018), pp. 1182–1212.

[24]   G. G. Stokes, On the discontinuity of arbitrary constants which appear in divergent developments, Trans. Cam. Phil. Soc., 10 (1864), pp. 106–128.

[25]   P. H. Trinh, Exponential asymptotics and Stokes line smoothing for generalized solitary waves, In H. Steinrück, F. Pfeiffer, F. G. Rammerstorfer, J. Salençon, B. Schrefler, and P. Serafini, editors, Asymptotic Methods in Fluid Mechanics: Survey and Recent Advances, volume 523 of CISM Courses and Lectures, Springer Vienna, 2011, pp. 121–126.

[26]   A. Vainchtein, Y. Starosvetsky, J. D. Wright, and R. Perline, Solitary waves in diatomic chains, Phys. Rev. E, 93(4) (2016), p. 042210.

[27]   T.-S. Yang and T. R. Akylas, Weakly nonlocal gravity–capillary solitary waves, Physics of Fluids, 8(6) (1996), pp. 1506–1514.