I am currently a PhD student studying Mathematics at the University of Queensland (UQ) working on ergodic theory and dynamical systems. Since high school, my passion has always been towards Mathematics. After graduating high school I wanted to pursue Mathematics further. I went to the Jordan University of Science and Technology where I did my undergraduate called the Bachelor of Applied Mathematics. I appreciate the theory behind Mathematics and so I wanted to strengthen my knowledge after graduating. I felt studying a masters degree in the United States would expose me to new learning environments and provide me different opportunities to interact with people in the industry. Therefore, I attended Clemson University studying the Masters of Science in Mathematical Sciences. I wrote a thesis about localized frames and compact operators between Hillbert Spaces. My thesis initiated my interest in wanting to expand my thoughts. Therefore, alongside my supervisor Mishko Mitkovski who worked on Mathematical Analysis, my thesis was later published in the Journal of Fourier Analysis and Applications. While attending Clemson University I gave several talks and participated in several conferences at different Universities across the United States. During my Masters I took an interesting class on dynamical systems which motivated me to acquire my PhD and focus my future research in this area. I then began looking for supervisors globally who I believed would best help me achieve my goal. My best choice was working with Dr. Cecilia González-Tokman and I moved to Australia to begin a research based PhD at the University of Queensland.

During the last three years of my PhD, I was lucky to have met plenty of people working on dynamical systems and ergodic theory through departmental invited speakers. Presenting in the Sydney Dynamics Group (SDG) workshops and AustMS meetings was also a great experience and provided an access to meeting researchers from Australia, New Zealand and all the world. Many thanks to UQ, AustMS and my supervisor for providing all the support to attend these events.

Over the last ten years, I also served as a lecturer and a teaching assistant of Mathematics in six universities in four different countries where I taught, tutored and provided guidance to students from several faculties, including engineering, science and mathematics.

My research focuses on the ergodic theory of dynamical systems, in particular the so called random, time dependent, or non autonomous dynamical systems. Namely, given an \(X\subset \mathbb{R}^{n}\), \(n\geq1\) and a collection of maps \(\{f_{\omega}:X\circlearrowleft \}_{\omega\in\Omega}\) indexed by a probability space \((\Omega,\mathbb{P})\) where the randomness is governed by an external ergodic system \(\sigma :\Omega\circlearrowleft\). At each time \(\omega\in\Omega\), a map \(f_{\omega}\) is selected and applied to generate the next stage of the dynamics, instead of iterating the same map (deterministic case), see the graph in Figure 1. Random dynamical systems model more complex systems than deterministic systems and the relevance of these systems is clear due to the fact that systems are usually influenced by external factors or noise.

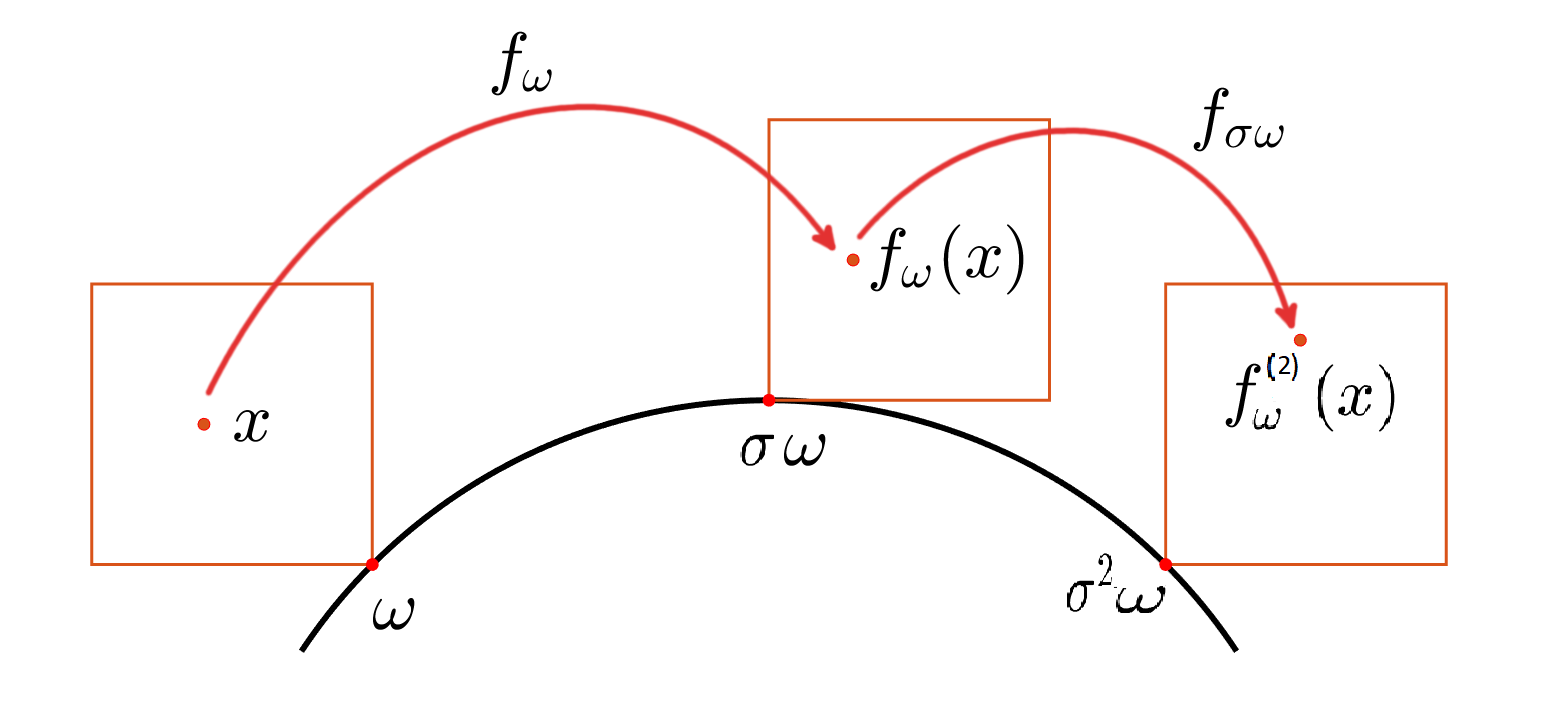
Figure 1. Random trajectory of \(x\) is \(f_{\omega}^{(k)}(x)=f_{\sigma^{k-1}\omega}\circ...\circ f_{\sigma\omega }\circ f_{\omega}(x)\).

A fundamental question in the ergodic theory of dynamical systems is to statistically understand the asymptotic or long term behavior of (random) trajectories defined by a (random) dynamical system. For this purpose, we attempt to understand and quantify the (random) invariant measures, particularly those with physical relevance. This problem has been intensively studied for several classes of one dimensional deterministic systems after the key initial paper by Lasota and Yorke [4] in 1973.

I mainly study the ergodic properties of certain classes of random higher dimensional systems (\(n\) is strictly bigger than one). We show the quasi-compactness, existence and bound the number of physical random invariant measures. This problem is still largely unsolved for many classes of higher dimensional systems. Among those who first studied random dynamical systems are, Ulam and von Neumann [9], Morita [6], Pelikan [7], and Buzzi [2].

Our approach relies on the so called transfer (or Perron Frobenius) operators, acting on higher dimensional function spaces such as functions of bounded variation [3] and Quasi-Hölder functions [8]. In higher dimensions, the situation is more challenging than in one dimension. For example, the choice of this function space and the geometry of the dynamical partitions are of crucial importance. For a nonsingular map \(f:X\circlearrowleft\), the transfer operator \(\mathcal{L}_{f}\) encodes information about the application of \(f\) and describes how densities evolve in time. This means if a collection of points in \(X\) is distributed according to a probability density \(h\), and the collection is pushed forward by \(f\), then the new collection of points will be distributed according to a new density denoted by \(\mathcal{L}_{f}h\).

For the next future work, I have ideas on using the well known Ulam's method to approximate the random invariant densities in [1]. Moreover, I am also interested in studying the random setting of Liverani [5].

I thank Dr. Robert Marangell for inviting me to write for the Dynamical Systems Web, Chantelle Blachut for helping me preparing the above graph, Dr. Cecilia González-Tokman and Abbi Howard for editing.

References

[1]   F. Batayneh and C. González-Tokman, On the number of invariant measures for random expanding maps in higher dimensions, ArXiv: 2102.13292.

[2]   J. Buzzi, Absolutely continuous SRB measures for random Lasota-Yorke maps, Transactions of the American Mathematical Society, 352.7, 2000, pp. 3289–3303.

[3]   E. Giusti, Minimal surfaces and functions of bounded variation, Birkhäuser, 1984.

[4]   A. Lasota and J. A. Yorke, On The Existence of invariant measures for piecewise monotonic transformations, Transactions of the American Mathematical Society, 1973, pp. 481–488.

[5]   C. Liverani, Multidimensional expanding maps with singularities: a pedestrian approach, Ergodic Theory and Dynamical Systems, 33.1, 2013, pp. 168–182.

[6]   T. Morita, Random iteration of one-dimensional transformations, Osaka Journal of Mathematics, 22.3, 1985, pp. 489–518.

[7]   S. Pelikan, Invariant densities for random maps of the interval, Transactions of the American Mathematical Society, 281.2, 1984, pp. 813–825.

[8]   B. Saussol, Absolutely continuous invariant measures for multidimensional expanding maps, Israel Journal of Mathematics, 116.1, 2000, pp. 223–248.

[9]   S. Ulam and J. von Neumann, Random ergodic theorem, Bulletin of the American Mathematical Society, 51, 1947.