I am a Mathematics PhD student at Drexel University working on stochastic homogenization of Fermi-Pasta-Ulam-Tsingou (FPUT) type systems with spatially varying properties. Problems that infuse randomness into classical systems interest me because the randomness may or may not affect the qualitative or quantitative phenomena in unexpected ways. One famous example where the effects of randomness cause an unexpected phenomenon is Anderson Localization [4]. This is due to the surprising fact that certain random Laplacians have entirely pure point spectra [2].

Research

In my work, I study the existence and behavior of propagating waves in the context of lattices composed of randomly varying springs and masses [5]. Stochastic homogenization is well-understood for continuous systems: possible approximate solutions are found by taking the rapidity of the spatially varying coefficient to infinity [3]. In the spatially discrete domain however, one must look for solutions in the long wave limit. In both fields, multiscale homogenization is used to derive effective equations. Homogenization allows one to use the large length of the wave to average over large swaths of the lattice at once. One would then suspect that by the strong law of large numbers, such an average would approach a statistical mean. The real work is in trying to analytically prove that the effective equations are valid, and if they are, to what degree and for what time scales do the solutions to the effective equations approximate solutions to the system. My advisor, J. Douglas Wright, who had proven the existence of approximate-soliton solutions for very long time scales in the periodic case [7], wanted to see if something similar happened in the random case, which is how the project began.

Figure 1. One-dimensional infinite spring-mass system with spatially varying masses and springs.

The basic form of the equation I study is

\(m(j)\ddot{u}(j)=k(j)[u(j+1,t)-u(j,t)]+k(j-1)[u(j,t)-u(j-1,t)]\)

(1)

where the coefficients \(m(j)\), the "masses", and \(k(j)\), the "springs", are random. The equation can be derived from the forces acting on an infinite spring-mass system as in Figure 1, or from the electrodynamics of an infinite LC circuit [1] if the \(k(j)\) are taken to be constant. Respectively, \(u(j)\) is the position of the \(j\)th mass or the voltage of the \(j\)th capacitor. What we have been able to prove so far is that in the one-dimensional setting, when the masses and springs are i.i.d., solutions to (1) can be approximated well by solutions to the wave equation with wave speed \(c=\sqrt{\dfrac{\tilde{k}}{\bar{m}}}\) up to times proportional to the wavelength. This, unlike Anderson localization, is expected, literally, since \(\dfrac{1}{\tilde{k}}=\mathbb{E}\left[\dfrac{1}{k(j)}\right]\) and \(\bar{m}=\mathbb{E}[m(j)]\), but also figuratively because it mirrors results in the more studied continuous world of PDEs. In our argument we prove two types of approximations, both of which depend on the analysis of random walks.

Approximating FPUT by the wave equation

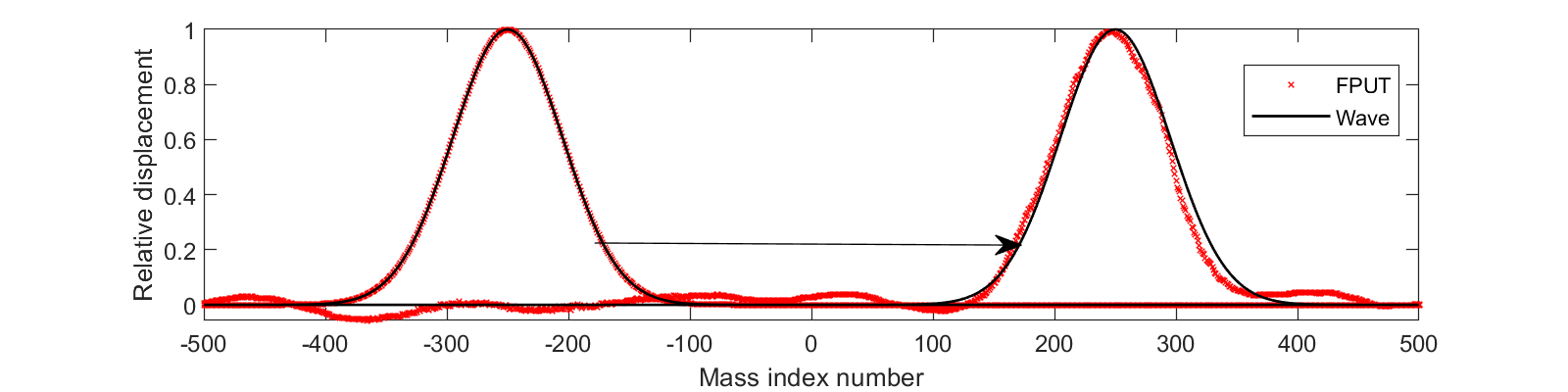
Figure 2. The wave and FPUT with randomly chosen masses are shown both at initial positions and at a time that is not much longer than the wavelength.

The first approximation is valid with probability one and hinges upon the classical result known as the law of iterated logs. The law of iterated logs is a very sharp description of random walks. It gives us a boundary for which the magnitude of a random walk is larger only finitely many times. However, the magnitude of a random walk approaches the boundary from below infinitely many times. The only problem with this approach is that, although one can say the approximation gets better as the wavelength gets larger, one really has no idea how good the approximation is for a fixed wavelength. This is due to the fact that a random walk crosses the boundary a finite number of times which could, in principle, still be a big number. The second approximation is an approximation in mean and requires the use of maximal inequalities. It complements the first result by giving concrete estimates on how good the approximation is, in terms of standard deviations. This allows us to say that smaller standard deviations of the random coefficients allow for better approximations. Figure 2 gives a visual idea of just how good this approximation is. The result is both intuitive and rigorous, and we think all but sharp.

Attenuation over extremely long time

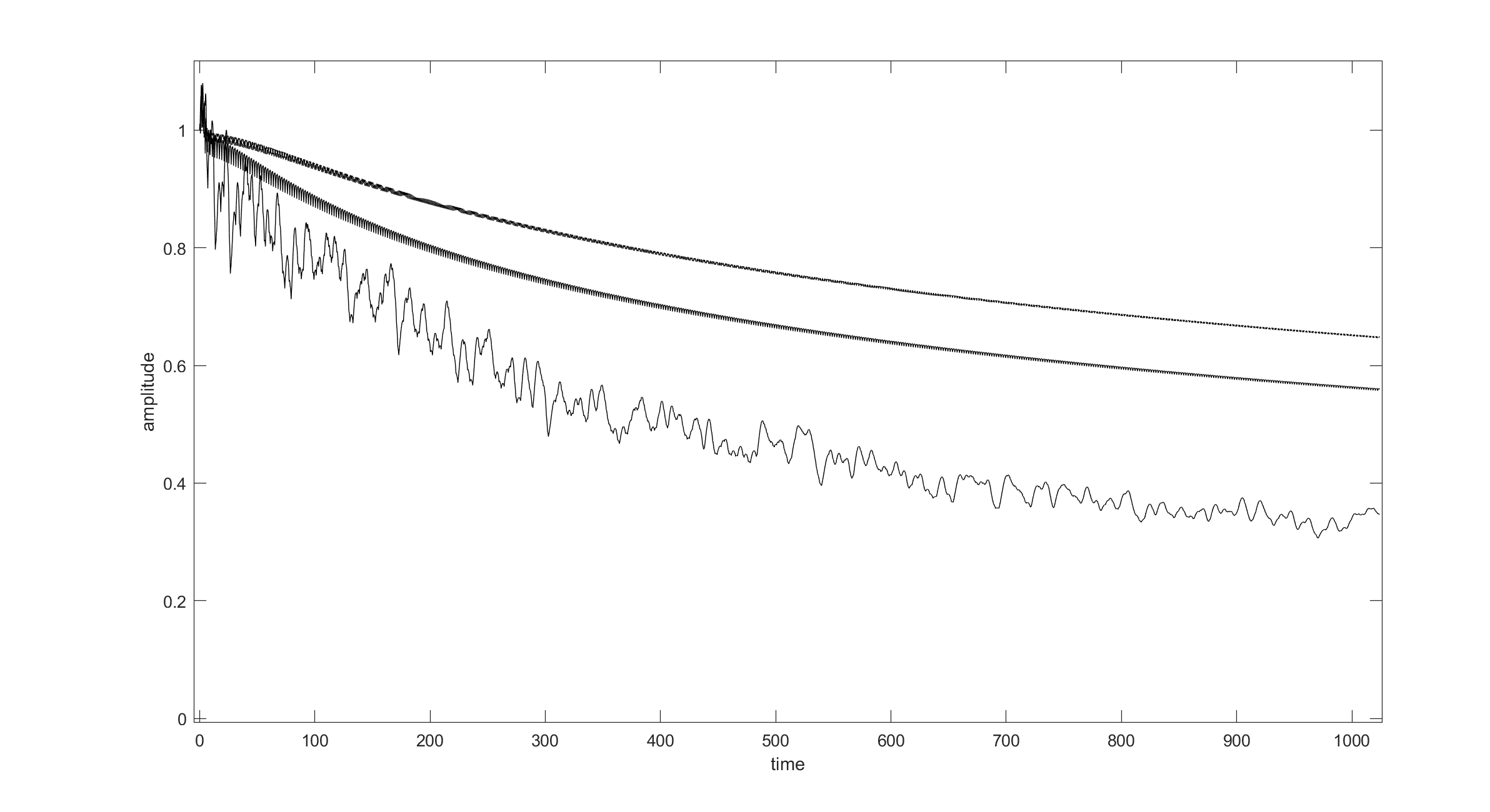
Figure 3. From top to bottom we see the wave amplitude for constant mass, periodic mass, and random mass configurations. The final time is orders of magnitude larger than the wavelength.

In the remaining time I have left at Drexel, I aim to generalize our first result to arbitrary dimensions, which I already have an idea about how to do. The tactic is not so simple as in one-dimension, but results have already been proven for the periodic case [6]. Then, after having established a rigorous foundation for the existence of traveling waves on such systems, I would like to study traveling waves over larger time scales. For example, could one approximate the distribution of true solutions for longer times by the law of a traveling wave with an amplitude or speed that is a random variable? In addition to that, I would like to quantify, or at least rigorously justify, the apparent faster attenuation, see Figure 3, and perhaps even localization of the solutions that one sees in the case of random coefficients. Finally, it would be interesting to see if the technique could work on other similar lattice systems.

Everything else

Outside of my research, I enjoy playing ultimate frisbee, reading fiction, and learning about science. I am an avid piano player, having played since I was 5. Bebop is my favorite genre to play, but my cat purr-furs when I play smooth jazz.

References

[1]   H. S. Bhat and B. Osting, Diffraction on a the Two-dimensional Square Lattice, Siam J. of Appl. Math., 70, (2009), pp. 1389–1406.

[2]   K. E. Bessing, Spectral Properties and Localization of Two Random Laplacians on Graphs, Ph.D. thesis, The University of Alabama, Birmingham, Alabama, 2015.

[3]   D. Cioranescu and P. Donato, An Introduction to Homogenization, Oxford Lecture Ser. Math. Appl. 17, The Clarendon Press, Oxford University Press, New York, 1999.

[4]   D. Hundertmark, A short introduction to Anderson localization, 2007, https://faculty.math.illinois.edu/~dirk/preprints/localization3.pdf (accessed 2021-04-02).

[5]   J. A. McGinnis and J. D. Wright, Using Random Walks to Establish Wavelike Behavior in an FPUT System with Random Coefficients, Apr. 2021, https://arxiv.org/abs/2104.00463.

[6]   A. Mielke, Macroscopic Behavior of Microscopic Oscillations in Harmonic Lattices via Wigner-Husimi Transforms, Arch. Rational Mech.Anal., 181, (2006), pp. 401–448.

[7]   J. Gaison, S. Moskow, J. D. Wright, and Q. Zhang, Approximation of Polyatomic FPU Lattices by KdV Equations, Mult. Scale Model. Simul., 12 (2014), pp. 953–995.