1. Introduction

I am Xie He, a third-year Ph.D. student in Mathematics at Dartmouth College, advised by Dr. Peter J. Mucha. I obtained my bachelor degree in Applied Mathematics at University of California, Los Angeles in 2019. My main research interests are in network science and multilayer networks. My interest in networks dates back to my undergraduate days at UCLA where I took my first course in networks with Dr. Mason A. Porter. The ubiquitous and fascinating application of graphs immediately captured my attention. I knew by then I wanted to pursue a degree related to dynamical systems, specifically in graph related problems. In the summers of 2018 and 2019, I conducted research at the UCLA REU with Dr. Andrea L. Bertozzi and her awesome research team. During this period, I mainly worked on subgraph matching problems. The problem focused on finding a small template graph in a large multilayer network. We proposed a filtering algorithm for exact subgraph matching and an A* search algorithm for noisy subgraph matching. Our results have been published and have many potential interesting applications.

2. Research

My current research in network science mainly focuses on sampling network edges and link prediction on both static and temporal networks. Links are also known as edges in networks. The nodes and the links that connect them are the most important things in a network. When nodes represent people in a social network, edges/links represent the connection between these people. The go-to example I like to use is Facebook. Imagine you are friends with someone on Facebook: then you would be connected to them through an edge/link. Thus, edges could be used to represent friendships in social networks as well as protein-protein interactions in biological networks and traffic flow in transportation networks.

In short, edges define the network and its topology. But networks are dynamical systems and the ways in which they change over time are particularly fascinating to me. Temporal networks and their link changes are very important in the study of network science.

Real-world networks are often incomplete for a variety of reasons, such as missing relations in social networks, inherent noise in biological networks, and specific user privacy limitations in wireless networks. To compensate for this issue, many link prediction algorithms have been purposed in different disciplines. Among various methods of link prediction, well-studied topological features are widely used for prediction on static networks. Many efforts have been made by network scientists in this field including common neighbors and clustering coefficient for social networks; Katz centrality and resource allocation for electrical power grid and protein–protein interaction networks; and local path index for airport transportation networks. Furthermore, recently it has been shown the stacking of static topological features could produce near-optimal results for static networks [1].

However, most real-world networks and their topological structure evolve dynamically over time, considering the dynamical properties in real-world networks, temporal link predictions have many applications, including recommendation systems on social media and predictions of brain activity. Various approaches have been applied to temporal link prediction problems, however, few have considered using temporal topological features in temporal link prediction. Objectively, temporal topological features need a considerable amount of additional feature engineering, and computing them requires quite a lot of resources. However, avoiding temporal topological features could lead to potential biased outcomes. Thus, it is crucial to understand if the cost of using temporal topological features is worth the improvement they provide in temporal link prediction tasks.

To this end, we introduced 41 stacked temporal topological features and extended the single-layer stacking in [1] to construct a temporal stacking link prediction algorithm (shown in Figure 1).

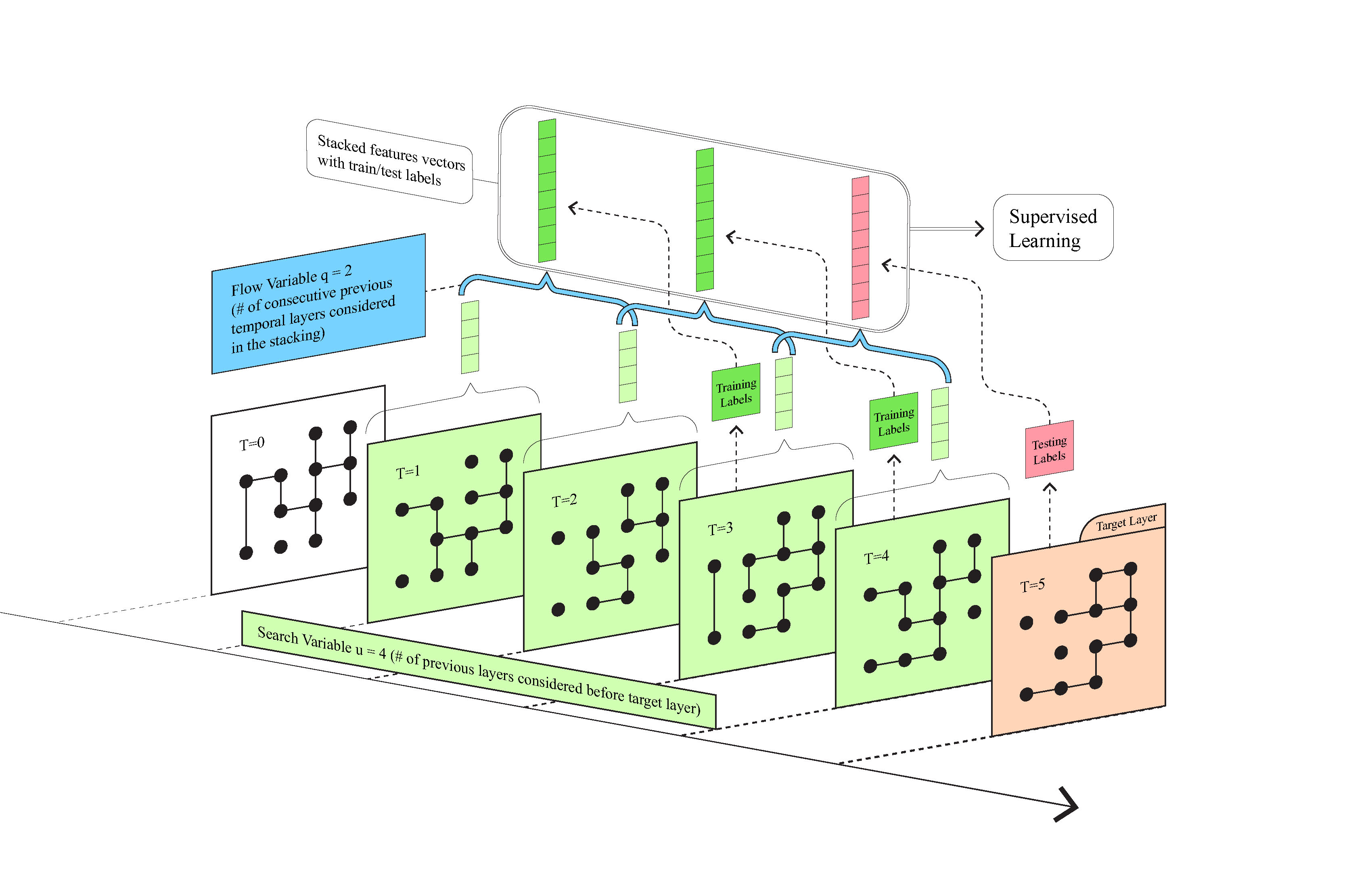
Figure 1: A diagrammatic explanation of the temporal stacking algorithm for link prediction. We consider consecutive temporal layers with the flow variable \(q\) (blue, \(=2\) in the toy model visualized here) setting the number of consecutive layers used in a stacked feature vector and search variable \(u\) (green, here \(=4\)) setting the total number of layers before the target used to train the prediction. Features are generated for sampled dyads and stacked across \(q\) neighboring layers, with the following layer providing the labels (green for training and red for testing). We then use supervised learning to generate the predicted result and analyze performance.

Missing link predictions on static network usually assume a partial missing from an observed single-layer network, and use the rest of the network to complete the prediction. The general setting for temporal link prediction is different from missing link prediction for static networks. There are generally two different settings for temporal network link predictions. Our method could be applied to both cases. The basic setup for both setting are the same. First, we define a temporal network \(G = \{G_{0}, \ldots, G_{T+1}\}\) to contain temporal layers \(G_i = (V_i,E_i)\), where \(i\) represents the \(i\)th time slot in which the connection happened, \(V_i\) and \(E_i\) contain the set of nodes and edges that appeared in the \(i\)th time slot, respectively. In a similar way, we define the node set \(V = \{V_0, \ldots, V_{T+1}\}\) and the edge set \(E = \{E_0, \ldots, E_{T+1}\}\) to contain all layers' nodes and edges respectively. Across the different temporal layers, we assume that we know every node appeared in the temporal network, i.e. we assume the node set \(V\) is given from \(i=0\) to \(i=T+1\). The layer \(G_{T+1}\) is considered the target layer in the temporal link prediction, i.e. we want to predict the edges in \(G_{T+1}\).

The first setting is somewhat similar to the setting of static network link prediction. We assume that the target layer \(G_{T+1}\) is partially observed, which is called \(G_{T+1}^{O}\). The unobserved portion is referred to as \(G_{T+1}^{UN}\), and we use the information from temporal layers available from \(G_{0}\) to \(G_{T}\) plus \(G_{T+1}^{O}\) to predict the missing edges in \(G_{T+1}^{UN}\).

The second setting assumes the edge set \(E_{T+1}\) in the entire target layer \(G_{T+1}\) is missing. We are then given the information from \(G_{0}\) to \(G_{T}\) to predict the edges in the target layer \(G_{T+1}\).

Temporal dependency is a very important aspect of temporal networks, however, one would not want to use outdated news from hundreds of years ago to predict the current trend. To avoid this, we set a search variable \(u\) to determine how far back along time we would like to search for the useful information. Another aspect of temporal networks is their flow along the time. For instance, every three months could be considered a cycle . To capture this flow of information, we set a flow variable \(q\) to determine how many consecutive temporal layers we want to consider in the stacking of features across time (see Figure 1). We then apply supervised learning to train a model, with \(u-q\) being the number of training groups, while using area under the curve (AUC) to evaluate prediction accuracy. Note that the search variable \(u\) and the flow variable \(q\) are free to adjust according to different experiment settings and application purposes.

By comparing the prediction results from several different temporal topological features and stacked temporal topological features, we demonstrate the stacked features could achieve similar or even better results in temporal link prediction tasks than temporal features. Empirically, the stacking of features is also much less expensive than direct calculation of temporal features computationally. Therefore, we avoid the verbose definition and the cumbersome computational cost of temporal topological features. A preprint detailing these methods is forthcoming.

In my remaining time at Dartmouth, I aim to find the relationship between results of different link prediction methods and different sampling methods. Though uniform sampling is often applied in most cases, one could wonder if we change our ways of sampling of the edges, will the result change much in the prediction.

I thank Mason who introduced me to network science, for being a wonderful scientist and awesome mentor, and for inviting me to write this article. I also thank Peter not only for all the kindness and guidance I have received during my studies in network science, but for being a wonderful mathematician and advisor.

3. Other than Research

In case you were wondering, my first name is pronounced "Shae." I have been to 25 national parks in the US and am currently adding to that list; I write novels on AO3; I love gothic lolita and have a black cat Sesame who brings me good luck.

References

[1]   Amir Ghasemian, Homa Hosseinmardi, Aram Galstyan, Edoardo M. Airoldi, and Aaron Clauset, Stacking models for nearly optimal link prediction in complex networks, Proceedings of the National Academy of Sciences, 117(38), 2020, pp. 23393-23400.