This article is a reproduction of the two articles: My Lunch with Arnol'd by Gábor Domokos, and Mono-monostatic bodies: The answer to Arnol'd's question by Péter Várkonyi and Gábor Domokos
The Mathematical Intelligencer 28(4) (2006), pages 31-33 and 34-38 © Springer-Verlag; with kind permission of Springer Science and Business Media.

My Lunch with Arnol'd

by Gábor Domokos

I thank Jim Papadopoulos for the pre-Arnol'd version of the problem described here and Andy Ruina for encouraging me to write this story down and then editing it.

In Hungary I teach Civil Engineering. I lean more towards the mathematical side of the subject than to designing buildings. Just after the political changes swept over the country in the late 1980s I got a Fulbright Fellowship to visit America, to an engineering department known to have people with mathematical tastes like mine. I had a good year writing papers with various American Professors. One of them was Andy Ruina, with whom I became friends and had an infinite number of conversations on not quite as many topics. One recurrent theme was Andy's friend Jim Papadopoulos, a guy with academic taste but not an academic job. Through Andy I respected the unseen Jim.

One day Andy told me that Jim had a simple conjecture, but that Jim was too busy with his day job, designing machines to refill laser toner cartridges, to work on trying to prove it. Jim offered through Andy, as a gift of sorts, that I could work on the problem.

Jim imagined drawing a closed curve on a thick piece of plywood. A convex curve, meaning that it had no indented places. A circle, an ellipse and a rectangle are convex curves and a heart-shape is not. Now cut along that line with a jigsaw and balance the plywood piece, on edge, on a flat table. Gently keep it on edge so it doesn't fall flat on the table. In mathematical language, think of this as a two-dimensional (2D) problem. This plywood is only stable in certain positions. For example a square piece of plywood is stable on all four edges. In the positions where one diagonal or the other is vertical the plywood is in equilibrium, but it is an unstable equilibrium. A tiny push and it will fall towards lying on one of the edges. An ellipse is in stable equilibrium when horizontal and resting on one of the two flatter parts. And the same ellipse is in unstable equilibrium when balanced on either end, like an upright egg. Jim conjectured that no matter what convex shape you draw and cut out, it has at least two orientations where it is stable. The ellipse has two such positions, a triangle has three (the three flat edges), a square has four, a regular polygon has as many stable equilibrium positions as it has edges. And a circle is a degenerate special case that is in equilibrium in every orientation (none of which are stable or unstable). Jim's conjecture was that every shape, but for a circle, has at least as many stable positions as an ellipse has: two.

Jim's plywood conjecture was a simple idea, and it was true for every shape we could think of. Of course it is not true if you are allowed to add weights. For example, you can put a big weight in a plywood ellipse near one of the sharp ends, so the only stable configuration is standing upright, like a child's toy called the 'comeback kid'. We didn't allow that. We only allowed homogeneous shapes, uniform plywood.

After some days of thought and talk with Andy, Jim and others, we found a proof that showed that every convex piece of plywood has at least two orientations where it would stand stably. Then we generalized the idea to include things made from wire. We published the results in the respectable but not widely read Journal of Elasticity.

What kept bugging us was the 3D generalization. Imagine something made of solidified clay. Was it true that you could always find at least two orientations for such a thing where it would sit stably on a table? We couldn't prove this, and for good reason. Finally I found a counterexample; I found a shape that could only balance stably on a table in just one position. Take a long solid cylinder and diagonally chop off one end, then at the opposite angle chop off the other end. This truncated cylinder is happy lying on the table with its long side down, but in no other position. Just one stable equilibrium. We never published this and I stopped thinking about balancing plywood shapes, wire loops and clay solids.

About 5 years later there was the International Congress on Industrial and Applied Mathematics in Hamburg. This was to be the biggest mathematics meeting ever with over 2000 people attending. Coming from a second-world country I needed, applied for, and got a little first-world money so I could attend. The meeting had over 40 parallel sessions. At any one time of the day I had a choice of over 40 different talks I could listen to. My own talk was on something I thought was profound at that time. But it was put in the wrong session. To an outsider math might seem like math. But either the subject is broad or mathematicians are narrow; the number of talks that any single conference attendee could hope to understand was small. Although my audience sat politely through my carefully practiced 15-minute presentation, I don't think any of the few who understood my English understood a word of my mathematics. Mine seems not to have been the only misplaced talk, I didn't understand any of the talks I went to either. Besides thousands of these incomprehensible 15-minute talks there were three simultaneous 45-minute long invited talks each day.

Most centrally, there was one plenary talk with no simultaneous sessions. All 2000 mathematicians could attend without conflict. This plenary lecture was to be presented by no less than Vladimir Igorevich Arnol'd, the man who solved Hilbert's thirteenth problem when he was a teenager and the author of countless famous articles, reviews, books and theorems.

Like everyone else I felt obligated to go despite, again like everyone else, having little hope of understanding anything of this great man's work. There was a general steady murmur as Arnol'd started his talk; people chatting to their friends whom they understood rather than listening to Arnol'd whom they had no hope of understanding. When a talk is over my head I either switch off completely, as I did for most of the conference talks, or try to catch a detail here or there that might fit together loosely in my mind somehow. I did the latter until my breath was taken away. Arnold's talk made excursions into various topics that I don't know about, like differential geometry and optics. But each topic ended with something about the number four. He said these topics were examples of a theorem created by the great nineteenth-century mathematician Jacobi. He said Jacobi's theorem had many applications, and that always something had to be bigger or equal to four. He covered one topic or another that would be familiar to each person in the audience, always coming back to the number four. After everyone in the audience had seen the number four appear in some problem that he knew something about, the murmers of distracted conversation quieted. The giant auditorium became next to silent, with people practically holding their breaths in attentiveness. Four in this problem, four in that, four in some problem or other that everyone could understand. Four, four, four. My respect for Arnol'd grew. Being a brilliant mathematician is one thing. Riveting 2000 mathematicians who mostly can't understand each other is another. Although I didn't understand the lecture, I felt exhilarated and happy. As I left the auditorium it suddenly struck me that Jim's plywood and wire problem might be related to Jacobi's theorem. We had proved that at least two stable equilibria existed, but this implies that there are at least four equilibria, two stable and two unstable. Like the ellipse. Arnold's four. I was so impressed with myself that I stopped dead for a minute, blocking the exit.

I had to tell this to Arnol'd. Maybe the number four was a coincidence, maybe not. He would know. But of course Arnol'd was mobbed after the talk. I realized that getting face to face with the great man might be impossible. But almost immediately I noticed a big poster. The conference organizers were advertising special lunches. For an exorbitant fee one could buy a ticket to eat with a math celebrity. Although my budget was tight and my mathematics is not at the level of Arnol'd, I could calculate that if I reduced my eating from two hotdogs a day to one I could afford a lunch ticket with the great Professor.

The lunch was a disaster, both from my point of view and Arnold's. The organizers had tried to maximize their profit rather than the ticket-buyers' pleasure. At the big round table with Arnol'd were ten eager young mathematicians. Each was carrying one or two 'highly important' scientific papers which were full of 'highly relevant' results which they wanted to share with Arnol'd. He could not eat as they held out their papers and made claims about their great original contributions. And unless I was willing to butt into this noisy whining, like each of the people was doing to the others, I could not speak. I sat and tried to look attentive at the pathetic scene. At the end of the meal Arnol'd finally asked me "And what is your paper about?" I said "nothing." "Surely you have something to ask or say" he said. But I was depressed by the fray and said no, I had just wanted to listen. The big meeting went on day after day. I ate one hotdog a day and I went to a hundred 15-minute talks that I didn't understand.

On the last day I packed my suitcase and headed for the airport. The main lobby of the conference center was deserted, maintenance people were taking down posters, the buffet was closed, people were fading out. As I strolled across the big hall I noticed, next to a young Asian man, leaning on a counter near the closed buffet, Professor V.I. Arnol'd. The young Asian man was talking excitedly in the tone I had seen at the disastrous lunch. As I walked closer, Arnol'd raised his voice slightly.

"As I told you already several times, there is nothing new in what you are telling me. I published this in 1980. Look it up. I do not want to discuss this further; moreover, I have an appointment with the gentleman carrying the suitcase over there. Good bye."

The disappointed Asian mathematician got up to leave and Arnol'd turned to me. "You wanted to talk to me, right?" Stunned that he even remembered me, but aware of the part I suddenly was supposed to play, I pretended that the discussion was expected. "You sat at the lunch table, right? You must have had a reason. What is it about? Tell me fast. I have to catch my train."

We sat down, I collected my thoughts and explained about the plywood and the wire and how they gave the number two which really meant four. He stared off without saying a word. After five minutes I asked him if he wanted to know how we proved that the plywood had at least four equilibria. He waved me away impatiently. "Of course I know how you proved it" and then breezily outlined the proof in a few phrases. "That is not what I am thinking about. The question is whether your result follows from the Jacobi theorem not."

He stared off again. I reminded him of his train but he waved me away again. Looking at his enormous concentration, and not knowing what I should be thinking about, the minutes went by slowly. Finally he said "I think the Jacobi theorem and your problem are related, but yours is certainly not an example of the other. I think there is a third theorem that includes both Jacobi's theorem and your problem. I could tell better if I knew about the 3D version of your problem."

I proudly described the counterexample, the single stable equilibrium of the chopped-off cylinder but he cut me off:

"You realize of course that this is not a counterexample! The main point of your 2D result was NOT to show that there are two or more stable equilibria, but to show that there are FOUR or more equilibria altogether." This was not the main point of our 2D result in my mind, or at least hadn't been. But now I realized that there was a higher level of thought going on here. Four and not two. "And your cylinder has four equilibria, three of which are unstable."

In a moment's pondering I realized he was right. The cylinder could also balance unstably when rotated 180 degrees on its axis and also on its two ends. Four. I was stunned. "A counterexample may still exist. Send me when you found a body with less than four equilibria in the three-dimensional case" he said, "I have to catch my train. Good bye young man, and good luck to you!"

I returned to Hungary and my life of teaching and pretty little irrelevant problems, each important in my mind for a few months or years. It is possible that, besides the proofreader at the Journal of Elasticity, no-one's eyes have ever passed at all over our paper on plywood and wire. Ten years later Arnold's conjecture turned out to be correct --- the three-dimensional counterexample not only existed but appeared to me as a mathematically most exciting object. I never saw Arnol'd again. Besides the number four, and four again, I still have no idea what the Jacobi theorem is about. So I will never understand the generalization of Jacobi's theorem that V.I. Arnol'd cooked up in order to encompass our balancing plywood and wire, cooked up there in the huge convention hall in Hamburg, Germany, sitting next to me at the deserted buffet.

 

Mono-monostatic bodies: The answer to Arnol'd's question

P. L. Várkonyi and G. Domokos
Budapest University of Technology and Economics
Department of Mechanics, Materials and Structures and Center for Applied Mathematics and Computational Physics

Abstract

V.I. Arnol'd conjectured that convex, homogeneous bodies with less than four equilibria (also called mono-monostatic) may exist. Not only turned his conjecture out to be true, the newly discovered objects show various interesting features. Our goal is to give an overview of these findings based on [12] as well as to present some new results. We will point out that mono-monostatic bodies are neither flat, nor thin, they are not similar to typical objects with more equilibria and they are hard to approximate by polyhedra. Despite these 'negative' traits, there seems to be strong indication that these forms appear in Nature due to their special mechanical properties.

1.   Do mono-monostatic bodies exist?

In his recent book [2] V.I. Arnol'd presented a rich collection of problems sampled from his famous Moscow seminars. As Tabachnikov points out in his lively review [11], one of the central themes concern the geometrical and topological generalizations of the classical Four Vertex Theorem [3], stating that a plane curve has at least four extrema of curvature. The condition that some integer is at least four appears in numerous different problems in the book, in areas ranging from optics to mechanics. Being one of Arnold's long-term research interests, this was the central theme to his plenary lecture in 1995, Hamburg, at the International Conference on Industrial and Applied Mathematics, presented to more than 2000 mathematicians. The number of equilibria of homogeneous, rigid bodies offers a big temptation to believe in yet another emerging example of being at least four (in fact, the planar case was proven to be an example [7]). Arnol'd resisted and conjectured that, counter to everyday intuition and experience, the three-dimensional case might be an exception. In other terms, he suggested that convex, homogeneous bodies with less than four equilibria (also called mono-monostatic) may exist. As often before, his conjecture not only proved to be correct, it opened up an interesting avenue of mathematical thought coupled with physical and biological applications, which we explore below.

2.   Why are they special?

We consider bodies resting on a horizontal surface, in the presence of uniform gravity. Such bodies with just one stable equilibrium are called monostatic and they appear to be of special interest. It is easy to construct a monostatic body, such as a popular children's toy called 'comeback kid'; see Figure 1(A). However, if we look for homogeneous, convex monostatic bodies, the task is much more difficult. In fact, in the 2D case one can prove [7] that among planar (slab-like) objects rolling along their circumference no monostatic bodies exist. (This statement is equivalent to the famous Four-Vertex theorem [3] in differential geometry.)

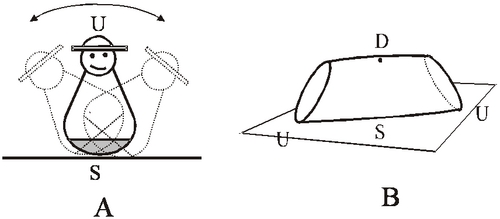Figure 1: A: Children's toy with one stable and one unstable equilibrium: inhomogeneous, mono-monostatic body), also called the 'comeback kid'. B: Convex, homogeneous solid body with one stable equilibrium (monostatic body). In both plots, S, D and U denote points of the surface corresponding to stable, saddle type and unstable equilibria of the bodies, respectively.

The proof for the 2D case is indirect and runs as follows. Consider a convex, homogenous planar 'body' B and a polar coordinate system with origin at the center of gravity of B. Let the continuous function R(φ) denote the boundary of B. As demonstrated in [7], non-degenerated stable/unstable equilibria of the body correspond to local minima/maxima of R(φ). Assume that R(φ) has only one local maximum and one local minimum. In this case there exists exactly one value φ = φ₀ for which R(φ₀ ) = R(φ₀ + π), moreover, R(φ) > R(φ₀ ) if π > φ - φ₀ > 0, and R(φ) < R(φ₀ ) if < π < φ - φ₀ < 0; see Figure 2(A). The straight line φ = φ₀ (identical to φ = φ₀ + π) passing through the origin O cuts B into a 'thin' (R(φ) < R(φ₀ )) and a 'thick' (R(φ) > R(φ₀ )) part. This implies that O cannot be the center of gravity, i.e., it contradicts the initial assumption.

Not surprisingly, the 3D case is more complex. Although one can construct a homogeneous, convex monostatic body (cf. Figure 1(B)), the task is far less trivial if we look for a monostatic polyhedron with a minimal number of faces. Conway and Guy [4] constructed such a polyhedron with 19 faces (similar to the body in Figure 1(B)); it is still believed that this is the minimal number. It was shown by Heppes [9] that no homogeneous, monostatic tetrahedron exists. However, Dawson [5] showed that homogeneous, monostatic simplices exist in d = 10 dimensions. More recently, Dawson and Finbow [6] showed the existence of monostatic tetrahedra, however, with inhomogeneous mass density.

One can construct a rather transparent classification scheme for bodies exclusively with non-degenerate balance points, based on the number and type of their equilibria. In 2D, stable and unstable equilibria always occur in pairs, so we say that a body belongs to class {i} (i > 0) if it has exactly S = i stable (and thus, U = i unstable) equilibria. As we showed above, class {1} is empty. In 3D we appeal to the Poincaré-Hopf Theorem [1] stating for convex bodies that S + U - D = 2, S, U, D denoting the number of local minima, maxima, and saddles of the body's potential energy, so class {i,j} (i, j > 0) contains all bodies with S = i stable, U = j 'unstable' and D = i + j - 2 saddle-type equilibria.

Monostatic bodies are in classes {1,j}; we will refer to the even more special class {1,1} with just one stable and one unstable equilibrium as mono-monostatic. While in 2D being monostatic implies being mono-monostatic (and vice versa), the 3D case is more complicated: a monostatic body could have, in principle, any number of unstable equilibria (e.g., the body in Figure 1(B) belongs to class {1,2} and has four equilibria altogether, as pointed out by Arnol'd). Arnold's conjecture was that class {1,1} is not empty, i.e., homogeneous, convex mono-monostatic bodies exist. Before we outline the construction of such an object we want to highlight its very special relation to other convex bodies.

Intuitively it seems to be clear that by applying small, local perturbations to a surface, one may produce additional local maxima and minima (close to existing ones), similar to the 'egg of Columbus'. According to some accounts, Christopher Columbus attended a dinner, which a Spanish gentleman had given in his honor. Columbus asked the gentlemen in attendance to make an egg stand on one end. After the gentlemen successively tried to and failed, they stated that it was impossible. Columbus then placed the egg's small end on the table, breaking the shell a bit, so that it could stand upright. Columbus then stated that it was "the simplest thing in the world. Anybody can do it, after he has been shown how!" In [12] we showed, in an analogous manner, that one can add stable and unstable equilibria one by one by locally taking away small portions of the body. Apparently, the inverse is not possible, i.e., for a typical body one can not decrease the number of equilibria via small perturbations.

This result indicates the special status of mono-monostatic bodies among other objects. For any given typical mono-monostatic body one can find bodies in an arbitrary class {i,j} which have almost the same shape. On the other hand, to any typical member of class {i,j} (i, j > 1), one cannot find a mono-monostatic body that has almost the same shape. This may explain why mono-monostatic bodies do not occur often in Nature, and also why it is difficult to visualize such a shape. Next we will demonstrate such an object.

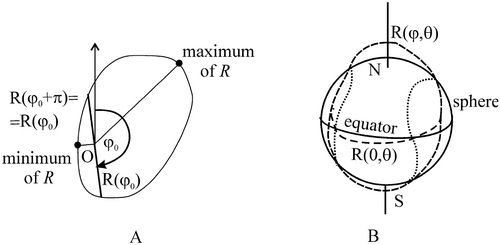Figure 2: A: Example of a convex, homogenous, planar body bounded by R(φ) (polar distance from the origin O). Assuming R(φ) has only two local extrema, the body can be cut to a 'thin' and a 'thick' half by the line φ = φ0 . Its center of gravity is on the 'thick' side, in particular, it cannot coincide with O, so we have contradiction. B: 3D body (dashed line) separated into a 'thin' and a 'thick' part by a tennis ball-like space curve C (dotted line) along which R = R0 . Continuous line shows a sphere of radius R0 , which also contains the curve C.

3.   What are they like?

Similar to the planar case, a mono-monostatic 3D body can be cut to a 'thin' and a 'thick' part by a closed curve on its boundary, along which R( θ, φ) is constant. If this separatrix curve happens to be planar, its existence leads to contradiction, similar to the 2D case. (If, for example, it is the 'equator' φ = 0 and φ > 0/φ < 0 are the thick/thin halves, the center of gravity should be on the upper (φ > 0) side of the origin). However, in case of a generic, spatial separatrix the above argument does not apply anymore. In particular, the curve can be similar to the ones on the surfaces of tennis balls; see Figure 2(B). In this case the 'upper' thick ('lower' thin) part is partially below (above) the equator, thus it is possible to have the center of gravity at the origin. Our construction will be of this type. We define a suitable two-parameter family of surfaces R( θ, φ, c, d) in the spherical coordinate system (r, θ, φ) with -π/2 < φ < π/2 and 0 < θ < 2π, or φ = ±π/2 and no θ-coordinate, while c > 0 and 0 < d < 1 are parameters. Conveniently, R can be decomposed in the following way:

R( θ, φ, c, d) = 1 + d ΔR( θ, φ, c),

(1)

where ΔR denotes the type of deviation from the unit sphere. 'Thin'/'thick' parts of the body are characterized by negativeness/positiveness of ΔR (i.e., the separatrix between the thick and thin portions will be given by ΔR = 0), while the parameter d is a measure of how far the surface is to the sphere. We will choose adequately small values of d to make the surface convex. Now we proceed to define ΔR.

We will have the maximum/minimum points of ΔR (ΔR = ±1) at the North/South Pole (φ = ±π/2). The shapes of the thick and thin portions of the body are controlled by the parameter c: for \(c \gg 1\) the separatrix will approach the equator, for smaller values of c the separatrix will become similar to the curve on the tennis ball.

Consider the following smooth, one-parameter mapping \(f(\varphi, c): (-\pi/2, \pi/2) \to (-\pi/2, \pi/2)\):

(2)

For large values of the parameter (\(c \gg 1\)), this mapping is almost the identity, however, if c is close to 0, there is a large deviation from linearity. Based on (2), we define the related maps

f1( φ, c) = sin( f( φ, c))

(3)

and

f2( φ, c) = -f1( -φ, c).

(4)

These two functions are used to obtain ΔR( θ, φ, c) = f₁( φ, c) if θ = 0 or π (i.e., a big portion of these sections of the body lie in the thin part; cf. Figure 2(B)) and ΔR = f₂ if θ = π/2 or 3π/2 (the majority of these sections are in the thick part). The function

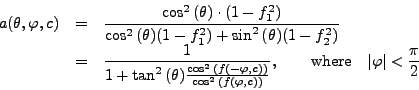(5)

is used to construct ΔR as a `weighted average' type function of f₁ and f₂ in the following way:

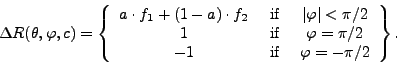(6)

The choice of the function a guarantees, on one hand, the gradual transition from ƒ1 to ƒ2 if θ is varied between 0 and π/2, on the other hand, it was chosen to result in the desired shape of thick/thin halves of the body; this is illustrated in Figure 2(B). The function R defined by equations (1)-(6) is illustrated in Figure 3 for intermediate values of c and d. For \(c \gg 1\), the constructed surface R = 1 + d ΔR is separated by the φ = 0 equator into two unequal halves: the upper (φ > 0) half is `thick' (R > 1) and the lower (φ < 0) half is `thin' (R < 1). By decreasing c, the line separating the `thick' and `thin' portions becomes a space curve, thus the thicker portion moves downward and the thinner portion upward. As c approaches zero, the upper half of the body becomes thin and the lower one becomes thick; cf. Figure 4.
		Figure 3: Plot of the body if c = d = 1/2.

 

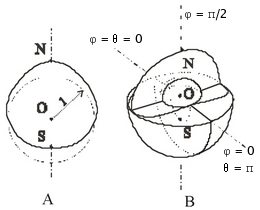Figure 4: A: Side view of the body if \(c \gg 1\) (and d approximately 1/3). Note that ΔR > 0 if φ > 0 and ΔR < 0 if φ < 0. B: Spatial view if \(c \ll 1\). Here, ΔR > 0 typically for φ < 0 and vice versa.

In [12] we proved analytically that there exists ranges for c and d where the body is convex and the center of gravity is at the origin, i.e. it belongs to class {1,1}. Numerical studies suggest that d must be very small (d < 5 × 10^–5 ) to satisfy convexity together with the other restrictions, so the created object is very similar to a sphere. (In the admitted range of d the other parameter c is approximately 0.275.)

4.   What are they not like?

Intuitively, it appears to be clear that mono-monostatic bodies can be neither very flat nor very thin; the former shape would have at least two stable, the latter one at least two unstable equilibria. To make this intuition more exact we define the flatness F and thinness T of a body. Draw a closed curve c on the surface, traced by the position vector R(s), s in [0, 1], from the center of gravity O. Pick two points P_i (i = 1, 2) on opposite sides of c, with position vectors R_i (i = 1, 2), respectively. We define the flatness and thinness as

Although F and T are hard to compute for a general case, it is easy to give both a problem-specific and a general lower bound. For the latter we have

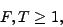(7)

since F = T = 1 can always be obtained by shrinking the curve c to a single point. For 'simple' objects F and T can be determined and the values agree fairly well with intuition:

Table 1: The flatness and thinness of some 'simple' objects.

Body Flatness F Thinness T Sphere 1 1 Regular tetrahedron \(\sqrt{3}\) \(\sqrt{3}\) Cube \(\sqrt{2}\) \(\sqrt{3/2}\) Octahedron \(\sqrt{3/2}\) \(\sqrt{2}\) Cylinder with radius r, height 2h, \(z= \sqrt{r^2 + h^2}\) z/h z/r Ellipsoid with axes a < b < c> b/a c/b

Now we show that F and T are related to the number S of stable and U of unstable equilibria by

Lemma 1	a)	F = 1 if, and only if, S = 1 and
	b)	T = 1 if, and only if, U = 1.

We only prove a), the proof of b) runs analogously. If S > 1 then there exists one global minimum for the radius R and at least one additional (local) minimum. Select c as a closed R = R₀ = constant curve, circling the local minimum very closely. Select the points P₁ and P₂ coinciding with global and local minima, respectively. Now we have \(R_1 \leq R_2 < R_0\) and min(R(s)) = R₀, max(R(s)) = R₂, so S > 1 implies F > 1.

If S = 1 then R has only one minimum, so it assumes only values greater or equal than min(R(s)) on one side of the curve c, so F is less than or equal to 1, but due to (7) we have F = 1.

Q.e.d.

Lemma 1 confirms our initial intuition that mono-monostatic bodies can be neither flat, nor thin. In fact, they have simultaneously 'minimal' flatness and 'minimal' thinness; moreover, they are the only nondegenerate bodies having this property.

Another interesting, though somewhat 'negative' feature of mono-monostatic bodies is the apparent lack of any simple polyhedral approximation. As we mentioned before, the existence of monostatic polyhedra with minimal number of faces has been investigated in the mathematical community [4,5,6,9]. One may generalize this problem to the existence of polyhedra in class {i,j}, with minimal number of faces. Intuitively it appears to be evident that polyhedra exist in each class: if we construct a sufficiently fine triangulation on the surface of a smooth body in class {i,j} with vertices at unstable equilibria, edges at saddles and faces at stable equilibria, then the resulting polyhedron may — at sufficiently high mesh density and appropriate mesh ratios — 'inherit' the class of the approximated smooth body. It also appears to be true that if the topological inequalities \(2 i \geq j + 4\) and \(2 j \geq i + 4\) are valid then we can have 'minimal' polyhedra, where the number of stable equilibria equals the number of faces, the number of unstable equilibria equals the number of vertices and the number of saddles equals the number of edges. Much more puzzling appear to be the polyhedra in classes not satisfying the above topological inequalities: a special case of these polyhedra are monostatic ones, however, many other types belong here as well. In particular, it would be of special interest to know the minimal number of faces of a polyhedron in class {1,1}. We can imagine such a polyhedron as an approximation of a smooth mono-monostatic body. Since the latter are close to the sphere (they are neither flat nor thin), the number of equilibria is particularly sensitive to perturbations, so the minimal number of faces of a mono-monostatic polyhedron may be a very large number.

5.   Mono-monostatic bodies do exist

Arnold's conjecture proved to be correct: there exist homogeneous, convex bodies with just two equilibria; we called these objects mono-monostatic.

Based on the results presented so far, one gets invariably the impression that mono-monostatic bodies are hiding, i.e., they are hard to visualize, hard to describe and hard to identify. In particular, we showed that their form is not similar to any typical representative of any other equilibrium class. We also showed that they are neither flat, nor thin; in fact, they are the only nondegenerate objects having simultaneously minimal flatness and thinness. Imagining their polyhedral approximation seems to be a futile effort as well: the minimal number of faces for mono-monostatic polyhedra might be very large. The extreme physical fragility of these forms (i.e. their sensitivity to local perturbations due to abrasion) was also confirmed by statistical experiments on pebbles (reported in [12]); in a sample of 2000 pebbles not a single mono-monostatic object could be identified. Apparently, mono-monostatic bodies seem to escape everyday human intuition.

Figure 5: Mono-monostatic body (the Gömböc) and Indian Star Tortoise (Geochelone Elegans).

They certainly did not escape Arnold's intuition. Neither does Nature seem to ignore these mysterious objects: being monostatic can be a life-saving property for land animals with a hard shell, e.g. beetles and turtles. In fact, the 'righting response' (i.e., their ability to turn back when placed upside down) of these animals is often regarded as a measure of their ecological fitness ([8,10]). Although the example presented in Section 2 proved to be practically indistinguishable from the sphere, rather different forms are also included in the mono-monostatic class. In particular, we identified one of these forms, which not only shows substantial deviation from the sphere, it also displays remarkable similarity to some turtles and beetles; we named this object the Gömböc. We built the Gömböc by using 3D printing technology and in Figure 5 it can be visually compared to an Indian Star Tortoise (Geochelone Elegans).

Needless to say, the analogy is incomplete, turtles are neither homogeneous nor mono-monostatic. (They do not need to be exactly mono-monostatic; righting is assisted dynamically by the motion of the limbs.) On the other hand, being that close to a mono-monostatic form is probably not just a coincidence; as we indicated before, such forms are unlikely to be found by chance, either by men or by Evolution itself.

Acknowledgement

The support of OTKA grant TS49885 is gratefully acknowledged.

Bibliography

1.	V.I. Arnol'd, Ordinary Differential Equations, 10th printing, MIT Press (1998).
2.	V.I. Arnol'd, Arnold's problems, Springer, Berlin-Heidelberg-New York & PHASIS, Moscow (2005).
3.	M. Berger and B. Gostiaux, Differential Geometry: Manifolds, Curves and Surfaces, Springer, New York (1988).
4.	J.H. Conway and R. Guy, "Stability of Polyhedra", SIAM Rev. 11 (1969), 78-82.
5.	R. Dawson, "Monostatic simplexes", Amer. Math. Monthly 92 (1985), 541-646.
6.	R Dawson and W. Finbow, "What shape is a loaded die?" Mathematical Intelligencer 22 (1999), 32-37.
7.	G. Domokos, J. Papadopoulos, and A. Ruina, "Static equilibria of planar, rigid bodies: is there anything new?" J. Elasticity 36 (1994), 59-66.
8.	S. Freedberg, A.L. Stumpf, M.A. Ewert, and C.E. Nelson, "Developmental environment has long-lasting effects on behavioral performance in two turtles with environmental sex determination", Evolutionary Ecology Research 6 (2004), 739-747.
9.	A. Heppes, "A double-tipping tetrahedron", SIAM Rev. 9 (1967), 599-600.
10.	A.C. Steyermark and J.R. Spotila, "Body temperature and maternal identity affect snapping turtle (Chelydra serpentina) righting response", COPEIA 4 (2001), 1050-1057.
11.	S. Tabachnikov, "Review of Arnold's problems", Mathematical Intelligencer (to appear).
12.	P.L. Várkonyi and G. Domokos, "Static equilibria of rigid bodies: dice, pebbles and the Poincaré-Hopf Theorem, J. Nonlinear Science 16 (2006), 251-283.