Michael C. Dallaston, School of Mathematical Sciences, Queensland University of Technology, Brisbane, QLD 4000, Australia.

1. Introduction

This article is about the dynamics exhibited by solutions of the nonlinear partial differential equation (PDE)

\( \frac{\partial h}{\partial t} + \frac{\partial}{\partial x}\left(h^m\frac{\partial^3h}{\partial x^3} + h^n\frac{\partial h}{\partial x}\right) = 0. \)

(1)

For definiteness, (1) is posed with periodic boundary conditions on a length \(L\). We consider positive solutions, as for most values of \(n\) and \(m\), \(h\to 0\) leads to quantities in a solution becoming singular.

The physical applications of equations of the form (1) are numerous. From fluid mechanics, it describes the evolution of a thin viscous sheet (\(m=3\)) or filament in a Hele-Shaw cell (\(m=1\)), where the fourth order term comes from surface tension and the second order term comes from one of a number of destabilising effects that are of interest, for example an intermolecular disjoining pressure (\(n=-1\) usually, although other values are of interest), thermocapillary Marangoni effect (\(n=2\)), or an unfavourable effect of gravity (Rayleigh-Taylor instability) (\(n=3\)) [10, 2]. From a mathematical perspective, (1) is of interest as an archetypal PDE that will demonstrate an interesting range of nonlinear phenomena. It could be considered a higher-order version of the nonlinear diffusion equation

\( \frac{\partial u}{\partial t} = \frac{\partial}{\partial x}\left(u^n\frac{\partial u}{\partial x}\right) \)

where considerable effort has been put in to determining how the exponent (\(n\)) leads to either finite time singularities or long-time existence of solutions [13].

In the case of (1) several different behaviours have been observed in the literature: for example, the model applied to van der Waals rupture (\(m=3, n=-1\)) exhibits a finite-time singularity whereby \(h\) goes to zero [14, 15], while the velocity is unbounded, at a discrete point in space. The model applied to the breakdown of the Benney equation (\(m=3, n=6\)) exhibits a finite-time singularity whereby \(h\) and its derivative both grow to infinity [11, 3]. We refer to these phenomena as finite-time rupture and finite-time blow-up, respectively. For other values, infinite-time rupture, or steady states, have also been predicted [12, 8, 9].

One way to determine what kinds of singular behaviour are feasible in a given parameter regime is to attempt a self-similar ansatz in (1); for example the scaling

\( h(x,t) = (t_0-t)^\alpha f(\xi), \qquad \xi = \frac{x-x_0}{(t_0-t)^\beta} \)

(2)

presumes a finite time singularity at \(x=x_0\) and \(t=t_0\) occurs, and that a similarity solution \(f\) exists, for which at least some solutions will asymptote towards in the neighbourhood of \((x_0, t_0)\). This singularity could be either in the form of a rupture (\(h\to 0\) at \(x_0\)) for \(\alpha < 0\), or a blow-up (\(h\to \infty\) at \(x_0\)) for \(\alpha > 0\). By balancing the three terms in (1) we find the similarity exponents in terms of the equation's exponents \(m\) and \(n\):

\( \alpha = \frac{1}{m-2n}, \qquad \beta = \frac{m-n}{2(m-2n)}. \)

(3)

For the similarity solution to hold asymptotically on a vanishing region in \(x\), we require \(\beta > 0\). If \(\beta < 0\) then an infinite-time singularity is feasible from making the ansatz

\( h = t^{\alpha} f(\xi), \qquad \xi = t^\beta(x-x_0), \qquad t \to \infty, \)

(4)

in which case balancing the terms in (1) gives the same expression (3).

In addition to the above, the fact that (1) is conservative places an additional constraint on blow-up solutions. If (2) is valid near \(t=t_0\), \(x=x_0\) then the total mass in a region near the singularity goes as

\( M = \int_{x_0-\epsilon}^{x_0+\epsilon} h(x,t) \, \mathrm dx \sim (t_0-t)^{\alpha + \beta} \int_{-\infty}^\infty f(\xi)\,\mathrm d\xi, \)

(5)

for any \(\epsilon > 0\), so that \(\alpha + 2\beta \geq 0\) is required.

The considerations above allow us to divide the \((n,m)\) plane into regions where each sort of self-similar behaviour is feasible:

• Self-similar finite time rupture is feasible for \(m>\max\{2n, n\}\) (so that \(\alpha, \beta > 0\));
• Finite-time is blow-up feasible for \(m<\min\{2n, n-2\}\), based on mass conservation and the signs of similarity exponents. Note that it has been proven that finite-time blow-up is impossible for \(m < n-2\) [1]; for also asymptotics near \(m=n-2\) see [3];
• Infinite-time rupture is feasible for \(n < m < 2n\), so that \(\alpha < 0\) and \(\beta < 0\);
• Infinite-time blow-up is feasible for \(2n < m < n-2\), so that \(\alpha > 0\) and \(\beta < 0\), and conservation of mass is observed.

It must be stressed that the corresponding behaviour is not necessarily generic or even possible in these regions, as such a determination requires finding a given similarity solution and determining its stability at any given point in the \((n,m)\) plane. In addition, there are regions not covered by these parameter values, so other behaviours are clearly possible. For example, a solution may evolve to a stable steady state of (1) if it exists. From the work of [8]:

• Periodic marginally stable steady states (eigenvalues nonpositive) of the PDE (1) exist for \(n < m \lesssim m - 0.8\) (steady states are proven to be unstable for \(n < m < n-1\), with the tighter lower bound established from numerical evidence) [8].

The above result does not necessarily imply asymptotic stability, as the possibility of a neutrally stable (zero eigenvalue) direction on which a solution leaves the steady state is possible.

The above regions are depicted in Figure 1.

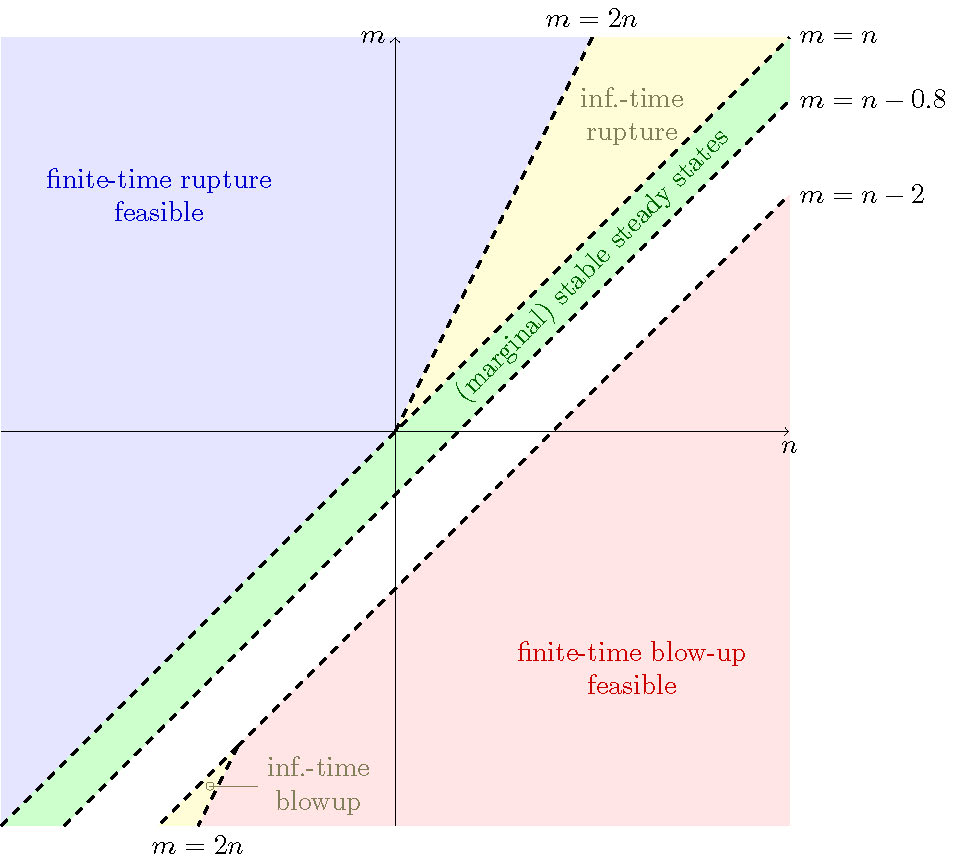
Figure 1: The regions in the \((m,n)\) plane where different kinds of singularities are feasible, according to properties of the similarity exponents (3). The region where stable steady states to (1) may exist is indicated in green [8].

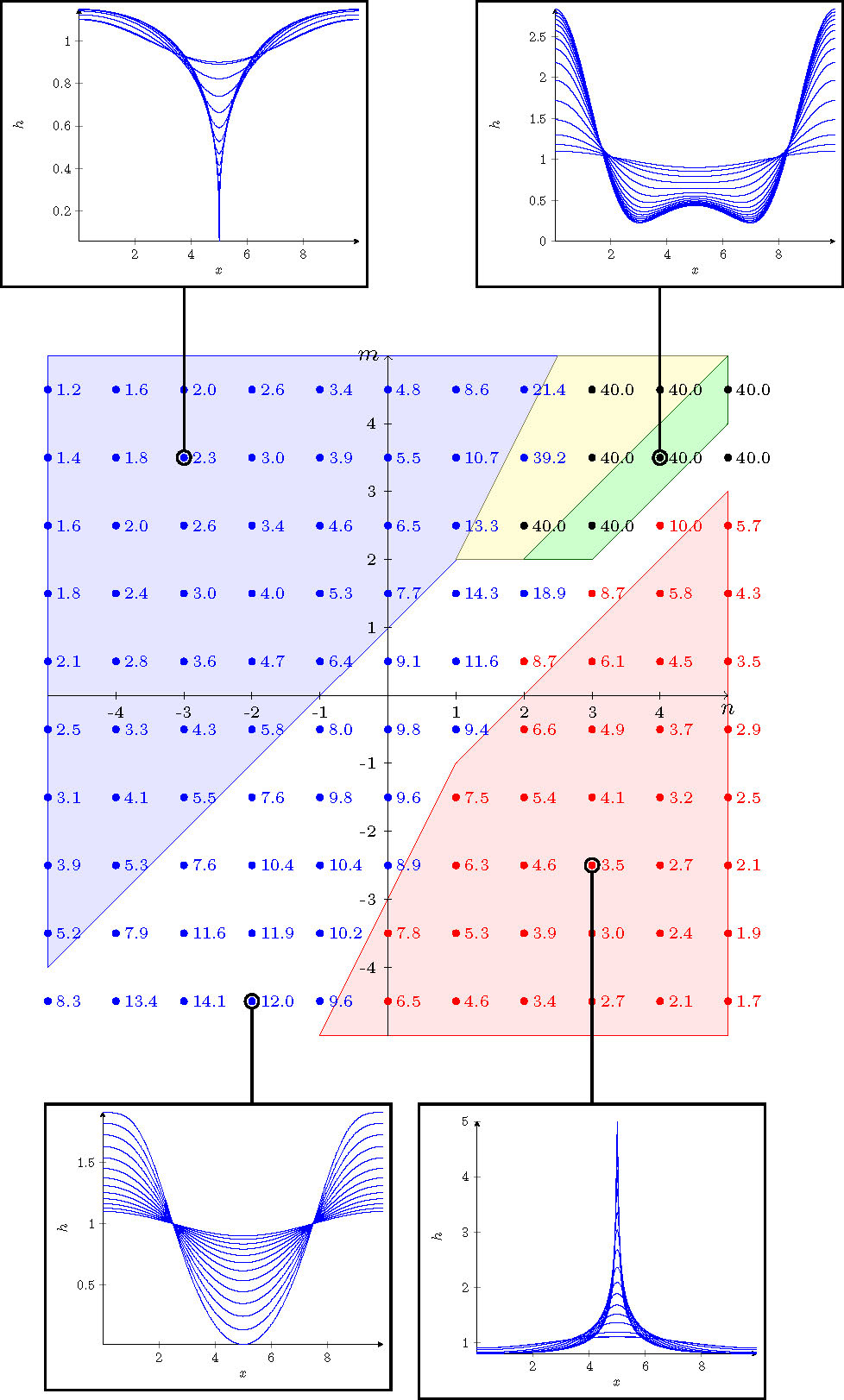
Figure 2: The times for numerical simulations to either reach \(\min h < 0.01\) (blue), or \(\max h > 5\) (red). Solutions that do not reach either of these states by \(t=40\) are in black. Each simulation starts with the initial condition \(h(x,0) = 1 + \cos(2\pi x/L)\) with domain size \(L=10\). Solutions in different regimes are also plotted.

2. Insight from numerical solutions

As a next step to gain insight into the behaviour of (1), we turn to numerical computation. The equation (1) can be solved numerically for various values of \(n\) and \(m\). Here we use a finite volume scheme (see [6] for further details) with \(N=1200\) node points and domain size \(L=10\) Figure 2. The solution is advanced in time using Matlab's ode15s function, an implicit solver which uses adaptive time stepping, and can also take advantage of the sparse structure of a discretised PDE to decrease computational time. We plot the time taken to reach either \(\min h = 0.01\). or \(\max h = 5\), in Figure 2. We also plot some solutions that exhibit some of the different possible behaviours.

By examining the numerical solutions qualitatively, it is apparent there are some regions where finite time rupture, finite time blow-up, infinite-time rupture, and steady states, do occur (there does not seem to be a region where infinite-time rupture occurs). These regions are contained within the predicted regions based on the similarity exponents, but there is another behaviour, which is not exactly self-similar rupture, in which the solution touches down at zero at what appears a finite velocity and a locally parabolic profile. This behaviour occurs in places where finite-time rupture or blow-up, or steady states, might have been supposed to occur based on the similarity exponents alone; note that a similarity solution assumes all three terms in (1) are asymptotically in balance, whereas the expansion \(h \sim A(x-x_0)^2 + \tilde h(x,t)\) would be a valid expansion in (1), near \((x_0, t_0)\), in which \(\tilde h\) is determined from balancing the fourth order term with one of the other two terms. While this topic is still worthy of further investigation, for the remainder of this article we will focus on the finite-time rupture regime, where recent work has shown there is even further complications.

3. Symmetric, asymmetric, and discretely self-similar rupture

In this section we will focus on the region where finite-time rupture is feasible, that is, \(m > \max\{n, 2n\}\), and go into more detail of the calculation of similarity solutions, their stability, and dynamics more generally. Details of this work can be found in [6, 5, 4]. Through numerical continuation and bifurcation, we will see even in the regime of finite-time rupture, a variety of behaviours is possible.

We start by making the ansatz (2); substituting into (1) we find that \(f\) satisfies the ordinary differential equation (ODE)

\( -\alpha f + \beta f' + (f^mf''' + f^nf')' = 0, \)

(6)

With \(\alpha\) and \(\beta\) given by (3). In the finite-time rupture regime, both \(\alpha\) and \(\beta\) are positive.

To fully specify the ODE problem (6), far field conditions are required. The boundary conditions from (1) are not relevant here; due to the scaling (2), a fixed value of \(x>x_0\) corresponds to \(\xi\to\infty\) (and fixed \(x < x_0\) to \(\xi\to-\infty\)). Since the time derivative \(\partial_t h = (t_0-t)^{\alpha-1}(-\alpha f + \beta f')\), the requirement that the time derivative is most singular at the singularity \(x_0\) imposes the condition

\( -\alpha f + \beta f' \to 0 \qquad \Rightarrow \qquad f \sim c_{\pm} |\xi|^{\alpha/\beta}, \qquad \xi \to \pm\infty. \)

(7)

A WKB-style expansion in each far field reveals that two constraints are imposed by each condition, thus the number of boundary conditions is appropriate for the fourth order equation (6). Generally as a fourth order nonlinear equation, (6) can only be solved numerically.

Apart from the desired behaviour (7), the ODE (6) also admits the behaviour \(f \sim c \xi^2\), \(|\xi|\to \infty\). There is therefore also a critical line \(m=n+1\) on which the two far-field behaviours coincide, and the discrete selection of similarity solutions may be lost. As a special case, at \((n,m) = (0,1)\), the equation for the similarity profile (6) is

\( -f + \frac{1}{2}\xi f' = (ff''' + f')' \)

(8)

which has a continuous family of solutions \(f = A(1 + \tfrac{1}{2}\xi^2)\) for any value of \(A\). While further exploration is required, this could be an explanation as to why the line \(m=n+1\) seems to divide the finite-time rupture from non-singular touchdown behaviour in the numerical observations in Figure 2.

To determine the relevance of similarity solutions to the fate of solutions of the original PDE (1), it is valuable to also consider their stability. In order to do this, we must consider similarity solutions as steady states in an appropriate reference frame, or, equivalently, include time-like variable in the similarity ansatz. By defining

\( \tau = -\log(t_0-t), \qquad f = f(\xi, \tau) \)

we obtain a scaled PDE:

\( \frac{\partial f}{\partial\tau} = \alpha f - \beta\xi\frac{\partial f}{\partial \xi} - \frac{\partial}{\partial \xi}\left(f^m\frac{\partial^3 f}{\partial \xi^3} + f^n\frac{\partial f}{\partial\xi}\right), \)

(9)

with appropriate far field conditions

\( \frac{\partial f}{\partial\tau} \sim \alpha f - \beta\xi\frac{\partial f}{\partial \xi}, \qquad |\xi|\to\infty. \)

(10)

In this scaled system, similarity solution (solutions to (6)) are steady states. But we can now ask whether such solutions are stable using the standard methods of linear stability analysis. Writing \(f(\xi,\tau) \sim \bar f(\xi) + \mathrm e^{\sigma \tau} \tilde f(\xi)\), where \(\bar f\) is a similarity solution, and linearising for small \(\tilde f\), we obtain an eigenvalue/eigenfunction problem for \(\sigma\) and \(\tilde f\). This eigenvalue problem must usually be determined numerically (often simultaneously with the computation of \(\bar f\), e.g., [14]). Two eigenpairs that are always present are:

\( \sigma = 1, \qquad \tilde f = -\alpha \bar f + \beta \xi \bar f' \)

(11)

and

\( \sigma = \beta, \qquad \tilde f = \bar f'. \)

(12)

These seemingly unstable directions are the result of the invariance of the original problem (1) with regards to time and space, respectively. They can be seen as perturbations that shift the time and location of the singularity. They thus do not correspond to "true" instabilities of a given similarity solution.

3.1. Computation and numerical continuation

Here we solve (6) as a two point boundary value problem on a domain large enough so that the finiteness of the domain size does not seriously effect the solution. These solutions are computed, and continued in \(m\) and \(n\), with the continuation and bifurcation package AUTO-07p [7].

The bifurcation structure in the finite-time rupture regime is surprisingly complicated. For given \(m\) and sufficiently small \(n\), there are an infinite number of similarity solutions, all symmetric in \(\xi\), but as \(n\) increases, these branches annihilate via fold bifurcations. In Figure 4, the first two branches and their fold bifurcation are show for \(m=3\) and \(m=1.5\) (further branches have been computed in [6]). Here the similarity solutions are characterised by the minimum value \(f_\mathrm{min}\). On this branch there is also a pitchfork bifurcation that leads to asymmetric solutions to (6).

When we consider the stability of these branches, there are further surprises. For sufficiently small \(m\) it is the highest solution branch (that with largest value of \(\min(h)\)) that is linearly stable according to the eigenvalue problem described above. As \(n\) increases there are either one or two Hopf bifurcations (depending on the value of \(m\)), close to the fold, whereby this branch loses its stability. Since the base state \(\bar f\) is symmetric in \(\xi\) at these bifurcations, these Hopf bifurcations may be characterised by the eigenfunction that becomes unstable either being symmetric, or antisymmetric, with respect to \(\xi\). From such bifurcations there exist branches of periodic solutions to the scaled PDE (9). Further details of the numerical challenge of computing these periodic solutions, which are considerable, are to be found in [5, 4]. Finally, for sufficiently small \(m\), the asymmetric solution branch restabilises via another Hopf bifurcation (see Figure 4b).

In Figure 5 we plot the locations of bifurcations in the \((n,m)\) plane. These bifurcations further divide the region of the \((n,m)\) plane where finite-time self-similar rupture is feasible into different kinds of finite-time self-similar rupture, either

• Symmetric, where the profile is asymptotically symmetric around the rupture point \(x_0\);
• Asymmetric, where the profile is not; and
• "Irregular", where solutions to (9) do not settle down to a steady state.

The last of these includes values for which stable periodic orbits to (9) exist. In the context of (9) being a scaled version of the original problem (1), a periodic orbit corresponds to a kind of self-similarity that repeats on discrete scales, rather than on a continuous scale. The challenges of the computation of these orbits mean that it is not settled whether there is always a stable periodic orbit in the irregular regime, or whether there are further bifurcations that could lead to even more complex behaviour, for example, chaotic solutions, as conjectured in [5].

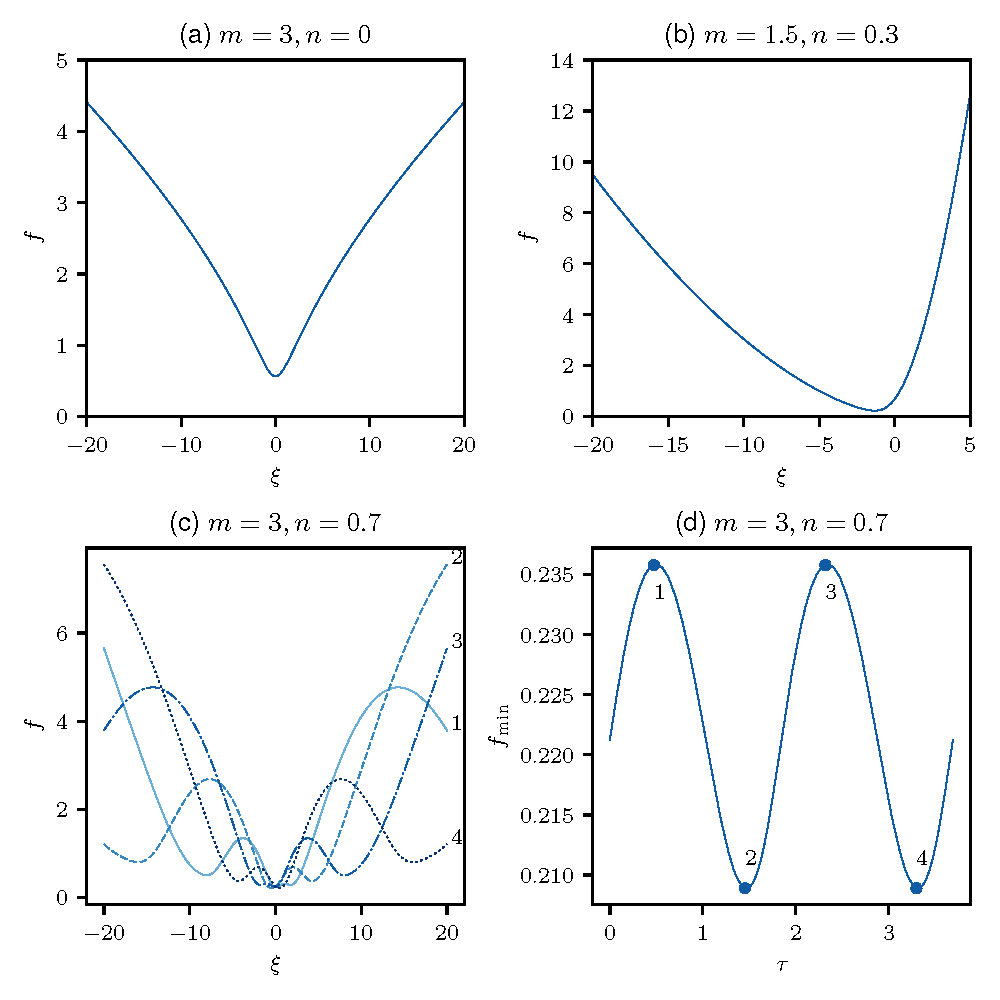
Figure 3: Similarity solutions for (a) the symmetric, and (b) the asymmetric regimes. Frame (c) depicts profiles of a periodic solution to (9), while (d) plots the value of \(\min(f)\) over scaled time \(\tau\) (adapted from [4]).

Figure 4: Bifurcation diagrams for (a) \(m=3\) and (b) \(m=1.5\), depicting the first two symmetric bramches, bifurcations to periodic orbits, and asymmetric similarity solutions (adapted from [4]).

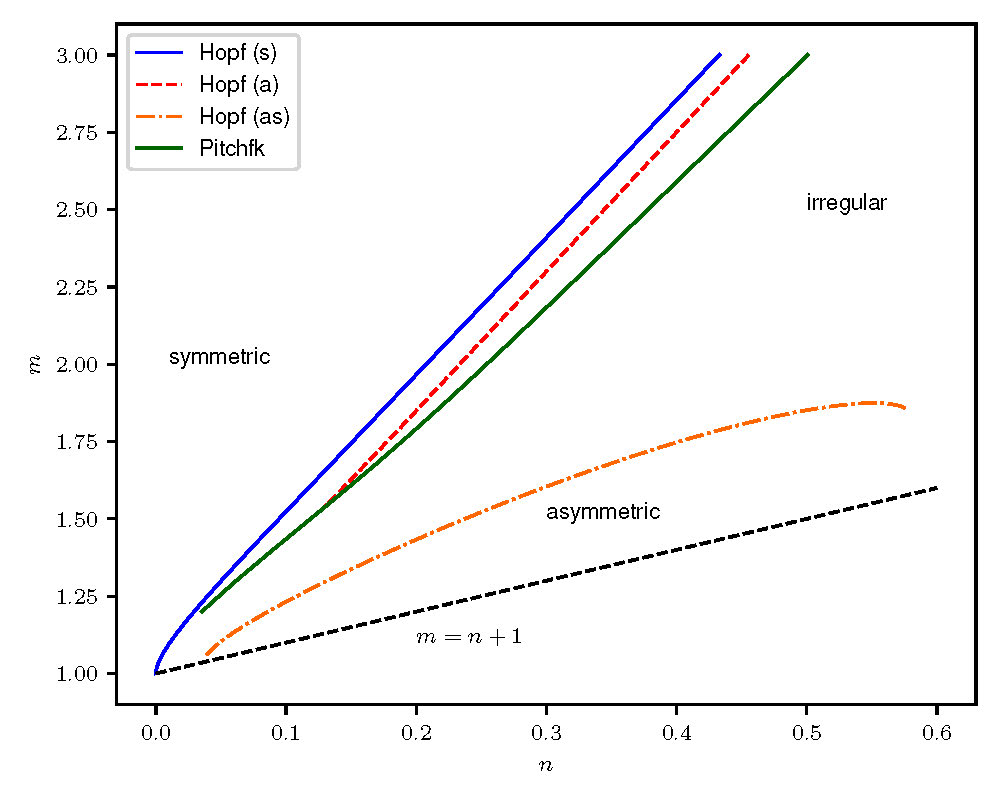
Figure 5: Plots of the locations of bifurcations in the \((n,m)\)-plane, indicated the divide between regimes where symmetric, asymmetric, and irregular self-similar rupture is likely to be observed (adapted from [4]).

4. Unfinished business

While we have discussed in broad terms the very many different sorts of terminal behaviours that the PDE (1) can exhibit, the picture is far from complete and there are many unresolved issues. We discuss a few below. It is clear that even a relatively simple looking PDE (1) inspires many challenges across the range of numerical and analytic studies of partial differential equations.

Hopf-bifurcation structure. A careful look at the twin Hopf bifurcations in Figure 4a suggests that the one that occurs for smaller \(n\) is subcritical, as the branch of periodic orbits curves back into the region where the first similarity solution is stable. In theory the second branch (labelled "antisymmetric branch") of periodic orbits should be unstable, but numerical evidence suggests that these are actually the solutions approached in numerical simulations [5, 4]. Resolution of this requires a detailed examination of the stability of the periodic solution branches, to see if any further bifurcations have been missed.

Critical cases. Examination of the special case \((n,m) = (1,0)\) would be quite illuminating, would the asymptotics of solutions near this point, since it seems to be the meeting point between many different sorts of behaviour.

Rigorous results on rupture. One of the few general results that has been proven is that finite-time blow up is impossible for \(m < n-2\) [1]. No such result is known regarding finite-time rupture. It would be interesting to see whether such results could be established using similar energy methods.

References

[1]   A. L. Bertozzi and M. C. Pugh, Long-wave instabilities and saturation in thin film equations, Commun. Pure Appl. Math., 51(6), 1998, pp 625-661.

[2]   R. V. Craster and O. K. Matar, Dynamics and stability of thin liquid films, Rev. Mod. Phys., 81 (2009), pp. 1131-1198.

[3]   M. C. Dallaston, Matched asymptotic analysis of self-similar blow-up profiles of the thin film equation, Q. J. Mech. Appl. Math., 72 (2019), pp. 179-195.

[4]   M. C. Dallaston, M. A. Fontelos, M. A. Herrada, J. M. Lopez-Herrera, and J. Eggers, Regular and complex singularities of the generalized thin film equation in two dimensions, J. Fluid Mech., 917 (2021), p. A20.

[5]   M. C. Dallaston, M. A. Fontelos, D. Tseluiko, and S. Kalliadasis, Discrete self-similarity in interfacial hydrodynamics and the formation of iterated structures, Phys. Rev. Lett., 120 (2018), p. 034505.

[6]   M. C. Dallaston, D. Tseluiko, Z. Zheng, M. A. Fontelos, and S. Kalliadasis, Self-similar finite-time singularity formation in degenerate parabolic equations arising in thin-film flows, Nonlinearity, 30(7), 2017, p. 2647.

[7]   E. J. Doedel, A. R. Champneys, F. Dercole, T. F. Fairgrieve, Yu. A. Kuznetsov, B. Oldeman, R. C. Paffenroth, B. Sandstede, X. J. Wang, and C. H. Zhang, Auto-07p, Montreal Concordia University, 2007, http://indy.cs.concordia.ca/auto/.

[8]   R. S. Laugesen and M. C. Pugh, Linear stability of steady states for thin film and Cahn-Hilliard type equations, Arch Ration Mech An, 154 (2000), pp. 3-51.

[9]   R. S. Laugesen and M. C. Pugh, Properties of steady states for thin film equations, Eur. J. Appl. Math., 11 (2000), pp. 293-351.

[10]   A. Oron, S. H. Davis, and S. G. Bankoff, Long-scale evolution of thin liquid films, Rev. Mod. Phys., 69 (1997), pp. 931-980.

[11]   A. Pumir, P. Manneville, and Y. Pomeau, On solitary waves running down an inclined plane, J. Fluid Mech., 135 (1983), pp. 27-50.

[12]   S. Shklyaev, A. V. Straube, and A. Pikovsky, Superexponential droplet fractalization as a hierarchical formation of dissipative compactons, Phys. Rev. E, 82 (2010), 020601, pp. 1-4.

[13]   J. L. Vázquez, The porous medium equation: mathematical theory, Oxford University Press, 2007.

[14]   T. P. Witelski and A. J. Bernoff, Stability of self-similar solutions for van der Waals driven thin film rupture, Phys. Fluids, 11(9), 1999, pp. 2443-2445.

[15]   W. W. Zhang and J. R. Lister, Similarity solutions for van der Waals rupture of a thin film on a solid substrate, Phys. Fluids, 9 (1999), pp. 2454-2462.