Editor's note: This article originally appeared in the SIAM News (vol. 43, no. 1, Jan. 2010). We reprint it here with permission of SIAM News and the author.

Also established in 2000 by the SIAM Activity Group on Dynamical Systems, the J.D. Crawford Prize has been awarded every other year since 2001, most recently to Arnd Scheel of the University of Minnesota. Scheel, shown here in Snowbird with Mary Lou Zeeman, was honored “for his transformative work on planar defects, on structures generated by inhomogeneities in oscillatory media, and on stability for almost planar fronts and viscous shocks, and for explaining intriguing experimental results and discovering new patterns in the process.” Created in memory of J.D. Crawford (1954–1998), the prize recognizes recent outstanding work on a topic in nonlinear science; previous recipients are Björn Sandstede, Yannis Kevrekidis, Dwight Barkley, and Andrew Stuart.

The 2009 SIAM Conference on Applications of Dynamical Systems, held in Snowbird, Utah, May 17–21, featured timely sessions on epidemics and climate change, and on mathematical methods from network models, topology, and other areas. Also on the agenda was the awarding of two important SIAG/ DS prizes: the Jürgen Moser Lecture and the J.D. Crawford Prize.

Honored for his contributions to nonlinear science, former SIAM president Martin Golubitsky, director of the Mathematical Biosciences Institute at Ohio State University, gave the 2009 Jürgen Moser Lecture. Arnd Scheel of the University of Minnesota received the J.D. Crawford Prize. Also established in 2000 by the SIAM Activity Group on Dynamical Systems, the J.D. Crawford Prize has been awarded every other year since 2001, most recently to Arnd Scheel of the University of Minnesota. Scheel, shown here in Snowbird with Mary Lou Zeeman, was honored “for his transformative work on planar defects, on structures generated by inhomogeneities in oscillatory media, and on stability for almost planar fronts and viscous shocks, and for explaining intriguing experimental results and discovering new patterns in the process.” Created in memory of J.D. Crawford (1954–1998), the prize recognizes recent outstanding work on a topic in nonlinear science; previous recipients are Björn Sandstede, Yannis Kevrekidis, Dwight Barkley, and Andrew Stuart.

Snowbird, May 2009: Mary Lou Zeeman, chair of the SIAM Activity Group on Dynamical Systems, congratulated 2009 Jürgen Moser Lecturer Martin Golubitsky at the group’s most recent conference. Golubitsky, who titled his lecture “Catastrophes, Symmetry-Breaking, Synchrony-Breaking,” was honored in part “for his seminal contributions to the understanding of dynamics and symmetry.” Established in 2000 in memory of Jürgen Moser (1928–1999), the prize has been awarded every other year beginning in 2001; Golubitsky’s predecessors are Yakov Sinai, David Ruelle, Stephen Smale, and Harry Swinney.

In the Moser Lecture, titled “Catastrophes, Symmetry-Breaking, Synchrony-Breaking,” Golubitsky surveyed the rise, fall, and legacy of catastrophe theory. Misunderstood and exaggerated claims for the catchily named theory emerged in the backlash that followed a media splash in the 1970s. At heart, catastrophe theory is a study of singularities: the various ways in which nonlinearities force geometric objects to kink up, creating discontinuities in their associated dynamics. The French mathematician René Thom (1923–2002) famously showed that there are just seven different kinds of catastrophe, ranging from ordinary folds and cusps to swallowtails and butterflies. But the “menu” of catastrophes and the precise theorems, Golubitsky said, depend on context.

Thom’s theory, developed in the context of potential functions, was limited to systems of co-dimension up to 4 (co-dimension meaning, roughly, the number of free parameters). Other researchers have studied catastrophes in the context of equilibria and dynamics of ODEs. Golubitsky, with David Schaeffer and Ian Stewart, has looked into the theory from the vantage point of “distinguished” parameters and symmetry. In particular, one of the ways in which catastrophes occur is by symmetry-breaking: the seemingly arbitrary choice of one buridan-ian bale of hay over another.

Symmetry-breaking has been investigated extensively, both analytically and experimentally, in Taylor–Couette flow (also called Couette–Taylor flow, depending on which end of the Chunnel one favors), a system made up of a viscous fluid sandwiched between two rotating cylinders. Some of the basic experiments on this system were done by Harry Swinney (the 2007 Moser Lecturer) and co-workers. The pertinent parameters are the ratio a/b of the cylinders’ radii and a pair of Reynolds numbers measuring the velocities of the inner and outer cylinders. At low rotation rates, the fluid does little to call attention to itself. But as things ramp up, a carnival sideshow of spirals, ribbons, vortices, and other asymmetric patterns breaks out. Theorists, including Golubitsky, have explored the abundance of bifurcations produced by Taylor–Couette systems, even predicting features for experimentalists to look for.

Another tantalizing example of pure circular symmetry giving way to rotating and pulsing waves is a combustion experiment in which a gas rises to the surface of a flat circular burner. Beginning in the 1980s, Michael Gorman of the University of Houston and colleagues have studied the patterns that occur, including a phenomenon that’s been dubbed “jumping ponies on a merry-go-round.” Unlike the Navier–Stokes- obeying Taylor–Couette system, Golubitsky pointed out, there is as yet no accurate model for what the flames do. Nevertheless, some of the patterns seen in the flame experiment can be understood through symmetry-breaking bifurcations. In a 2000 paper in the Journal of Nonlinear Science, Golubitsky and colleagues Victor LeBlanc of the University of Ottawa and Ian Melbourne of the University of Surrey (and an invited speaker at the Snowbird meeting) considered patterns associated with quasi-periodic motions stemming from symmetry-breaking bifurcations that occur in flame and fluid systems. (The Gorman flame has symmetry group O(2), which includes a mirror symmetry in addition to purely circular \(SO(2)\) symmetry; Taylor–Couette has symmetry group \(SO(2) \times Z_2\) —or \(SO(2) \times O(2)\), if periodic boundary conditions are assumed; the JNS paper also examined the famous Belousov–Zhabotinsky reaction, whose mathematical idealization has the full two-dimensional euclidean symmetry group \(E(2)\).)

More recently, Golubitsky and his student Maria Leite, now at the University of Oklahoma, have investigated how bifurcations in the dynamics of coupled “cells” depend on the coupling architecture—that is, on the source of the input for each cell. An underlying premise is that the cells are “homogeneous” and “identically coupled.” This means that the dynamics \(x_i\) of cell \(i\) are described by an equation of the form \(x_i = f (x_i, k, other \; \; inputs)\), where \(f\) is the same for all \(i\) (homogeneity) and symmetric under permutations of the \(k\) other inputs (\(k\) being the “valency” of the network). For example, if \(f(x,y,z) = f(x,z,y)\), a three-cell network of valency 2 might have dynamics $$x_1' = f(x_1, x_1, x_2), \\quad x_2' = f(x_2, x_1, x_3), \\quad x_3' = f(x_3, x_1, x_2),$$ which corresponds to network 5 in Figure 1. Any such network obviously allows a synchronous solution \(x_1=x_2=x_3\) satisfying \(x = f(x, x, x)\). The question is, how stable is that solution, and what other possibilities arise as bifurcations? The answer clearly depends in part on the jacobean of \(f\). But it depends just as clearly on the network architecture as well.

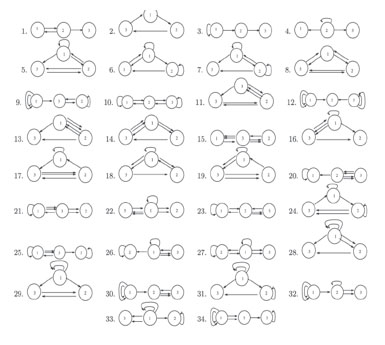
The 34 distinct homogeneous three-cell networks with valency n = 1, 2. From M.C.A. Leite and M. Golubitsky, “Homogeneous three-cell networks,” Nonlinearity, Vol. 19, 2006.

A given network can be represented by a directed graph, with arrows indicating the inputs. In her PhD dissertation, Leite classified the essentially different three-cell networks of valency 1 and 2: There are 34 in all, as shown in Figure 1). (Leite received a Red Sock Award for this work at the 2005 Snowbird meeting.) By contrast, there are only three distinct two-cell networks. The number of networks grows exponentially, or even super-exponentially, with the number of cells (and the valency), Golubitsky says. Nevertheless, he thinks that the implications for dynamics may yet be manageable. In particular, the bifurcations that arise from the network structure are tied to the eigenspace types of the directed graphs’ adjacency matrices. The number of eigenspace types seems to grow at a more leisurely pace, and each type likely has a relatively small number of bifurcations of co-dimension 1.

Even with large numbers of cells, symmetries in the architecture can reduce the analysis to a smaller “quotient” network. Golubitsky, Leite, and a long (and growing) list of colleagues are studying ways in which bifurcations for the quotient networks “lift” to the larger system, along with the possibility of additional bifurcations beyond the lifted ones. Catastrophe theory, it seems, could be on the cusp of a renaissance.

Barry A. Cipra is a mathematician and writer based in Northfield, Minnesota.